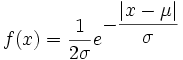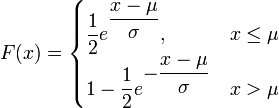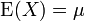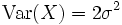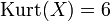Laplaceexperiment

Dichtefunktionen der Laplace-Verteilung für unterschiedliche Parameter

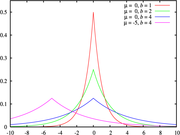
Die Laplace-Verteilung (benannt nach Pierre-Simon Laplace, einem französischen Mathematiker und Astronomen) ist eine stetige Wahrscheinlichkeitsverteilung. Da sie die Form zweier aneinandergefügter Exponentialverteilungen hat, wird sie auch als Doppelexponentialverteilung bezeichnet.

Definition

Eine stetige Zufallsgröße X unterliegt der Laplace-Verteilung mit dem Lageparameter 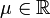$\mu \in \mathbb{R}$ und dem Skalenparameter σ > 0, wenn sie die Wahrscheinlichkeitsdichte

$f(x)= \frac{1}{2\sigma}e^{\displaystyle -\frac{|x-\mu|}{\sigma}}$

besitzt.

Ihre Verteilungsfunktion lautet

$F(x) = \begin{cases}\displaystyle {1 \over 2} e^{\displaystyle\frac{x-\mu}{\sigma}}, & x \leq \mu \\ \displaystyle 1 - {1 \over 2} e^{\displaystyle -\frac{x-\mu}{\sigma}} & x > \mu \end{cases}$

Eigenschaften

Erwartungswert, Median, Modalwert

Der Parameter μ ist Erwartungswert, Median und Modalwert.

$\operatorname{E}(X) = \mu$

Varianz

Die Varianz wird durch den Parameter σ bestimmt.

$\operatorname{Var}(X) = 2 \sigma^2$

Kurtosis

Die Kurtosis einer Laplace-Verteilung ist identisch 6 (entspricht einem Exzess von 3).

$\operatorname{Kurt}(X) = 6$

Charakteristische Funktion

Die charakteristische Funktion hat die Form

$\phi_{X}(s) = \frac{e^{i\mu s}}{1+\sigma^{2}s^{2}}$.

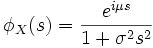Zufallszahlen

Zur Erzeugung doppelexponentialverteilter Zufallszahlen bietet sich die Inversionsmethode an.

Die nach dem Simulationslemma zu bildende Pseudoinverse der Verteilungsfunktion lautet hierbei

$F^{-1}(y) = \begin{cases} \displaystyle {1 \over \lambda} \ln (2 y) & y > {1 \over 2} \\ \displaystyle - {1 \over \lambda} \ln (2 (1 - y)), & y \le {1 \over 2} \end{cases}$.

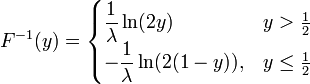Zu einer Folge von Standardzufallszahlen u_i lässt sich daher eine Folge

x_i: = F ^{− 1}(u_i)

doppelexponenzialverteilter Zufallszahlen berechnen.

Beziehung zu anderen Verteilungen

Beziehung zur Normalverteilung

Sind 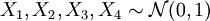$X_1,X_2,X_3,X_4\sim \mathcal N(0,1)$ unabhängige standardnormalverteile Zufallsgrößen dann ist 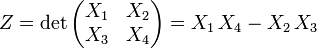$Z=\det\begin{pmatrix} X_1 & X_2 \\ X_3 & X_4 \end{pmatrix}=X_1\, X_4-X_2 \, X_3$ standardlaplaceverteilt.

Beziehung zur Exponentialverteilung

Eine Zufallsvariable X: = Y_λ − Z_λ, die als Differenz zweier unabhängiger und in beiden Fällen exponentialverteilter Zufallsvariablen Y_λ und Z_λ mit demselben Parameter definiert ist, ist Laplace-verteilt.^[1]

Abgrenzung zur stetigen Gleichverteilung

Die so definierte stetige Laplaceverteilung hat nichts mit der stetigen Gleichverteilung zu tun. Sie wird mit ihr trotzdem gerne verwechselt, weil die diskrete Gleichverteilung nach Laplace benannt ist (Laplacewürfel).

Weblinks

• Universität Konstanz - Interaktive Animation

Quellen

1. ↑ Milton Abramowitz und Irene Stegun: Handbook of Mathematical Functions, 1972, S. 930