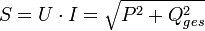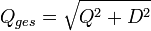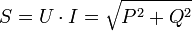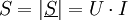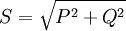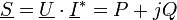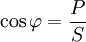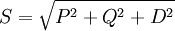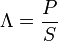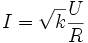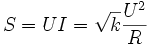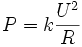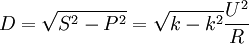- Leistungsdreieck
-
Scheinleistung ist ein Begriff aus der Elektrotechnik. Sie beschreibt jene Leistung, auf welche elektrische Betriebsmittel, die Leistung übertragen, wie Transformatoren oder elektrische Leitungen, ausgelegt sein müssen. Die Scheinleistung S ist die geometrische Summe aus Wirkleistung P und Blindleistung Qges bzw. das Produkt aus den Effektivwerten von Strom I und Spannung U. Die Blindleistung Qges besteht aus Grundschwingungsleistung Q und Verzerrungsblindleistung D.
In Sonderfällen (bei verschwindender Blindleistung), wie beispielsweise bei Gleichspannung, ist die Scheinleistung gleich der Wirkleistung P. Davon abgesehen ist die Scheinleistung im Allgemeinen größer als die Wirkleistung.
Inhaltsverzeichnis
Scheinleistung bei sinusförmigen Größen
Bei sinusförmigen Größen gibt es keine Verzerrungsblindleistung. Deshalb ist die Blindleistung Qges gleich der Grundschwingungsblindleistung Q.
Wenn in einem elektrischen Verbraucher oder einem Versorgungsnetz lineare Induktivitäten oder Kapazitäten zugeschaltet sind, benötigen diese zum Aufbau des magnetischen oder elektrischen Feldes eine elektrische Arbeit, die jedoch mit jeder Halbperiode der Frequenz wieder an das Netz zurückgegeben wird. Der zeitliche Verlauf der Blindleistungswerte ist gegenüber dem der Wirkleistung um eine Viertelperiode (bzw. 90°) verschoben und ergibt komplex (bzw. „geometrisch“) zusammengerechnet mit dieser den Wert der Scheinleistung.
Die Scheinleistung wird gemäß DIN 40110-1 zur Unterscheidung von der Wirkleistung in der Einheit Voltampere (Einheitenzeichen VA) anstelle von Watt (Einheitenzeichen W) angegeben, die Blindleistung in Var (Einheitenzeichen var).
Da neben dem Strom für die Erbringung der Wirkleistung auch der Strom für die Blindleistung aufgebracht werden muss, müssen das Netz und die Betriebsmittel wie z. B. die versorgenden Generatoren und Transformatoren dennoch sämtlich für den Wert der Scheinleistung bemessen werden. Dies gilt nur dann nicht, wenn eine Blindstromkompensation den Blindstrom-Fluss auf die örtlichen verbraucherinternen Leitungsverbindungen begrenzt.
In der komplexen Wechselstromrechnung, welche nur bei eingeschwungenen sinusförmigen Spannungs- bzw. Stromverlauf anwendbar ist, ist die Scheinleistung definiert als Betrag der komplexen Scheinleistung
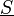 und als geometrische Summe aus Wirkleistung P und Blindleistung Q. Die komplexe Scheinleistung ist definiert als die Multiplikation der komplexen Spannung
und als geometrische Summe aus Wirkleistung P und Blindleistung Q. Die komplexe Scheinleistung ist definiert als die Multiplikation der komplexen Spannung 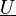 mit dem konjugiert komplexen Strom
mit dem konjugiert komplexen Strom 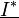 .
.Scheinleistung bei nicht sinusförmigen Größen
Treten in einem elektrischen Netzwerk nicht nur sinusförmige Spannungen und Ströme auf, treten auch sogenannte Oberschwingungen auf. Auch bei nicht stationären Vorgängen, wie beispielsweise Schaltvorgängen, treten nicht sinusförmige Größen auf. Die Scheinleistung muss dann um eine weitere Komponente der Blindleistung, der so genannten Verzerrungsblindleistung D erweitert werden, welche den Anteil der Oberschwingungen an der Blindleistung beschreibt:
Jedes periodische Signal lässt sich mittels der Fourieranalyse in eine Reihe von einzelnen Sinusschwingungen, sogenannten Spektralkomponenten, zerlegen. Zur Berechnung der Scheinleistung im allgemeinen Fall ist daher eine Erweiterung des Begriffes auf beliebig viele Frequenzen notwendig. In diesem Fall lässt sich die Phasenverschiebung zwischen Strom und Spannung nicht mehr einfach mit einem einzigen Winkel
 ausdrücken. An dessen Stelle tritt im allgemeinen Fall der Leistungsfaktor Λ:
ausdrücken. An dessen Stelle tritt im allgemeinen Fall der Leistungsfaktor Λ:Wichtig ist diese Verallgemeinerung immer, wenn nicht auf den Sonderfall reiner Sinusgrößen zurückgegriffen werden kann. Zur Verdeutlichung, wo diese Erweiterung des Begriffes notwendig ist, einige Beispiele dafür:
- Nichtlineare Verbraucher, betrieben an einer sinusförmigen Spannungsquelle. Dies sind beispielsweise Gleichrichter, wie sie in Schaltnetzteilen zu finden sind. Es tritt dabei Verzerrungsblindleistung auf, welche einen Teil der Scheinleistung darstellt.
- Bei der Phasenanschnittsteuerung kommt neben Oberschwingungen und der damit verbundenen Verzerrungsblindleistung zu einer zeitlichen Verschiebung und somit zu einer zusätzlichen Blindleistung in der Grundschwingung – auch bei rein ohmscher Last, welche über eine Phasenanschnittsteuerung in ihrem Leistungsumsatz geregelt wird. Diese Blindleistung wird aufgrund der Ansteuerung mittels Phasenanschnitt Steuerblindleistung genannt, sie ist Teil der Scheinleistung.
- Magnetischen Kreise mit ferromagnetischem Kernmaterial, das nichtlineare Sättigungs- und Hystereseeffekte zeigt − wie z. B. Spulen oder Transformatoren, die daher nichtlineare Induktivitäten darstellen.
- Ein an einer Wechselspannungsquelle mit rechteckigem Signalverlauf betriebener ohmscher Widerstand, wie beispielsweise das Dimmen von Glühlampen mittels Pulsweitenmodulation (PWM).
Steuerblindleistung
Das letzte Beispiel aus obiger Liste soll zwecks Vorstellung der dabei auftretenden Scheinleistung näher erläutert werden: Die Wechselspannungsquelle liefert eine rechteckförmige Spannung fixer Frequenz, d. h. sie schaltet zwischen keiner Spannung und maximaler Spannung an ihrem Ausgang hin und her. Mittels einer Pulsweitenmodulation erfolgt die Leistungsregelung am ohmschen Verbraucher (Glühlampe). Der Pulsbreitenfaktor k im Wertebereich von 0 bis 1 gibt das Verhältnis zwischen der Einschaltzeit der Spannung und der Periodendauer an.
Ist k gleich 1, ist das Pulsbreitenverhältnis maximal: Die Spannung am Ausgang ist eine konstante Gleichspannung. Die abgegebene Wirkleistung ist gleich der Scheinleistung. Ist k gleich 0, ist das Pulsbreitenverhältnis minimal, in diesem Fall ist die Spannung am Ausgang 0 und sowohl abgegebene Scheinleistung wie auch Wirkleistung sind gleich 0.
Für alle anderen Werte von k zwischen 0 und 1 weicht der Betrag der von der Quelle abgegebenen Scheinleistung von der Wirkleistung der Glühlampe ab. Der effektive Strom, den die PWM-Spannungsquelle mit der effektiven Spannung U am Widerstand R der Glühlampe liefert, ist:
Dies eingesetzt in die Definition für die von der Quelle abgegebene Scheinleistung ergibt:
Die Wirkleistung an dem Wirkwiderstand R der Glühlampe mit dem Pulsbreitenfaktor k hingegen ist:
Der vektorielle Differenzbetrag ist Verzerrungsblindleistung D mit dem Betrag:
Bei einem Pulsbreitenverhältnis der PWM von k=0,5 sind Blindleistungsanteil und Wirkleistungsanteil betragsmäßig gleich groß. Die abgegebene Scheinleistung S der PWM-Spannungsquelle beträgt dann das
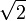 -fache der an der Glühlampe wirksamen Wirkleistung P.
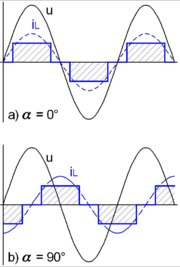
-fache der an der Glühlampe wirksamen Wirkleistung P.Als ein weiteres Beispiel für das Auftreten der Steuerblindleistung sind steuerbare Gleichrichter mittels Phasenanschnittsteuerung am sinusförmigen Wechselspannungsnetz. Auch bei rein ohmscher Belastung auf der Gleichstromseite kommt es auf der Wechselspannungsseite zu einer ohmsch-induktiven Rückwirkung auf das Versorgungsnetz, wie nebenstehende Abbildung zeigt.
Dabei stellt der blau dick dargestellte Stromverlauf den Strom auf der Wechselspannungsseite dar. Der Strom ist abschnittsweise konstant, da er direkt dem Strom auf der Gleichspannungsseite bei konstanter Gleichspannung an einer konstanten ohmschen Last entspricht. Die zu diesem Stromverlauf gehörende Grundschwingung ist dünn blau strichliert eingezeichnet. Man erkennt in der Abbildung, dass die Grundschwingung des Stromes bei der Anschnittststeuerung phasenverschoben wird und somit auf Wechselspannungsseite eine Blindleistung auftritt.
Die von dem Versorgungsnetz zur Verfügung gestellte Scheinleistung auf Wechselspannungsseite ist wie bei der Pulsbreitenmodultion (PWM) betragsmässig unterschiedlich der Wirkleistung auf der Gleichspannungsseite. Diese Differenz wird auch als Steuerblindleistung bezeichnet. Wobei zu beachten ist, dass dieser Begriff in der Literatur nicht einheitlich verwendet wird und festgestellt werden muss ob dabei nur die Blindleistung in der Grundschwingung oder auch die Verzerrungsblindleistung in den Oberschwingungen gemeint sind.
Weitere Verallgemeinerung
Die Verallgemeinerung kann auch noch weiter betrieben werden. Auch Arbeitsfrequenzen unterhalb der Netzfrequenz (z. B. Periodengruppensteuerungen, Vollwellensteuerung) führen zu Verzerrungsblindleistung (auch Modulationsblindleistung genannt) und Subharmonischen. Man kann soweit gehen, dass man bei einem Pumpspeicherkraftwerk, bei dem, von den Verlusten abgesehen, die mittlere Leistung null ist, von Blind- und Scheinleistung spricht (Phasenschieberbetrieb). Berücksichtigt man in Gleichspannungskreisen, dass bei pulsierenden Strömen der Effektivwert des Stromes und sein Mittelwert ungleich sind, so folgt daraus, dass das Produkt aus der Gleichspannung und dem Effektivwert des Stromes eine Scheinleistung (aber :
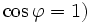 ist.
ist.Siehe auch
Scheinstrom, Scheinwiderstand, Wirkwiderstand, Blindwiderstand, Kurzschlussleistung
Literaturquellen
- René Flosdorff, Günther Hilgarth: Elektrische Energieverteilung. 8. Auflage. Teubner, 2003, ISBN 3-519-26424-2.
Wikimedia Foundation.