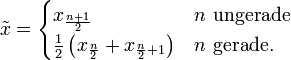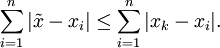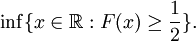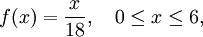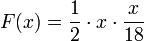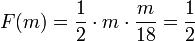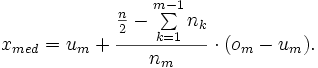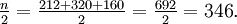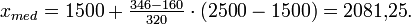Medianeinkommen

Median (oder Zentralwert) bezeichnet eine Grenze zwischen zwei Hälften. In der Statistik halbiert der Median eine Verteilung. Gegenüber dem arithmetischen Mittel, auch Durchschnitt genannt, hat der Median den Vorteil, robuster gegenüber Ausreißern (extrem abweichenden Werten) zu sein und sich auch auf ordinal skalierte Variablen anwenden zu lassen.

Ferner wird in der Geometrie die Seitenhalbierende eines Dreiecks als Median bezeichnet, weil sie das Dreieck in zwei flächengleiche Hälften teilt.

Der Begriff median als anatomische Lagebezeichnung bedeutet in der Mitte liegend oder zur Mitte hin (ausgerichtet oder gelagert).

Median einer Stichprobe

Ein Wert m ist Median einer Stichprobe, wenn höchstens die Hälfte der Beobachtungen in der Stichprobe einen Wert < m und höchstens die Hälfte einen Wert > m hat.

Sortiert man die Beobachtungswerte der Größe nach („geordnete Stichprobe“), so ist der Median bei einer ungeraden Anzahl von Beobachtungen der Wert der in der Mitte dieser Folge liegenden Beobachtung. Bei einer geraden Anzahl von Beobachtungen gibt es kein einziges mittleres Element, sondern zwei. Hier sind die Werte der beiden mittleren Beobachtungen sowie alle Werte dazwischen (obwohl diese bei keiner Beobachtung aufgetreten sind) ein Median der Stichprobe, da für alle diese Werte obige Bedingung zutrifft.

Bei kardinal skalierten Messgrößen (wenn es also sinnvoll möglich ist, die Differenz von Messwerten zu berechnen) verwendet man im Falle einer geraden Anzahl Beobachtungen meist das arithmetische Mittel der beiden mittleren Beobachtungswerte. Der Median 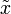$\tilde x$ einer geordneten Stichprobe 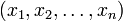$(x_1, x_2, \dots, x_n)$ von n Messwerten ist dann also

$\tilde x =\begin{cases} x_\frac{n+1}{2} &amp;amp;amp; n\text{ ungerade}\\ \frac 12\left(x_{\frac n2} + x_{\frac n2+1}\right) &amp;amp;amp; n \text{ gerade.} \end{cases}$

Oft möchte man dagegen sicherstellen, dass der Median in jedem Fall eines der Elemente der Stichprobe sein soll. In diesem Fall wird alternativ zu dieser Definition bei einer geraden Anzahl von Elementen entweder der Untermedian 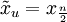$\tilde x_u = x_\frac{n}{2}$ oder der Obermedian 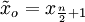$\tilde x_o = x_{\frac{n}{2}+1}$ genutzt und als Median bezeichnet.

Diese Medianbestimmung spielt beispielsweise bei Datenbanksystemen eine große Rolle, wie z. B. bei SELECT-Abfragen mittels des Medians der Mediane.

Eigenschaften

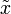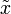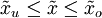Der Median $\tilde x$, und im Fall einer geraden Anzahl von Messwerten alle Werte $\tilde x$ mit $\tilde{x}_u \le \tilde x \le \tilde{x}_o$, minimieren die Summe der absoluten Abweichungen, das heißt für 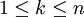$1 \le k \le n$ gilt

$\sum_{i=1}^n |\tilde x - x_i| \le \sum_{i=1}^n |x_k - x_i|.$

Beispiele

• Messwerte 1, 2, 4, 5, 18: ungerade Anzahl. Der Median (auch der Ober- und Untermedian) ist der Wert an der mittleren Stelle, also 4. Das arithmetische Mittel ist 6.
• Messwerte 1, 1, 2, 3, 4, 37: gerade Anzahl. Der Median ist die Hälfte der Summe der beiden mittleren Zahlen, also ½ (2 + 3), also 2,5. Der Obermedian ist 3, und der Untermedian 2. Das arithmetische Mittel ist 8.
• Messwerte 1, 3, 3, 3: gerade Anzahl. Der Median ist ½ (3 + 3), also 3. Der Ober- und der Untermedian sind ebenfalls 3. Das arithmetische Mittel ist 2,5.

Median einer Verteilung

Dichtefunktion einer Dreiecksverteilung mit Median

Eine Verallgemeinerung des Begriffes liefert die stochastische Betrachtung einer Zufallsvariable X bzw. deren Verteilungsfunktion F. Dort ist der Median das 0,5-Quantil, also

$\inf\{x\in\R:F(x) \ge \frac 12\}.$

Übertragen auf die oben genannte Stichprobe wäre nach dieser Definition der Median vergleichbar mit dem dort erwähnten Obermedian.

Er ist, neben beispielsweise Erwartungswert, Modus, ein Lageparameter.

Beispiel

Bei der Dreiecksverteilung

$f(x) = \frac x{18},\quad 0 \le x \le 6,$

ist der Median der x-Wert, welcher die Fläche

$F(x)=\frac 12\cdot x\cdot\frac{x}{18}$

unter der Dichtefunktion in zwei gleich große Flächen teilt. Dieser Wert wird somit durch die Gleichung

$F(m)=\frac 12\cdot m\cdot\frac{m}{18}=\frac 12$

bestimmt. Für deren Lösung 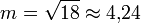$m=\sqrt{18}\approx 4{,}24$ gilt damit $P(X \le 4{,}24) \approx 0{,}5$.

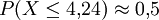D.h. in diesem Beispiel ist der Median m nicht identisch mit dem Erwartungswert E(X) = 4.

Median von gruppierten Daten

Vor allem in den Sozialwissenschaften wird bei Statistiken häufig der Median geschätzt, da nicht alle Daten explizit und exakt gegeben sind, sondern jene nur in Intervallen gruppiert vorliegen. So wird beispielsweise bei Umfragen selten nach dem exakten Gehalt gefragt, sondern nur nach der Einkommensklasse, also dem Bereich, in welchem das Gehalt liegt. Die Berechnungsvorschrift für diese Schätzung unterscheidet sich deswegen von der oben vorgestellten exakten Berechnung des Medians.

Es seien n die Anzahl aller Daten, n_i die jeweilige Anzahl der Daten der i-ten Gruppe und u_i bzw. o_i die entsprechenden oberen bzw. unteren Intervallgrenzen.

Zunächst wird nun die mediane Klasse (oder mediane Gruppe) bestimmt, d. h. diejenige Gruppe, in welche der Median (nach obiger, konventioneller Definition) hineinfällt, z. B. die m-te Gruppe. Wenn keine weiteren Angaben über die Verteilung der Daten gegeben sind, wird z. B. Gleichverteilung postuliert, sodass man sich der linearen Interpolation als Hilfsmittel bedienen kann, um eine Schätzung des Medians der gruppierten Daten zu erhalten:

$x_{med} = u_m+\frac{\frac n2 - \sum\limits_{k=1}^{m-1}n_k}{n_m} \cdot (o_m-u_m).$

Im Gegensatz zur konventionellen Definition des Medians muss dieser nicht zwangsläufig ein Element aus der tatsächlichen Datenmenge sein, welche in aller Regel nicht bekannt ist.

Beispiel

Einkommen:

Klasse (i)	Bereich (ui bis oi)	Gruppengröße (ni)
1	mind. 0, weniger als 1500	160
2	mind. 1500, weniger als 2500	320
3	mind. 2500, weniger als 3500	212

Man berechne

$\textstyle{\frac n2 = \frac{212+320+160}2 = \frac{692}2=346}.$

Also liegt der Median in der 2. Klasse (d. h. m = 2), da die erste Klasse nur 160 Elemente umfasst. Somit ergibt sich als Schätzung für den Median

$\textstyle{x_{med} = 1500+\frac{346-160}{320}\cdot (2500-1500) = 2081{,}25}.$

Eine Veranschaulichung dieses Verfahrens zur Festlegung des Medians bei gruppierten Daten ist die grafische Ermittlung mit Hilfe der Summenkurve. Hier wird der Abszissenwert 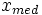$x_{med}\,$ gesucht, der zum Ordinatenwert 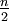$\textstyle{\frac{n}{2}}$ gehört. Bei kleinerem und geradem n kann auch stattdessen der Ordinatenwert 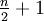$\textstyle{\frac{n}{2}+1}$ gewählt werden.

Vorteile des Medians

Durch seine Resistenz gegen Ausreißer eignet sich der Median besonders gut als Lageparameter für nicht normalverteilte Grundgesamtheiten.

Beispiel:

Die Einkommen einer Gruppe von 10 Personen verteilen sich wie folgt:

• 9 Personen verdienen jeweils EUR 1.000 und
• 1 Person verdient EUR 1.000.000.

Das Durchschnittseinkommen beträgt EUR 100.900, der Median jedoch nur EUR 1.000.

Alternativen

Eine Alternative zum Median bei der Ermittlung des Masseneinkommens aus einer gegebenen Einkommensverteilung ist die von Amartya Sen vorgeschlagene Wohlfahrtsfunktion.

Siehe auch

• Medianalter
• Medianfilter
• Medianwähler

Weblinks

• Ausführliche Erläuterungen zur Berechnung des Medians auf dem „Fußweg“: Wikibooks und Statscan
• Berechnung des Medians in einem Python-Skript (zusammen mit der Berechnung des Gini-Koeffizienten, des Theil-Indexes und der Hoover-Ungleichverteilung)