Dreiecksverteilung

Definition

In der Wahrscheinlichkeitstheorie und Statistik bezeichnet man als Dreiecksverteilung (oder Simpson-Verteilung) eine stetige Wahrscheinlichkeitsverteilung mit der auf dem Intervall $\left[a, b\right]$ definierten Wahrscheinlichkeitsdichtefunktion

$f(x)=\begin{cases} \frac{2(x-a)}{(b-a)(c-a)}, & \text{wenn } a \le x \le c\\ \frac{2(b-x)}{(b-a)(b-c)}, & \text{wenn } c < x \le b. \end{cases}$

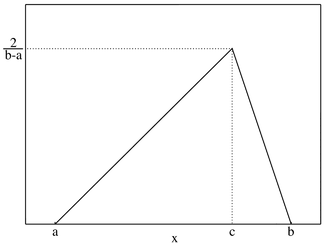
Hierbei bestimmen die Parameter a (minimaler Wert), b (maximaler Wert) und c (wahrscheinlichster Wert) die Gestalt der Dreiecksverteilung $(a\leq c\leq b)$. Die Dichtefunktion sieht wie ein Dreieck aus und gibt dieser Verteilung ihren Namen. Die y-Achse zeigt die jeweilige Wahrscheinlichkeit für einen Wert $x \in \left[a, b\right]$.

Eigenschaften

Verteilungsfunktion

Die Verteilungsfunktion

Die Verteilungsfunktion lautet

$F(x)=\begin{cases} \frac{(x-a)^2}{(b-a)(c-a)}, & \text{wenn } a \le x \le c\\ 1-\frac{(b-x)^2}{(b-a)(b-c)}, & \text{wenn } c < x \le b. \end{cases}$

Die Umkehrfunktion der Verteilungsfunktion lautet

$F^{-1}(y)=\begin{cases} a+\sqrt{y(b-a)(c-a)}, & \text{wenn } 0 \le y \le \frac{(c-a)}{(b-a)}\\ b-\sqrt{(b-a)(b-c)}\sqrt{(1-y)}, & \text{wenn } \frac{(c-a)}{(b-a)} \le y \le 1 \end{cases}$

Erwartungswert

Der Erwartungswert einer dreiecksverteilten Zufallsvariable X lautet

$\operatorname E(X) = \frac{a+b+c}3.$

Varianz

Die Varianz einer dreiecksverteilten Zufallsvariable X ergibt sich zu

$\operatorname{Var}(X) = \frac{a^2+b^2+c^2-ab-ac-bc}{18} = \frac{(a-b)^2+(b-c)^2+(a-c)^2}{36}.$

Beziehung zu anderen Verteilungen

Die Summe zweier identischer unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt mit b − c = c − a, Standardabweichung $\sqrt{6}(b-a)/12=0,204(b-a)$ und mittlerer absoluter Abweichung (b − a) / 6.

Siehe auch

• Thomas Simpson

Weblinks

• Eric W. Weisstein: Triangular Distribution. In: MathWorld. (englisch)
• Universität Konstanz – Interaktive Animation
• Norman L. Johnson, Samuel Kotz: Non-Smooth Sailing or Triangular Distributions Revisited after Some 50 Years. The Statistician, Vol. 48, No. 2 (1999), S. 179–187

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta