4. Dimension

4D oder 4-D (letzteres ist laut Duden die einzige zulässige Form) ist eine verbreitete Abkürzung für vierdimensional als Angabe einer geometrischen Dimension.

Im Gegensatz zum 3D-Raum unserer Vorstellungswelt (Länge-Breite-Höhe, oder x-y-z) bedeutet 4-D, dass ein orthogonales Objekt je 4 Zahlenangaben für seine "Position" und seine "Ausdehnung" benötigt (üblicherweise werden hier die kartesischen Koordinaten x, y, z und w verwendet) sowie vier Winkel, die seine Ausrichtung im Raum bestimmen.

Zur vierten Dimension

Die Einführung solcher mehrdimensionaler „Überräume“, die unserer direkten Erfahrung nicht zugänglich sind, ergibt sich aus Bereichen der Höheren Mathematik bzw. der Physik. Zur Veranschaulichung kann man sich vorstellen, den 3-D-Raum durch eine zusätzliche Dimension auf 4-D zu verallgemeinern – etwa durch eine skalare Eigenschaft (siehe 1D) oder eine Art Farbskala.

Häufig wird die „vierte Dimension“ mit der Zeit gleichgesetzt und der 4-D-Raum mit dem Begriff Raumzeit. Das ist insofern nicht ganz korrekt, als ein solcher Raum nicht euklidisch ist, weil er eine so genannte Raumkrümmung aufweist. Diese entspricht der gedanklichen Übertragung von gekrümmten Flächen (2-D) auf den Raum (3-D). Die Euklidische Geometrie wird erweitert, um gekrümmte Mannigfaltigkeiten mittels Methoden der nicht-euklidischen Geometrie zu beschreiben. Nach Einstein ist es die Anwesenheit von Masse, welche die Raumkrümmung verursacht.

Mathematisch-geometrisch anschauliche Herleitung

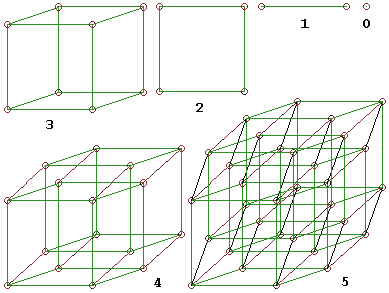
Eine Dimension bezeichnet eine Ausdehnung in eine Richtung, die nicht durch die Richtungen anderer, untergeordneter Dimensionen dargestellt werden kann. Als Beispiel möge der schrittweise Übergang vom Punkt (0D) zu 3-D und 4-D dienen:

Dimension 0

Ein Punkt ohne Ausdehnung (ein Kreis mit Radius 0).

Dimension 1

Wir bewegen uns in einer beliebigen Richtung vom Punkt weg und erhalten eine Strecke. (X-Achse eines Koordinatensystems, Ausdehnung nach links und rechts)

Dimension 2

Wir suchen eine Richtung, die nicht die der Strecke ist, im einfachsten Fall: senkrecht auf die Strecke. Dadurch erhalten wir ein Koordinatensystem, mit welchem wir jeden Punkt einer Ebene erreichen können. (Y-Achse eines Koordinatensystems, Ausdehnung nach vor und zurück).

Dimension 3

Wir suchen eine Richtung, die nicht in der Ebene (aus Dimension 2) liegt. Dazu zeigen wir einmal (vergleichbar dem Sekundenzeiger einer Uhr) in alle Richtungen der Ebene und schließen alle diese Richtungen aus. Zurück bleiben Richtungen, die "nach oben oder unten" zeigen, im einfachsten Fall: senkrecht auf der Ebene "nach oben". Dadurch erhalten wir ein Koordinatensystem, mit welchem wir jeden Punkt im Raum erreichen können. (Z-Achse eines Koordinatensystems, Ausdehnung nach oben und unten).

Dimension 4

Wir suchen wiederum eine Richtung, die nicht im Raum (aus Dimension 3) liegt. Dazu zeigen wir kugelförmig in alle Richtungen, die wir uns vorstellen können und schließen alle diese Richtungen aus. Zurück bleiben Richtungen, die wir uns mit unserem 3-dimensionalen Verstand nicht vorstellen können, im einfachsten Fall: senkrecht auf alle Richtungen, die wir uns vorstellen können. Erweitern wir den Raum in diese Richtung, haben wir einen 4-dimensionalen Hyperraum beschrieben. (W-Achse eines Koordinatensystems, Ausdehnung nach ana und kata, geprägt von Charles Howard Hinton)

Durch derart logische Überlegungen kann man z. B. errechnen, dass ein 4-dimensionaler (Hyper-)Würfel (Tesserakt) 16 Ecken, 32 Kanten, 24 Quadrate und 8 Würfel besitzt.

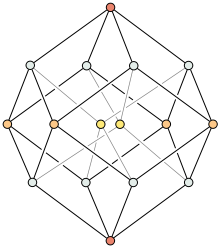
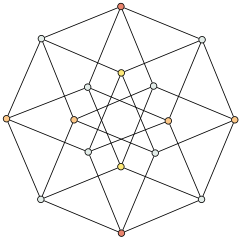
Jede Dimension kann man sich als Zusammensetzung einer unendlichen Anzahl der vorherigen Dimension vorstellen: So kann die Gerade (Dimension 1) als Zusammenfügung einer unendlichen Anzahl Punkte (Dimension 0) gedacht werden. Überträgt man diese Gedanken auf die Vierte Dimension, so kann diese auch als Zusammensetzung unendlich vieler Räume (Dimension 3) gedacht werden.

Die Projektion eines vier-dimensionalen Objekts entsteht im drei-dimensionalen Raum als „Schatten“ stets in 3-D.

Physikalisch verbreitetes Verständnis

Gemäß der obigen mathematischen Definition ist ein 4-dimensionales Koordinatensystem ein Koordinatensystem mit 4 linear unabhängigen Richtungen. Somit eignet es sich, um unsere bekannten 3 Raumdimensionen und die Zeit abzubilden.

In Einsteins Relativitätstheorie sind Raum und Zeit tatsächlich zu einer vierdimensionalen Raumzeit vereinigt. Der Raum zu einem bestimmten Zeitpunkt ist einfach eine Hyperfläche (in der speziellen Relativitätstheorie eine Hyperebene) in der Raumzeit. Damit ist die "Richtung" des Raumes (und der Zeit) in der Raumzeit nicht eindeutig bestimmt. In der Tat hängt die Wahl der Raum-Hyperebene vom Bezugssystem ab. Anschaulich darstellen lässt sich das in Minkowskidiagrammen (siehe auch: Minkowskiraum).

Allerdings ist die Raumzeit – auch die ungekrümmte – nicht euklidisch, da das Quadrat der Zeit mit umgekehrtem Vorzeichen in die Metrik eingeht, weil die Zeit einer imaginären Raumdimension entspricht, was aus der Lorentzinvarianz hervor geht.

Δs² = Δx² + Δy² + Δz² - Δt² * c²

( i * c * t )² = - c² * t²
i = Imaginäre Zahl
i² = - 1
c = Lichtgeschwindigkeit
t = Zeit

Das hat wichtige Folgen, so z. B., dass man nicht einfach in der Zeit umkehren kann.

Aus topologischen Gründen ist für die Einbettung eines gekrümmten 3D-Raumes keine vierte räumliche Dimension erforderlich.

Aus einem 3D-Raum kann auch durch eine andere Dimension als der Zeit ein 4D-Raum entstehen – etwa durch eine zusätzliche skalare Eigenschaft (siehe 1D) oder eine Skala wie der Farbe.

Kosmologische Bedeutung

Inwieweit über unsere Vorstellung hinaus der uns umgebende Raum tatsächlich Ausdehnung in weitere Richtungen hat, damit beschäftigt sich die Kosmologie.

Siehe auch

• Hyperebene
• Hyperwürfel

Weblinks

• http://www.think-strange.de/stuff/projects/vierdimensionale_koerper_im_dreidimensionalen_raum.pdf
• http://cips02.physik.uni-bonn.de/ScienceSite/index.html - Gute, einfache Erklärung und eine 3D-Animation von einem Hypercube
• http://www.4d-screen.de/related-space - Rotierende Körper im Hyperraum - z.B. 4d-plane, kleins bottle und hypercube
• http://www.dimensions-math.org/ Mehrsprachige Erklärungen und Videos zum Thema.