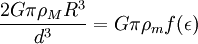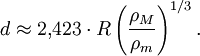- Rochegrenze
-
Die Roche-Grenze ist ein Kriterium zur Beurteilung der inneren Stabilität eines Himmelskörpers, der einen anderen umkreist. Dabei werden die Gravitationskräfte, die den Himmelskörper innerlich zusammenhalten, mit den Gezeitenkräften verglichen, die ihn auseinander ziehen. Die Roche-Grenze ist nach Édouard Albert Roche benannt, der sie 1850 entdeckte.
Ursache der Gezeitenkräfte ist der Umstand, dass die Anziehungskraft durch den Partner auf der ihm zugewandten Seite des Himmelskörpers größer ist als auf der abgewandten. Da der Himmelskörper als Ganzes den Partner umkreist, kommt es zu inneren Spannungen oder Verformungen, die bis zur Auflösung des Himmelskörpers führen können.
Der Begriff Roche-Grenze eines Himmelskörpers wird in zwei verschiedenen Bedeutungen verwendet:
- Als Grenze für seine Umlaufbahn (englisch Roche limit). Bewegt sich der Himmelskörper außerhalb dieser Umlaufbahn, so dominieren die stabilisierenden inneren Gravitationskräfte die Gezeitenkräfte. Diese Bedeutung wird insbesondere verwendet, wenn die Stabilität eines Mondes betrachtet wird, der einen Planeten umkreist.
- Als Grenze für seine geometrische Form (englisch Roche lobe). Befindet sich der Himmelskörper innerhalb dieser Form, so ist er stabil. Diese Bedeutung wird insbesondere verwendet, wenn zwei Sterne einander umkreisen und sich dabei verformen.
Inhaltsverzeichnis
Roche-Grenze als Grenze für die Umlaufbahn
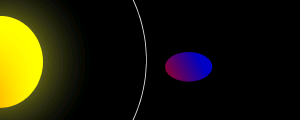
Die Roche-Grenze eines Himmelskörpers, der einen Hauptkörper umkreist, ist die Entfernung, in der der Körper aufgrund der Gezeitenkräfte, die auf ihn wirken, zerrissen wird. Es wird dabei angenommen, dass der Körper nur von den eigenen Gravitationskräften zusammengehalten wird und seine mechanische Festigkeit vernachlässigbar ist. Für reale Festkörper ist diese Annahme um so besser erfüllt, je größer der Körper ist. Daher können künstliche Satelliten problemlos auch innerhalb der Roche-Grenze kreisen, während große Objekte wie Monde und Planeten dort nicht existieren können. Befindet sich Material, das sich noch nicht zu einem Einzelkörper zusammengeballt hat auf einer Umlaufbahn um den Hauptkörper, so wird sich dieses Material innerhalb der Roche-Grenze ringförmig auf dem Orbit verteilen, während es außerhalb der Grenze einen Klumpen bildet.
Tatsächlich befinden sich alle bekannten Planetenringe innerhalb der Roche-Grenze ihrer Planeten. Sie könnten sich daher entweder aus der protoplanetaren Akkretionsscheibe direkt geformt haben, da die Gezeitenkräfte verhindert haben, dass sich Monde aus diesem Material formen, oder Bruchstücke zerstörter Monde sein, die sich von außen über die Roche-Grenze bewegt haben. Alle größeren Monde des Sonnensystems befinden sich dagegen weit außerhalb der Roche-Grenze, kleinere Monde sind jedoch in der Lage sich auch innerhalb der Roche-Grenze aufzuhalten. So befinden sich die Bahnen von Jupiters Mond Metis und Saturns Mond Pan innerhalb der Roche-Grenze für so genannte flüssige Körper. Die mechanische Festigkeit dieser Körper wirkt dabei zum einen direkt gegen die Gezeitenkräfte, die auf den Körper einwirken, und zum anderen bewirkt die Festigkeit auch, dass diese Körper starr bleiben, d. h. ihre Form nicht verändern – ein Effekt der weiter unten beschrieben wird und die Gezeitenkräfte zusätzlich verstärkt. Dieser Effekt wird besonders anschaulich durch die Tatsache beschrieben, dass ein Objekt, das auf die Oberfläche eines solchen Mondes „gelegt“ würde, sich nicht auf dem Mond halten würde, sondern durch die Gezeitenkräfte von der Oberfläche fortgezogen würde. Ein Körper mit geringerer mechanischer Festigkeit, wie beispielsweise ein Komet, würde in diesen Regionen zerstört werden, wie am Beispiel des Kometen Shoemaker-Levy 9 zu sehen war, dessen Orbit im Juli 1992 Jupiters Roche-Grenze durchstieß, woraufhin der Kern des Kometen in zahlreiche Fragmente zerfiel. Bei der nächsten Annäherung an den Planeten im Jahre 1994 schlugen einige dieser Fragmente dann auf dem Planeten ein.
Bestimmung der Roche-Grenze
Die Roche-Grenze hängt von der Verformbarkeit des Satelliten ab, der sich dem Hauptkörper nähert. Zur Berechnung dieser Grenze werden daher zwei extreme Fälle betrachtet. Im ersten Fall, der betrachtet wird, nimmt man an, dass der Körper absolut starr bleibt, bis der Körper von den Gezeitenkräften zerrissen wird. Der gegenteilige Fall, der betrachtet wird, ist ein so genannter „flüssiger Körper“, d. h. ein Satellit, der sich der Verformung überhaupt nicht widersetzt und daher bei der Annäherung an die Roche-Grenze zunächst länglich verformt wird und dann zerreißt. Der zweite Fall liefert erwartungsgemäß den größeren Abstand zum Planeten als Roche-Grenze.
Starre Körper
Beim Fall eines starren Satelliten wird angenommen, dass die inneren Kräfte die Form des Körpers stabil halten, der Körper aber trotzdem nur durch seine Eigengravitation zusammengehalten wird. Weitere Idealisierungen sind die Vernachlässigung eventueller Verformungen des Hauptkörpers durch Gezeitenkräfte oder dessen Eigenrotation, sowie die Eigenrotation des Satelliten. Die Roche-Grenze d ist in diesem Fall
wobei R der Radius des Hauptkörpers, ρM dessen Dichte, und ρm die Dichte des Satelliten beschreibt.
Man bemerkt an der obigen Formel, dass die Roche-Grenze eines starren Körpers für Satelliten, deren Dichte mehr als doppelt so hoch ist wie die Dichte des Hauptkörpers, innerhalb des Hauptkörpers liegt. Dieser Fall tritt z. B. bei vielen felsigen Monden der Gasriesen unseres Sonnensystems auf.
- Herleitung der Formel
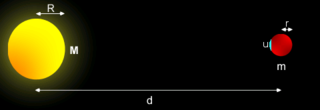
Um die obige Formel herzuleiten, nehmen wir an, dass eine kleine Masse u auf der Oberfläche des Satelliten an dem Punkt liege, der dem Hauptkörper am nächsten ist. Der Satellit selbst wird bei dieser Herangehensweise als sphärisch betrachtet und hat einen Radius r sowie eine Masse m. Auf die kleine Masse u, die auf der Oberfläche liegt, wirken nun zwei Kräfte:
- die Gravitationskraft mit der der Satellit die auf seiner Oberfläche liegende Masse u anzieht:
- die Gezeitenkraft, die auf die Masse u wirkt, da sie vom Hauptkörper angezogen wird, sich aber nicht im Schwerpunkt des Satelliten befindet, der sich im freien Fall (Orbit) um den Hauptkörper bewegt. Im mit dem Satelliten rotierenden Bezugssystem kann man diese Gezeitenkraft auch als Differenz der Gravitationskraft, die vom Hauptkörper auf die Masse u ausgeübt wird, und der Zentrifugalkraft betrachten. Für sie ergibt sich in 1. Näherung
Die Roche-Grenze wird erreicht, wenn der kleine Testkörper auf der Oberfläche des Satelliten anfängt zu schweben, d. h. wenn die Gravitationskraft FG und die Gezeitenkraft FT, den gleichen Betrag annehmen. Für diesen Fall erhält man aus den obigen Gleichungen die Beziehung
die die Testmasse u nicht mehr enthält. Drückt man die Massen der beiden Himmelskörper durch die Dichten ρM und ρm und Radien R und r der entsprechenden Himmelskörper aus, so erhält man die obige von Masse und Radius des Satelliten unabhängige Beziehung.
Flüssige Körper
Das Modell eines flüssigen Satelliten, der den Hauptkörper umkreist, bildet den im Vergleich zu einem starren Satelliten entgegen gesetzten Grenzfall. Flüssig bedeutet dabei, dass der Satellit sich der Verformung durch Gezeitenkräfte überhaupt nicht entgegensetzt. Die Gezeitenkräfte führen dann zu einer länglichen Verformung des Satelliten in Richtung der Verbindungslinie von Satellit und Hauptkörper. Tatsächlich ist dies genau der Effekt, den wir auf der Erde als Gezeiten kennen, bei dem sich die flüssigen Ozeane auf der Oberfläche der Erde in Richtung der Verbindungslinie zum Mond verformen und zwei Flutberge bilden. Da die Stärke der Gezeitenkraft mit der Ausdehnung des Körpers in die Richtung der Verbindungslinie wächst, sorgt eine starke Verformung des Satelliten allerdings für eine noch größere Gezeitenkraft. Daher ist die Roche-Grenze für einen flüssigen Satelliten wesentlich größer, als wir im starren Modell berechnet haben, und zwar:
also ungefähr doppelt so groß wie im starren Modell. Roche hat diese Grenzdistanz bereits um das Jahr 1850 (siehe Literatur) berechnet, wobei er den numerischen Faktor in der Formel mit 2,44 etwas zu hoch ansetzte, was allerdings nicht sonderlich verwundert, da dieser Wert numerisch berechnet werden muss, und dazu im 19. Jahrhundert kein Computer zur Verfügung stand.
Die Roche-Grenze realer Satelliten wird irgendwo zwischen den Grenzen in den beiden extremen Modellen zu erwarten sein und hängt vom Grad der Starrheit des entsprechenden Satelliten ab.
- Herleitung der Formel
Um die oben angegebe Formel herzuleiten, ist wesentlich mehr Aufwand vonnöten als im Falle des starren Körpers. Zunächst müssen wir den Begriff des flüssigen Körpers spezifizieren. Gemeint ist damit ein Körper, der aus einer inkompressiblen Flüssigkeit besteht, die also unabhängig von den äußeren und inneren Kräften eine vorgegebene Dichte ρm und ein vorgegebenes Volumen V besitzt. Weiterhin gehen wir davon aus, dass sich der Satellit in gebundener Rotation auf einer Kreisbahn bewegt, d. h. sein Schwerpunkt ruht in einem mit fester Winkelgeschwindigkeit ω rotierenden Bezugssystem mit Ursprung im Schwerpunkt des Gesamtsystems. Die Winkelgeschwindigkeit ist dabei durch das dritte Kepler'sche Gesetz gegeben:
In diesem Bezugssystem heißt gebundene Rotation des Satelliten, dass sich die Flüssigkeit, aus der der Satellit besteht, nicht bewegt, das Problem kann also als statisch angesehen werden. Daher spielen auch die Viskosität und Reibung der Flüssigkeit in diesem Modell keine Rolle, da diese Größen nur bei Bewegung des Fluids in die Rechnung eingehen würden.
Auf die Flüssigkeit des Satelliten wirken nun im rotierenden Bezugssystem folgende Kräfte:
- Die Gravitationskraft des Hauptkörpers.
- Die Zentrifugalkraft als Scheinkraft im rotierenden Bezugssystem.
- Die Gravitationskraft des Satelliten selbst.
Da alle vorkommenden Kräfte konservativ sind, können sie alle durch ein Potential dargestellt werden. Die Oberfläche des Satelliten nimmt dabei die Form einer Äquipotentialfläche des Gesamtpotentials an, da es andernfalls eine Horizontalkomponente der Kraft an der Oberfläche geben würde, der Teile der Flüssigkeit folgen würden. Welche Form der Satellit bei gegebener Distanz zum Hauptkörper annehmen muss, damit diese Forderung erfüllt ist, soll nun diskutiert werden.
Wir wissen bereits, dass sich die Gravitationskraft des Hauptkörpers und die Zentrifugalkraft im Schwerpunkt des Satelliten aufheben, da dieser sich auf einer (frei fallenden) Kreisbahn bewegt. Die äußere Kraft, die auf die Flüssigkeitspartikel wirkt, ist daher vom Abstand zum Schwerpunkt abhängig und ist die schon im starren Modell benutzte Gezeitenkraft. Für kleine Körper ist der Abstand der Flüssigkeitspartikel vom Schwerpunkt klein gegenüber dem Abstand d zum Hauptkörper und die Gezeitenkraft kann linearisiert werden, wodurch sie die oben angegebene Formel für FT ergibt. Als Abstand vom Schwerpunkt wurde im starren Modell nur der Radius des Satelliten r betrachtet, betrachtet man aber nun einen beliebigen Punkt auf der Oberfläche des Satelliten, so hängt die dort wirksame Gezeitenkraft vom Abstand Δd des Punktes zum Schwerpunkt in radialer Richtung (d. h. parallel zur Verbindungslinie vom Satelliten zum Hauptkörper) ab. Da die Gezeitenkraft linear im radialen Abstand Δd ist, ist ihr Potential in dieser Variable quadratisch ist, und zwar ergibt sich (für
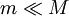 ):
):Wir suchen nun also eine Form für den Satelliten, so dass sich sein Eigengravitationspotential gerade diesem Gezeitenpotential so überlagert, dass das Gesamtpotential auf der Oberfläche konstant wird. Ein solches Problem ist im Allgemeinen sehr schwierig zu lösen, durch die einfache quadratische Abhängigkeit des Gezeitenpotentials vom Abstand vom Schwerpunkt, kann die Lösung dieses Problem aber glücklicherweise durch geschicktes Raten gefunden werden.
Da sich das Gezeitenpotential nur in eine Richtung, nämlich in die Richtung zum Hauptkörper, verändert, ist es naheliegend, dass der Satellit bei seiner Verformung axialsymmetrisch um diese Verbindungslinie bleibt, also einen Rotationskörper bildet. Das Eigenpotential eines solchen Rotationskörpers auf der Oberfläche kann dann nur vom radialen Abstand zum Schwerpunkt abhängen, da die Schnittfläche eines solchen Körpers bei festem radialen Abstand ja gerade eine Kreisscheibe ist, deren Rand sicherlich konstantes Potential besitzt. Sollen nun die summe des Eigenpotentials und des Gezeitenpotentials an jedem Punkt der Oberfläche gleich sein, muss das Eigenpotential genau wie das Gezeitenpotential eine quadratische Abhängigkeit vom radialen Abstand besitzen. Es zeigt sich, dass man dann als Form ein prolates (zigarrenförmiges) Rotationsellipsoid wählen muss. Bei vorgegebener Dichte und Volumen ist das Eigenpotential eines solchen Ellipsoids abhängig von der numerischen Exzentrizität ε des Ellipsoids:
- VS = VS0 + Gπρmf(ε)Δd2,
wobei VS0 das konstante Eigenpotential auf dem kreisförmigen Rand der zentralen Symmetrieebene bei Δd=0 ist. Die dimensionslose Funktion f ist aus der exakten Lösung des Potential eines Rotationsellipsoid zu bestimmen und ergibt sich zu
und hängt erstaunlicherweise nicht vom Volumen des Satelliten ab.
So kompliziert die Abhängigkeit der Funktion f von der Exzentrizität ist, brauchen wir nun dennoch nur noch den geeigneten Wert für die Exzentrizität zu bestimmen, damit VT + VS konstant in der einzigen Ortsvariable Δd ist. Dies ist genau dann der Fall, wenn
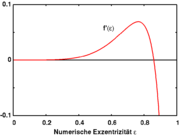
ist, eine Gleichung, die jeder Computer numerisch leicht lösen kann. Wie man am Verlauf der Funktion f in nebenstehender Grafik entnehmen kann, hat diese Gleichung im Allgemeinen zwei Lösungen, wobei die kleinere Lösung, also die geringere Exzentrizität, die stabile Gleichgewichtslage darstellt. Diese Lösung der Gleichung gibt daher die Exzentrizität des Gezeitenellipsoids an, das sich bei einer festgelegten Entfernung zum Hauptkörper einstellt.
Die Roche-Grenze entsteht nun durch die Tatsache, dass die Funktion f, die man als die Stärke der Kraft, die das Ellipsoid in die kugelförmige Gestalt zurückformen will, ansehen kann, nicht beliebig groß werden kann. Es gibt eine gewisse Exzentrizität, bei der diese Kraft maximal wird. Da die Gezeitenkraft aber bei Annäherung an den Hauptkörper über alle Grenzen steigen kann, ist klar, dass es einen Grenzabstand gibt, bei dem das Ellipsoid zerrissen wird.
Die maximale Exzentrizität des Gezeitenellipsoid errechnet man numerisch aus der Nullstelle der Ableitung der Funktion f, die in der Grafik dargestellt ist. Man erhält:
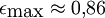 ,
,
was einem Achsenverhältnis von etwa 1:1,95 entspricht. Setzt man diesen Wert in die Funktion f ein, kann man den minimalen Abstand berechnen, in dem ein solches Gezeitenellipsoid existiert – die Roche-Grenze:
Roche-Grenzen ausgewählter Beispiele
Die folgende Tabelle enthält die Dichten und Radien ausgewählter Objekte unseres Sonnensystems.
Objekt Dichte (g/cm3) Radius (km) Sonne 1,400 695.000 Jupiter 1,330 71.500 Erde 5,515 6376,5 Mond 3,340 1737,4 Die oben angegebenen Werte werden nun benutzt, um die Roche-Grenzen für das starre Modell und das flüssige Modell zu berechnen. Als mittlere Dichte eines Kometen wird 500 kg/m3 angenommen. Die wahre Roche-Grenze hängt von der Flexibilität des jeweiligen Satelliten, aber auch von zahlreichen anderen Parametern, wie der Verformung des Hauptkörpers und der genauen Dichteverteilung innerhalb des Satelliten ab und liegt normalerweise zwischen den beiden angegebenen Werten.
Hauptkörper Satellit Roche-Grenze (starr) Roche-Grenze (flüssig) Entfernung
(km)Radius-
quotientEntfernung
(km)Radius-
quotientErde Mond 9.496 1,49 18.261 2,86 Erde Komet 17.883 2,80 34.392 5,39 Sonne Erde 554.441 0,80 1.066.266 1,53 Sonne Jupiter 890.745 1,28 1.713.025 2,46 Sonne Mond 655.323 0,94 1.260.275 1,81 Sonne Komet 1.234.186 1,78 2.373.509 3,42 Man sieht an der obigen Tabelle, dass für besonders dichte Satelliten, die einen weit weniger dichten Hauptkörper umkreisen, die Roche-Grenze innerhalb des Hauptkörpers liegen kann (z. B. beim System Sonne-Erde). In der nächsten Tabelle werden noch einige weitere Beispiele vorgestellt, wobei der tatsächliche Abstand des Satelliten in Prozent der Roche-Grenze angegeben wird. Man sieht z. B., dass der Neptunmond Naiad besonders nahe der Roche-Grenze des starren Modells liegt und daher wohl seiner tatsächlichen physikalischen Roche-Grenze bereits recht nahe ist.
Hauptkörper Satellit Bahnradius vs. Roche-Grenze (starr) (flüssig) Sonne Merkur 10400 % 5400 % Erde Mond 4100 % 2100 % Mars Phobos 172 % 89 % Deimos 451 % 233 % Jupiter Metis 186 % 93 % Adrastea 220 % 110 % Amalthea 228 % 114 % Thebe 260 % 129 % Saturn Pan 174 % 85 % Atlas 182 % 89 % Prometheus 185 % 90 % Pandora 185 % 90 % Epimetheus 198 % 97 % Uranus Cordelia 155 % 79 % Ophelia 167 % 86 % Bianca 184 % 94 % Cressida 192 % 99 % Neptun Naiad 140 % 72 % Thalassa 149 % 77 % Despina 153 % 78 % Galatea 184 % 95 % Larissa 220 % 113 % Pluto Charon 1400 % 720 % Roche-Grenze als geometrische Grenzform
Umkreist ein Stern einen Partner, so wird er durch die Gezeitenkräfte deformiert. Ist der Stern groß und nah genug, so nimmt er eine Tropfenform an mit einer Spitze, die dem Partner zugewandt ist. Befindet er sich in einer Expansionsphase, wie beispielsweise in der Übergangsphase zu einem roten Riesen, so kann er nicht weiter wachsen, sondern es fließt Material über diese Spitze zum Partner. Diese Tropfenform wird ebenfalls als Roche-Grenze bezeichnet. Da dieser Masseverlust die Roche-Grenze verkleinert, kann das ganze System instabil werden, und der Stern komplett zu seinem Partner hinüberfließen.
Handelt es sich bei dem Partner um ein kompaktes Objekt, wie einen weißen Zwerg, einen Neutronenstern oder ein schwarzes Loch, so spielen sich beim Materialtransfer dramatische Prozesse ab. Siehe dazu Novae und Röntgendoppelsterne.
Die Roche-Grenze des Gesamtsystems setzt sich aus den zwei tropfenförmigen Äquipotentialflächen zusammen, die sich an den Spitzen berühren und so die Form einer Acht bilden. Diese Spitze ist der so genannte Lagrange-Punkt L1 des Systems und gleichzeitig der Schwerpunkt. Diese Potentialfläche muss für ein mitrotierendes Koordinatensystem berechnet werden. Es handelt sich um ein effektives Potential, das neben den Gravitationskräften auch die Zentrifugalkräfte berücksichtigt. Sobald sich Material in diesem System bewegt, erfährt es zusätzlich Corioliskräfte, die jedoch nur durch ein geschwindigkeitsabhängiges Potential beschrieben werden können.
Siehe auch
Literatur
- Édouard Roche: La figure d'une masse fluide soumise à l'attraction d'un point éloigné, Acad. des sciences de Montpellier, Vol. 1 (1847-50) p. 243
Weblinks
- Detaillierte Ableitung der Roche-Grenze (allerdings sehr unübersichtlich).
Wikimedia Foundation.





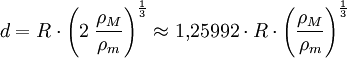
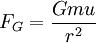
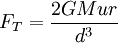
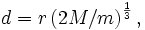
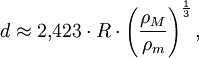
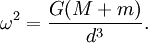

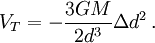
![f(\epsilon)=\epsilon^{-3} (1-\epsilon^2) \cdot \left[ \left(3-\epsilon^2 \right) \cdot \mathrm{arsinh} \left(\frac{\epsilon}{\sqrt{1-\epsilon^2}} \right) -3 \epsilon \right]](/pictures/dewiki/48/015125a012047d640a003f9325fe18db.png)