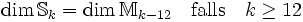- Spitzenform
-
Der klassische Begriff einer Modulform ist der Oberbegriff für eine breite Klasse von Funktionen auf der oberen Halbebene (Elliptische Modulformen) und deren höherdimensionalen Verallgemeinerungen (z. B. Siegelsche Modulformen), der in den mathematischen Teilgebieten der Funktionentheorie und Zahlentheorie betrachtet wird. Der moderne Begriff einer Modulform ist dessen umfassende Neuformulierung in Termen der Darstellungstheorie (automorphe Darstellungen) und arithmetischen Geometrie (p-adische Modulformen). Klassische Modulformen sind Spezialfälle der sogenannten automorphen Formen. Sie zeichnen sich durch mehrere Symmetrie-Eigenschaften aus, das Taniyama-Shimura-Theorem verknüpft sie mit elliptischen Kurven.
Inhaltsverzeichnis
Geschichte
Begründer der klassischen (rein analytischen) Theorie der Modulformen des 19. Jahrhunderts sind Richard Dedekind, Felix Klein, Gotthold Eisenstein und Henri Poincaré. Die moderne Theorie der Modulformen entstand in der ersten Hälfte des zwanzigsten Jahrhunderts durch Erich Hecke und Carl Ludwig Siegel. Modulformen in Termen der Darstellungstheorie stammen von Robert Langlands. p-adische Modulformen treten zuerst bei Nicholas Katz und Jean-Pierre Serre auf.
Elliptische Modulformen für
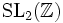
Es sei
die obere Halbebene, d. h. die Menge aller komplexen Zahlen mit positivem Imaginärteil.
Für eine ganze Zahl k heißt eine holomorphe bzw. meromorphe Funktion f auf der oberen Halbebene eine holomorphe bzw. meromorphe elliptische Modulform vom Gewicht k zur Gruppe
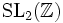 , wenn sie
, wenn sie-
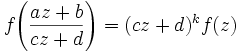 für alle
für alle 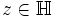 und
und 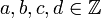 mit ad − bc = 1
mit ad − bc = 1
- erfüllt und
- „holomorph bzw. meromorph im Unendlichen“ ist: Das bedeutet, dass die Funktion
-
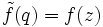 mit
mit 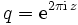 für 0 < | q | < 1
für 0 < | q | < 1
- bei q = 0 holomorph bzw. meromorph auf die Einheitskreisscheibe fortsetzbar ist.
Man beachte, dass aus der ersten Bedingung f(z + 1) = f(z) folgt; deshalb ist
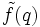 wohldefiniert.
wohldefiniert.Im Falle k = 0 nennt man f eine Modulfunktion.
Ist die Funktion f(z) holomorph im Unendlichen, so heißt f eine ganze Modulform.
Hat darüber hinaus f(z) eine Nullstelle bei
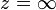 , so nennt man f eine Spitzenform.
, so nennt man f eine Spitzenform.Eigenschaften
Für ungerades k ist stets f = 0, die folgenden Aussagen gelten daher für gerades k.
Die Modulformen vom Gewicht k bilden einen
 -Vektorraum, ebenso die ganzen Modulformen und auch die Spitzenformen.
-Vektorraum, ebenso die ganzen Modulformen und auch die Spitzenformen.Bezeichnet man diese Vektorräume mit
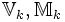 und
und 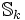 , so gilt:
, so gilt:Für die Dimension dieser Vektorräume gilt:
Da durch die Multiplikation mit der Spitzenform Δ (Diskriminante) vom Gewicht 12 ein Isomorphismus von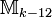 nach
nach 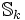 gegeben ist, gilt:
gegeben ist, gilt:Beispiele
Die einfachsten Beispiele für ganze Modulformen vom Gewicht k sind die sogenannten Eisensteinreihen Gk, für eine Modulfunktion die j-Funktion oder absolute Invariante und für eine Spitzenform die Diskriminante Δ.
Veröffentlichungen
- Eberhard Freitag, Rolf Busam: Funktionentheorie 1, 4. Aufl., Springer, Berlin (2006), ISBN 3-540-31764-3
- Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen, 2. Aufl., Springer, Berlin (2007) ISBN 978-3-540-49324-2
Wikimedia Foundation.

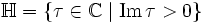
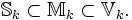
![\mathrm{dim} \, \mathbb{M}_k = \begin{cases} [\frac{k}{12}], &amp; \mathrm{falls} \; k\equiv 2 \; \mathrm{(mod} \, \mathrm{ 12)} \\ \mathrm{[}\frac{k}{12}]+1 &amp; \mathrm{falls} \; k\not\equiv 2 \; \mathrm{(mod} \, \mathrm{ 12)} \end{cases}](/pictures/dewiki/49/106322732b1855b19fa6cf1f11b49d7a.png)