Synthetische Apertur

Ein Synthetic Aperture Radar (Abkürzung: SAR; deutsch etwa: „Radar mit synthetischer Apertur“) gehört ebenso wie ein Real Aperture Radar (Abkürzung: RAR; deutsch: „Radar mit echter Apertur“) zur Klasse der abbildenden Radare. Es wird aus Flugzeugen oder Satelliten eingesetzt und liefert eine 2-dimensionale Darstellung eines Geländeausschnitts durch Abtastung der Erdoberfläche mit elektromagnetischen Wellen.

Die von einem SAR erzeugten Abbildungen sind aufgrund ihrer Ähnlichkeit mit fotografischen Aufnahmen verhältnismäßig leicht interpretierbar und werden für Erderkundungs-, Kartierungs- und Aufklärungszwecke verwendet. Ein SAR ist im Gegensatz zu optischen Sensoren bei nahezu allen Witterungsbedingungen einsatzfähig, da Trübungen der Atmosphäre durch Nebel, Regen oder Schnee die Mikrowellenstrahlung im Vergleich zu Lichtstrahlen weitaus weniger schwächen. Darüber hinaus kann ein SAR, wie jeder aktive Radarsensor, auch bei Nacht eingesetzt werden. Man spricht in dieser Beziehung auch von einem aktiven Fernerkundungssystem, das die beobachteten Objekte selbst beleuchtet.

Während sich die geometrische Auflösung eines RAR wegen des divergierenden Antennenstrahls mit zunehmendem Objektabstand verschlechtert, kann mit einem SAR eine entfernungsunabhängige Ortsauflösung bis herab in den Dezimeterbereich erzielt werden.

Die Synthetische Apertur

RAR-Aufnahmen zur Erzeugung eines SAR-Bildes

Funktionsweise eines SAR

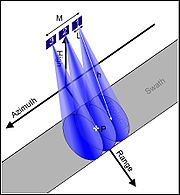
Das SAR-Prinzip erfordert eine senkrecht zur Strahlrichtung bewegte Antenne, deren Position jederzeit exakt bekannt ist. Die Bewegungsrichtung wird üblicherweise als Along Track oder Azimuth (dt.: Flugrichtung oder Azimut) und die Querkoordinate dazu als Cross Track oder Range (dt.: Querrichtung oder Entfernung) bezeichnet. Footprint nennt man den Bereich, den die reale Antenne momentan erfasst, Swath den Geländestreifen, den der Footprint durch die Fortbewegung der realen Antenne überstreicht.

Das Prinzip der synthetischen Apertur besteht darin, die Momentaufnahme einer großen Antenne durch viele mit Hilfe einer kleinen, bewegten Antenne gewonnene Aufnahmen zu ersetzen. Im Verlauf dieser Bewegung wird jedes Objekt im Zielgebiet unter veränderlichem Blickwinkel angestrahlt und entsprechend aufgenommen. Sofern der Weg der realen Antenne hinreichend genau bekannt ist, kann aus Intensität und Phasenlage der empfangenen Radarechos die Apertur einer großen Antenne synthetisiert und so eine hohe Ortsauflösung in Bewegungsrichtung der Antenne erzielt werden.

Mit Hilfe der aufgezeichneten Echodaten wird für jeden von der realen Antenne im Verlauf des Vorbeifluges angestrahlten Ort eine eigene synthetische Antenne berechnet, deren Winkelauflösung im Azimut so gewählt wird, dass für alle betrachteten Entfernungen die geometrische Along Track Auflösung gleich ist.

Dabei ist das folgende Phänomen zu beobachten: Für die gleiche Winkelauflösung benötigt eine synthetische Apertur nur die halbe Länge einer realen Apertur.

Eine anschauliche Erklärung dafür ist: Bei einer realen Apertur beziehen sich Entfernungsänderungen und somit messbare Phasenverschiebungen der Radarechos eines aus Sicht der Antenne parallel vorbei wandernden Objekts immer auf den Ort der Antennenmitte. Bei einer synthetischen Apertur wirken sich zusätzlich die Entfernungs- und Phasenänderungen infolge der nacheinander unterschiedlichen Position der realen Antenne längs der synthetischen Apertur aus.

Damit eine synthetische Apertur realisiert werden kann, ist es zwingend notwendig, dass das Radarsystem voll kohärent arbeitet. Das heißt, die Phasenbeziehung zwischen Sende- und Empfangssignal und von Sendepuls zu Sendepuls muss exakt bekannt sein. Dazu bedient man sich üblicherweise einer hochkonstanten Frequenzquelle von der alle benötigten Misch- und Abtastfrequenzen, sowie alle zeitlich periodischen Vorgänge abgeleitet werden.

Herleitung der geometrischen Auflösung in Azimut

Die mit einem SAR erzielbare bestmögliche Auflösung ist gleich der halben Länge der realen Antenne in Azimut- bzw. Flugrichtung, d.h. bei einer Verkleinerung der azimutalen Antennenlänge L_Az (in der Abbildung oben mit L bezeichnet) der realen Antenne verbessert sich die Auflösefähigkeit δ _Az gemäß :

(1) $\delta_{Az} = \frac{L_{Az}}{2}$

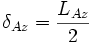
Zur Herleitung sind im Diagramm oben drei Flugpositionen 1, 2 und 3 der in Azimutrichtung bewegten Antenne eingezeichnet. Wie beim RAR beträgt die azimutale Winkelauflösung $\varphi_{Az}$ bei der Wellenlänge λ:

(2) $\varphi_{Az} = \frac{\lambda}{L_{Az}}$'

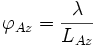Position 2 markiere den Ort des minimalen Abstandes von einem Objekt im Punkt P zur Flugbahn. Ist S₀ die zugehörige Schrägentfernung, dann hat die Achse d_Az der bestrahlten Fläche die Länge:

(3) $d_{Az} = \varphi_{Az} S_0 = \frac{\lambda S_0}{L_{Az}}$

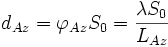
Der Punkt P wird nicht nur von der mittleren Flugposition 2, sondern auch von jeder Position zwischen 1 und 3 bestrahlt. Der Abstand M der Positionen 1 - 3 entspricht somit genau dem Durchmesser d_Az des Antennenleuchtflecks in der fraglichen Entfernung S₀. Das SAR nutzt sämtliche empfangenen Informationen vom Objekt im Punkt P, die von allen Aufnahmen im Bereich M=d_Az stammen. Rechentechnisch wird nach Aufnahme und Speicherung aller Werte eine Antenne mit der azimutalen Länge d_Az simuliert, die gemäß der oben erwähnten Eigenschaft der synthetischen Apertur mit einer gemäß Gl. (3) halbierten Auflösung:

(4) $\delta_{Az} = \frac{\lambda S_0}{2 d_{Az}}$

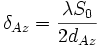
d_Az ist aber aus Gl. (3) bekannt. Ersetzen von d_Az in Gl. (4) führt zu Gl. (1):

(5) $\delta_{Az} = \frac{\lambda S_0}{2} \frac{L_{Az}}{\lambda S_0} = \frac{L_{Az}}{2}$

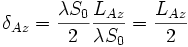
Damit ist die Auflösung der synthetischen Apertur unabhängig von Wellenlänge und Objektentfernung.

Alternative Beschreibung des SAR-Prinzips

Eine andere Beschreibung des SAR-Prinzips liefert die Betrachtung der Doppler-Verschiebung der von einem Objekt reflektierten Echosignale: Beim Eintritt in den Strahlenkegel der Antenne werden die von einem Objekt zurückgeworfenen Echos aufgrund der abnehmenden Entfernung in Richtung höherer Frequenzen verschoben. Nach Passieren des Minimalabstandes (miss distance, genau in Querabposition) vergrößert sich der Abstand wieder und die empfangenen Signale werden zu niedrigeren Frequenzen hin verschoben.

Im Empfänger wird die Mittenfrequenz des Echosignals durch Mischung mit der Mittenfrequenz des Sendesignals auf Null gebracht (Superhet- oder Überlagerungsprinzip). Die verbleibenden Abweichungen von Null bezeichnet man als Dopplerfrequenz oder kurz Doppler. Den Dopplerverlauf der Echos eines Objektes von zunächst positiven Werten durch Null zu negativen Werten nennt man Dopplerhistorie.

Jedes Objekt mit derselben Entfernung zur Flugbahn hat auch dieselbe Dopplerhistorie, allerdings zeitlich verschoben, so wie es der Anordnung längs des Flugwegs und der Fluggeschwindigkeit entspricht.

Objekte in anderen Entfernungen haben dagegen entweder, wenn sie näher liegen, eine zeitlich kürzere oder, wenn sie entfernter liegen, eine längere Dopplerhistorie bei gleichem Frequenzumfang, der als Dopplerbandbreite bezeichnet wird.

Bei nicht zu großem Abstrahlwinkel der realen Antenne kann die Dopplerhistorie als linearer Verlauf der Frequenz über der Zeit angesehen werden; d.h. das auf Null abgemischte Echosignal eines Objektes mit Mittenfrequenz Null stellt ein linear frequenzmoduliertes Signal dar.

Diese als (Down-)Chirp bezeichnete Signalform liegt infolge des gepulsten und kohärenten Sendesignals als Folge von komplexwertigen Einzelwerten vor. Multipliziert man diese Einzelwerte mit korrespondierenden Werten eines gleichartigen Chirps, jedoch mit ansteigender Frequenz (Up-Chirp), so heben sich die den Frequenzänderungen zugrunde liegenden Phasendrehungen auf. Die Addition der resultierenden Einzelwerte liefert nun das Ergebnis der synthetischen Apertur für das speziell betrachtet Objekt.

Diesen Vorgang nennt man Korrelation. Die für jede Entfernung passend zu erzeugende Korrelationsfunktion wird Replika genannt. Sie entspricht im Idealfall den konjugiert komplexen Echowerten eines punktförmigen Zieles.

Während eine angepasste Korrelationsfunktion eine konstruktive Addition aller Einzelbeiträge bewirkt, hat eine nicht angepasste Funktion lediglich ein zufälliges Additionsergebnis zur Folge. Auf diese Weise wird das Echo des betrachteten Objekts, welches gleichzeitig mit den Echos anderer, ebenfalls angestrahlter Objekte am Radarempfänger eintrifft, aus dem Signalgemisch ausgefiltert.

Alternative Herleitung der geometrischen Auflösung in Azimut

Die Radarantenne bewege sich gleichförmig und unbeschleunigt mit der Geschwindigkeit v₀. Wenn $\varphi$ der sich ständig ändernde azimutale Winkel ist, den die Richtung zum Objekt bei P mit der Antennenachse bildet, ist die dem Winkel zugeordnete Dopplerverschiebung des Echosignals dieses Objekts gegeben durch:

(6) $f_D(\varphi) = 2 \frac{v_0}{\lambda} \sin \varphi \approx 2 \frac{v_0}{\lambda} \varphi$

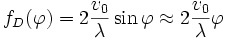
Die Näherung ist für nicht zu große Winkelöffnungen der realen Antenne gültig. Die gesamte Dopplerbandbreite B_D des Echosignals ergibt sich, wenn man die maximal genutzten Azimutwinkel einsetzt und die Werte voneinander subtrahiert:

(7) $B_D = f_D \left ( \frac{\varphi_{Az}}{2} \right ) - f_D \left ( \frac{-\varphi_{Az} }{2} \right ) \approx \frac{v_0}{L_{Az}} - \frac{-v_0}{L_{Az}} = \frac{2 v_0}{L_{Az}}$

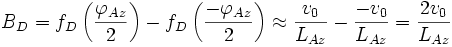
Die Frequenz eines Signals der Dauer T kann bestenfalls mit einer Frequenzauflösung δf = 1/T bestimmt werden. Auf das SAR-Signal angewendet heißt dies, dass die bestmögliche Frequenzauflösung durch die verfügbare Beobachtungszeit bestimmt wird. Diese ist aber gleich der Zeit, die das Radar zum Durchqueren der Strecke M = d_Az benötigt:

(8) $T_{SAR} = \frac{d_{Az}}{v_0} = \frac{\lambda S_0}{v_0 L_{Az}}$

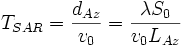
Sie wird als Aperturzeit bezeichnet. Folglich ist die Frequenzauflösung durch:

(9) $\delta f_D = \frac{1}{T_{SAR}} = \frac{v_0 L_{Az}}{\lambda S_0}$

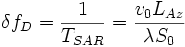
begrenzt. Gemäß Gl. (6) entspricht diese Dopplerfrequenzauflösung einer räumlichen Winkelauflösung von:

(10) $\delta \varphi \approx \frac{\lambda}{2 v_0} \delta f_D = \frac{L_{Az}}{2 S_0}$

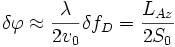
Dies entspricht einem räumlichen Abstand in Azimut von:

(11) $\delta_{Az} = S_0 \delta \varphi = \frac{L_{Az}}{2}$

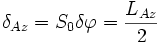
Folglich ist dies die bestmögliche Auflösung eines SAR in Azimut.

Zur Bildung der synthetischen Apertur kann man sich eine Filterbank vorstellen, bei der:

(12) $K = \frac{B_D}{\delta f_D} = 2 \frac{\lambda S_0}{L_{Az}^2} = T_{SAR} B_D$

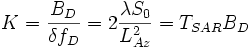
Filter aneinandergereiht die gesamte Dopplerbandbreite abdecken. Die Echos eines Objekts erscheinen, entsprechend ihrer momentanen Dopplerverschiebung, nacheinander am Ausgang eines jeden Filters. Erfasst man diese Signale und addiert sie zeit- und phasenrichtig, so wird das Ergebnis eine K-fach höhere Amplitude aufweisen, verglichen mit einem Signal am Ausgang eines Filters. Die Energie dieses Nutzsignals steigt also auf den K²-fachen Wert, die Energie unerwünschter Signalbestandteile, wie Rauschen oder Echos von Nachbarobjekten dagegen, wegen der zufälligen Natur der Additionen, nur auf das K-fache. Damit verbessert sich der Störabstand (SNR = S/N-Ratio = Signal-to-Noise-Ratio) – das ist das Verhältnis von Nutzenergie zu Störenergie - ebenfalls um das K-fache.

Der Wert K = T_SAR B_D wird als Zeit-Bandbreitenprodukt bezeichnet. Wie man leicht nachrechnen kann, ist die Auflösung gleich der synthetischen Aperturlänge, dividiert durch das Zeit-Bandbreitenprodukt sowie gleich der Fluggeschwindigkeit dividiert durch die Dopplerbandbreite:

(13) $\delta_{Az} = \frac{L_{SAR}}{T_{SAR} B_D} = \frac{v_0 T_{SAR} }{T_{SAR} B_D} = \frac{v_0}{B_D}$

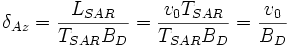
SAR-Beispiel

Um in 10 km Entfernung eine Azimut-Auflösung von 1 m zu erzielen, ist bei einer Verwendung einer realen Antenne eine Aperturlänge von 10 km / 1 m = 10.000 Wellenlängen erforderlich. Bei 10 GHz Sendefrequenz, entsprechend 3 cm Wellenlänge, sind das rund 300 m, also eine praktisch nicht realisierbare Größe. Wie oben erwähnt, braucht eine entsprechende synthetische Apertur nur halb so lang zu sein. Die gleiche Auflösung wird also mit Echodaten bewerkstelligt, die längs einer Strecke von 5 000 Wellenlängen bzw. 150 m aufgezeichnet wurden. Die reale Antenne muss aber sicherstellen, dass das betreffende Objekt während des ganzen Weges angestrahlt werden kann. Dazu ist eine reale Aperturlänge in Azimut von 10 km / 5.000 = 2 m erforderlich.

Das Zeit-Bandbreitenprodukt beträgt nach Gl. (12) dann 2 * 3 cm * 10 km / (2 m * 2 m) = 150, so wie es gemäß Gl. (13) auch sein muss. Bei einer Fluggeschwindigkeit von 100 m/s ist die Dopplerbandbreite 100 Hz, die Aperturzeit 1,5 s und die bestmögliche Frequenzauflösung 0,67 Hz.

Auflösung in Range

Die Bildkoordinate senkrecht zur Flugrichtung (Range) wird ebenso wie beim RAR (auch: Side-Looking-Airborne-Radar,SLAR) durch Entfernungsmessung erzeugt. Diese erfolgt durch Auswertung der unterschiedlichen Signallaufzeiten der Echos verschieden weit entfernter Objekte. Eine solche Messung kann nur in radialer Richtung (= Ausbreitungsrichtung des Sendesignals) erfolgen. Damit eine Bodenfläche in Querrichtung durch eine Entfernungsmessung abgebildet werden kann, muss die Antennenblickrichtung eine seitliche Komponente aufweisen. Somit ist der (auf den Boden projizierte) Flugweg eines SAR immer in einem gewissen Abstand parallel zur nahen Kante des Swath.

Die Auflösung in radialer Richtung (Slant Range) wird grundsätzlich durch die Signalbandbreite des verwendeten Sendesignals bestimmt. Bei steilen Einfallswinkeln verschlechtert sich die erzielbare Range-Auflösung in der Ebene (Ground-Range Resolution) entsprechend der Projektion der radialen Auflösungsstrecke auf den ebenen Boden. Bei 45° Einfallswinkel ist sie daher um den Faktor 1,4 schlechter als in radialer Richtung. Bei senkrechtem Einfall ist eine Entfernungsauflösung in der Ebene nicht mehr definiert.

Wesentliche Elemente eines SAR

Pulskompression

Damit sich eine bildhafte Darstellung des abgeflogenen Geländes ergibt, ist es sinnvoll, die Auflösung in Entfernungsrichtung (Range) vergleichbar zur Azimut-Auflösung zu wählen. Maßgebend für die Range-Auflösung ist die Bandbreite des gesendeten Radarsignals. Für die Auflösung in Richtung der Schrägentfernung (Slant Range) gilt:

(14) $\delta_{Sl} = \frac{c_0}{2 B_R}; c_0 = \frac{300 m}{\mu s} = Lichtgeschwindigkeit$

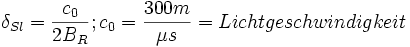
Bei 1 m Auflösung sind also 150 MHz Signalbandbreite erforderlich.

Die Range-Auflösung am Boden wird infolge der Projektion umso stärker herabgesetzt, je steiler der Streifwinkel ε des einfallenden Strahls gegenüber dem Boden ist:

(15) ) $\delta_{Sl} = \frac{c_0}{2 B_R \cos \epsilon}$

Daher wird die Entfernungsauflösung häufig entsprechend feiner als die Azimut-Auflösung gewählt (bei 45° also etwa 70% vom Azimutwert).

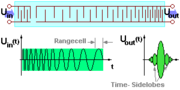
In den ersten Dekaden der Radarentwicklung verwendete man unmodulierte Pulse, d. h. Signale, die z. B. aus einem kontinuierlichen Signal (CW von engl. Continuous Wave) durch kurzes Hochtasten der Senderöhre 'ausgeschnitten' wurden. Ein solches Signal hat eine Bandbreite, die seiner Dauer umgekehrt proportional ist:

(16) $B_{Rect} = \frac{1}{T_{Rect}}$

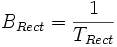
Steigende Auflösungsanforderungen führten demnach zu immer kürzeren Pulsen; den dadurch reduzierten Energieinhalt versuchte man durch immer höhere Sendeleistungen zu kompensieren. Je nach Frequenzbereich konnten 10 MW oder höhere Pulsleistungen realisiert werden. Einer Erhöhung der Pulswiederholfrequenz (PRF, Pulse Repetition Frequency) zur Verbesserung der Energiebilanz stehen häufig andere Gesichtspunkte, wie u.a. die Entfernungseindeutigkeit, entgegen.

Weil sich die Pulsleistung aus technischen Gründen (Spannungsfestigkeit der Bauteile) nicht beliebig steigern lässt, ging man in den 60er Jahren zunehmend zu den Pulskompressionsverfahren über. Hierzu wird ein vergleichsweise langer Puls während der Aussendung in seiner Frequenz geändert. Am häufigsten wird eine lineare Frequenzmodulation (LFM) angewendet, bei der sich die Sendefrequenz linear von einer unteren Grenze bis zu einer oberen Grenze (Up-Chirp) oder umgekehrt (Down-Chirp) ändert. Der Begriff Chirp kommt daher, weil sich ein akustisches LFM-Signal wie Zwitschern anhört. Fledermäuse verwenden übrigens diese Signalform im Ultraschallbereich.

Empfängerseitig wird dieses Signal durch geeignete Verfahren in einen der Bandbreite entsprechenden kurzen Puls verwandelt.

Pulskompression mit einem SAW-Filter

Zu Beginn verwendete man analoge SAW (Surface Acoustic Wave) - Komponenten zur Pulsexpansion und –kompression. Ein kurzer Puls regt eine akustische Oberflächenwelle an, die über ein Substrat mit dispersiven Eigenschaften läuft. Am anderen Ende des Substrates kommen die verschiedenen Frequenzanteile zu unterschiedlichen Zeiten an und bilden so den erwünschten LFM-Puls. Zur Kompression wird ein gleichartiges SAW-Bauteil mit komplementärer Charakteristik verwendet und der gestreckte Puls so wieder zeitlich unter Beibehaltung seiner Bandbreite auf seine ursprüngliche Länge komprimiert.

Seit etwa Mitte der 1980er Jahre die Digitaltechnik in Frequenzbereiche jenseits von 100 MHz vorgestoßen ist, werden praktisch nur noch digitale Signalprozessoren verwendet. Diese verwenden schnelle Digital-Analogwandler, die aus vorher berechneten Daten das Signal – ggf. in mehreren zusammenzusetzenden Frequenzabschnitten – synthetisch erzeugen. Beim Empfang wird das Echo unkomprimiert digitalisiert und die Pulskompression durch ein Korrelationsverfahren im Rechner vorgenommen. Der Vorteil der digitalen Technik liegt darin, dass die Replika für die Kompression unmittelbar aus dem Sendesignal durch Einschleifen in den Empfänger gewonnen werden kann. Die im Sendesignal enthaltenen Abweichungen von der idealen Form, z.B. durch Verzerrungen im Hochfrequenz-Sendeverstärker (HPA von engl. High Power Amplifier), werden somit unmittelbar erfasst. Durch Bildung der konjugiert komplexen Funktion aus den abgetasteten Daten wird die Replika erzeugt. Eine Kompression mit dieser Referenzfunktion entspricht einer Filterung mit einem angepassten Filter (engl. Matched Filter), welches, bei weißem Hintergrundrauschen, das Ausgangssignal mit dem höchstmöglichen Signal/Rausch-Abstand (engl. Signal/Noise-, kurz S/N-Ratio) liefert.

Die Eigenschaften der Pulskompression entsprechen denjenigen des SAR-Signals im Dopplerbereich. So gibt auch hier das Zeit-Bandbreitenprodukt (häufig größer als 1000) den Verkürzungsfaktor für das Chirp-Signal ebenso wie den Gewinn an Störabstand.

Abschließend sei noch bemerkt, dass die für eine bestimmte Auflösung erforderliche Bandbreite auf mehrere Pulse verteilt werden kann (Frequency Step - Verfahren). Dadurch sinken kostspielige Bandbreitenanforderungen an die Radarkomponenten. Gleichzeitig steigt jedoch die Komplexität der radarinternen Steuerung und des SAR-Prozessors.

Antenne

Von den vielen bekannten Antennentypen sind nur drei bei SAR-Anwendungen gebräuchlich:

• Reflektorantenne

Dieser Typ Antenne ähnelt den vielfach verwendeten Satelliten-TV-Empfangsantennen. Die Eigenschaften wie Größe, Bündelungsfähigkeit, Nebenzipfelverhalten u.a. werden unveränderlich beim Entwurf festgelegt. Für eine Schwenkung im Raum (z.B. bei Elevation oder Azimut) muss eine mechanische Drehvorrichtung und/oder mehrere Feed-Elemente vorgesehen werden. Der Vorteil dieses Antennentyps liegt in seiner Eignung für große Bandbreiten bei kostengünstiger Realisierung. Die Reflektorantenne erfordert einen HF-Leistungsverstärker (HPA, High Power Amplifier) als Quelle für das Sendesignal. Die praktisch erforderlichen HF-Leistungen im Bereich von etwa 1 bis 10 kW können gegenwärtig nur durch Röhrenverstärker, meist Wanderfeldröhren (Traveling Wave Tube Amplifier, kurz TWTA) bereitgestellt werden.

• Passive Array-Antenne

Eine Phased Array Antenne setzt sich aus vielen Einzelstrahlern zusammen, die auf einer ebenen Fläche in einem regelmäßigen Raster angeordnet sind. Jeder dieser Strahler oder auch eine Strahlergruppe ist über einen Phasenschieber mit einem Speisenetzwerk verbunden. Die Blickrichtung der Antenne kann durch Änderung der Phasenschiebereinstellungen in einem weiten Bereich (bei Festinstallationen bis zu +/- 60°) elektronisch geschwenkt werden. Der Vorteil ist die praktisch verzögerungsfrei agierende Strahlsteuerung, wie sie bei Multimode-Radargeräten und speziellen SAR-Modi häufig erforderlich ist. Nachteilig sind die im Vergleich zur Reflektorantenne hohen Kosten. Große Schwenkwinkel und hohe Signalbandbreite erfordern spezielle Speisenetzwerke mit in Echtzeit steuerbarer Laufzeit (engl. True Time Delay, kurz TTD), um der Dispersion der Signale zu begegnen. Auch die passive Array-Antenne benötigt eine zentrale Leistungsquelle in Form eines HPA.

• Aktive Array-Antenne

Diese erst in neuerer Zeit realisierbare Antenne ist eine Array-Antenne, bei der jeder Strahler oder kleine Gruppen von Strahlern jeweils einen eigenen Sendeverstärker und ein eigenes Empfangsteil besitzen (Active Electronically Scanned Array). Die Agilität dieses Antennentyps entspricht derjenigen der passiven Array-Antenne, wobei ein zusätzlicher Freiheitsgrad durch selektive Abschaltmöglichkeit einzelner Sendeverstärker hinzukommt. Der hohe Aufwand wird durch einige Vorteile gerechtfertigt. So gestattet die verteilte Erzeugung der Sendeenergie, Halbleiterverstärker mit niedriger Betriebsspannung zu benutzen. Außerdem führt der Ausfall einzelner Verstärker nicht zur Unbrauchbarkeit des Gesamt-Systems (Redundanz).

SAR-Prozessor

Zu Beginn der SAR-Technologie in den 1950 bis 1960er Jahren gab es nur die analoge Signalverarbeitung. Zur Pulskompression benutzte man SAW-Techniken und zur SAR-Fokussierung optische Prozessoren in Form konisch und zylindrisch geschliffener Linsen. Der Nachteil: die Linsen waren nur für eine genau definierte Geometrie bzgl. Höhe und Seitenabstand verwendbar. Mit diesen Verfahren gelang es zwar, Auflösungen im m-Bereich zu realisieren, jedoch führte die fehlende Bewegungskompensation nur in Ausnahmefällen zu optimalen Resultaten.

Erst mit der Einführung schnellerer Rechner und Analog-/Digitalwandler zu Anfang der 1980er Jahre erlebte das SAR-Prinzip den erhofften Durchbruch. Bedingt durch die anfangs kärgliche Rechenleistung suchte man nach rechenzeitsparenden Algorithmen zur SAR-Prozessierung. Das zunächst zur Anwendung gekommene Prinzip war der Range-Doppler-Prozessor, bei dem die Fokussierung in den beiden Koordinaten hauptsächlich durch die schnelle Fourier-Transformation (FFT von engl. Fast Fourier Transformation) erledigt wurden. Diese Prozessoren arbeiteten noch off-line mit Datenaufzeichnung und lieferten die Ergebnisse erst nach der jeweiligen Befliegung. Inzwischen sind weitere Algorithmen (Chirp Scaling, Frequency Scaling u. v. a.) verfügbar. Diese nun erlauben eine echtzeitfähige SAR-Prozessierung auch für sehr spezielle SAR-Modi (s. u.).

Eine SAR-Fokussierung hat nur dann ein gutes Ergebnis zur Folge, wenn der Ort der Antenne weniger als etwa λ/16 von der idealen Flugbahn abweicht. Bei 10 GHz Sendefrequenz sind das weniger als 2 mm! Eine der wichtigsten Aufgaben eines SAR-Prozessors für Systeme im Lufteinsatz ist daher heute die Bewegungskompensation. Dazu werden einerseits die Lage- und Bewegungsdaten hochempfindlicher, GPS-gestützter Kreiselplattformen aufgezeichnet und ausgewertet und zusätzlich Autofokus-Rechenverfahren angewendet, um die unvermeidlichen Abweichungen von einer idealen Flugbahn zu erkennen und zu beseitigen. Autofokusverfahren erfordern ein mehrfaches Berechnen von SAR-Bildausschnitten, um daraus die Bewegungsfehler zu ermitteln. Daher ist die erforderliche Rechenkapazität bei Echtzeitanforderungen erheblich höher als bei Systemen ohne Autofokus-Fähigkeit.

Spezielle SAR-Verfahren

• Spotlight-SAR

Bei diesem SAR-Verfahren wird die Azimut-Auflösung gegenüber der in (1) angegebenen Grenze dadurch verbessert, dass die Antenne für längere Zeit fest auf ein bestimmtes Zielgebiet (Spot) gerichtet bleibt; im Azimut also entsprechend gedreht wird. Dadurch erhöht sich das Zeit-Bandbreitenprodukt und mithin verbessert sich die erzielbare Auflösung. Dies geschieht allerdings auf Kosten der insgesamt abbildbaren Fläche, denn der nächste Spot kann erst in einem durch die Beobachtungszeit und die Fluggeschwindigkeit bestimmten Abstand ins Visier genommen werden.

• Squinted SAR

Ein SAR-Bild kann auch dann erzeugt werden, wenn die Blickrichtung der Antenne nicht querab, sondern schräg nach vorn oder hinten gerichted ist. Die Prozessierung erfordert zusätzliche Algorithmen zur Korrektur der sich nicht rechtwinklig schneidenden Koordinaten Range und Doppler. In Vorausrichtung und unterhalb des Flugweges versagt das SAR-Prinzip aus prinzipiellen Gründen.

• ScanSAR

Hierbei macht man von der Agilität einer passiven oder aktiven Array-Antenne Gebrauch, indem mehrere Streifen in verschiedenen Abständen und Squint-Winkeln quasi gleichzeitig nach einem ausgeklügelten Ablaufplan bedient werden.

• Interferometrisches SAR

Bedingt durch die kohärente SAR-Signalverarbeitung, eignet sich das SAR auch für dreidimensionale Abbildungen. Dazu wird in einer geringen Höhe oberhalb der SAR-Antenne eine zweite Antenne mit komplettem Empfangszug installiert. Die aus beiden Empfängern stammenden komplexen SAR-Bilder unterscheiden sich aufgrund der unterschiedlichen Echo-Laufwege in der Phase. Dieser Phasenunterschied kann zur Bestimmung der Objekthöhen und somit zur Erstellung eines dreidimensionalen Geländemodells genutzt werden.

Das Verfahren funktioniert auch bei Systemen mit nur einer Empfangsantenne. Dazu wertet man die Aufnahme-Daten zweier paraller Flugwege interferometrisch aus (Two-Pass Interferometrie). Wegen des zeitlichen Abstandes beider Aufnahmen werden bewegte Elemente jedoch nicht erfasst.

Bei Vorhandensein eines festen Bezugspunktes lassen sich durch differenzielle Interferometrie exakte Höhen mit Genauigkeiten bis in den mm-Bereich hinein bestimmen.

• Polarimetrisches SAR

Ein polarimetrisches Radar ist in der Lage Wellen unterschiedlicher Polarisierung zu senden und zu empfangen. Aus der Polarisierung der empfangenen Wellen bzw. der Polarisationsänderung lassen sich weitere Informationen über das abgebildete Gelände gewinnen, die zum Beispiel die Unterscheidung zwischen Wald und Häusern erleichtern.

• Inverse SAR (ISAR)

Das ISAR stellt eine Umkehr des klassischen SAR-Prinzips dar: die Radarantenne steht fest und das beobachtete Objekt bewegt sich. Die erzielbare Auflösung wird durch das Zeit-Bandbreitenprodukt der Echosignale bestimmt. Das Verfahren wird z.B. zur Abbildung von Satelliten verwendet. Ferner kann ein im Seegang oder durch eigene Fahrt bewegtes Schiff durch ISAR so abgebildet werden, dass der Schiffstyp erkennbar wird.

• Bi- und multistatisches SAR

Bei bistatischem bzw. multistatischem SAR sind Sender und Empfänger auf zwei bzw. mehreren Trägerplattformen montiert. Somit können mehr Informationen über die Rückstreueigenschaften mit flexibleren Ein- und Ausfallswinkeln gewonnen werden. Eine technische Schwierigkeit ist dabei die Synchronisation der Oszillatoren. Auch müssen bei der Prozessierung neue Verfahren angewendet werden.

Besonderheiten der Abbildung durch SAR

Die mittels SAR gewonnenen Abbildungen weisen einige Besonderheiten auf, die bei der Auswertung berücksichtigt werden müssen:

• Schattenwurf

Bedingt durch die Ausleuchtung mittels mitgeführter "Lichtquelle", weisen die Abbildungen Schatten, also Orte ohne reflektierte Echos, auf. Diese entstehen, wie bei der optischen Abbildung, dort, wo Gebiete durch höhere Objekte vom Radarstrahl abgeschattet werden. Der Effekt ist umso ausgeprägter, je flacher der Streifwinkel und je höher das schattenwerfende Objekt ist. Andererseits erlauben die Schatten auch ein gutes Interpretieren der plastisch wirkenden Abbildungen. Ein Streifwinkel von 5° gilt als untere Grenze für gut auswertbare SAR-Bilder.

• Überlagerung (Lay-Over)

Bei einem hohen Objekt, wie beispielsweise einem Turm, hat die Turmspitze einen geringeren Abstand zum Radar als der Fußpunkt. Die Spitze des Turmes wird früher, also näher, abgebildet. So entsteht der Eindruck eines Überhanges in einem RADAR-Bild. Dies kann bei Abbildungen von gebirgigen Geländen zu Interpretationsschwierigkeiten führen.

• Verkürzung (Foreshortening)

Unter Foreshortening bezeichnet man eine verkürzte Darstellung tatsächlicher Entfernungen (Stauchung von Entfernungen). Man stelle sich einen Kirchturm vor, der von RADAR-Strahlen getroffen wird. Die Basis des Turmes reflektiert zuerst die RADAR-Strahlen, danach die Spitze. Liegen die beiden Zeitpunkte der Reflexion sehr dicht beieinander, wird die tatsächliche Entfernung zwischen Basis und Spitze des Turmes gestaucht wiedergegeben. Wie beim Lay-Over erschwert dieser Effekt die Interpretation einer Gebirgslandschaft.

• Bewegtzielverschiebung

Ein quer zum Flugweg fahrendes Objekt wird am falschen Ort abgebildet. Dies erfolgt deshalb, weil sich zu der Dopplerhistorie eines festen Objekts der Dopplerversatz des bewegten Objekts addiert bzw. subtrahiert. Dies entspricht aber der Historie eines später oder früher angeordneten Objekts. Ein fahrender Zug wird daher neben den Gleisen abgebildet. Die Gleise weisen an der Stelle, wo sich der Zug tatsächlich befand, keine Reflexionen, also eine schwarze Stelle, auf. Ein parallel zur Flugbahn sich bewegendes Objekt verursacht Steigungsänderung der Dopplerhistorie und mithin eine unvollkommene, verschwommene Fokussierung.

• Speckle

Unter Speckle versteht man die Eigenart einer kohärenten Abbildung, dass flächige Objekte, wie z.B. bestellte Äcker, von Bildpunkt zu Bildpunkt, aufgrund der zufälligen Zusammensetzung der Echos aus Einzelbeiträgen, völlig andere Werte annehmen können. Bilder mit Speckle wirken daher zerrissen und körnig. Speckle kann, auf Kosten der Auflösung, durch die Anwendung des Multilook-Verfahrens reduziert werden. Dazu werden mehrere schlechter aufgelöste SAR-Bilder aus unterschiedlichen Dopplerbereichen berechnet und anschließend inkohärent (energiemäßig) addiert. Die zufällige Verteilung der Werte eines Flächen-Bildpunkts sorgt für eine Reduzierung des Speckle.

SAR-Anwendungen

Flugzeug-SAR

Flugzeuggetragene SAR-System werden, aufgrund ihrer Allwetterfähigkeit, vorwiegend für militärische Aufklärung eingesetzt. Die derzeit (2005) technisch erzielbare geometrische Auflösung liegt bei unter 15 cm, was eine HF-Bandbreite von mehr als 1 GHz erforderlich macht. Da Aufklärungsradar mehrere Betriebsmodi besitzt, arbeitet dies System stets mit elektronisch schwenkbaren passiven oder zunehmend auch aktiven Array-Antennen mit Längen von 1 – 4 m in Azimut. Auf Bewegungskompensation und Echtzeitfähigkeit wird großer Wert gelegt; d.h. die Systeme erzeugen hoch aufgelöste Abbildungen an Bord und übermitteln sie den auswertenden Stellen am Boden. Die dazu erforderliche Rechenkapazität erfordert, sowohl beim Einbauvolumen, als auch bei der Primärenergie, den größten Teil der an Bord verfügbaren Ressourcen. Siehe auch SOSTAR-X.

Eine andere Klasse stellen Mini-SARs für den Einsatz an Bord von Marschflugkörpern (Drohnen) dar. Hier ist kleinstmöglichstes Bauvolumen bei hoher Auflösung (< 1 m) und mäßiger Streifenbreite (1 – 3 km) gefragt. Inzwischen kann auch bei diesen Anwendungen die erforderliche Prozessorkapazität an Bord installiert werden, so dass nur noch schon aufgearbeitete End-Ergebnisse per Telemetrie zum Boden übertragen werden müssen. Bei hohen Trägergeschwindigkeiten sind die erforderlichen Maßnahmen zur Bewegungskompensation gering, so dass der Prozessor an Bord durch diese Unter-Aufgabe nur verhältnismäßig wenig belastet ist.

Zivil wird das SAR praktisch ausschließlich zu Kartierungszwecken, fast stets in der Form des interferometrischen SAR an Bord von Turboprop-Maschinen aus eingesetzt. Deren geometrische Auflösung liegt üblicherweise im Bereich 0,5 – 2 m.

Satelliten-SAR

Anfänglich als reine Forschungsprojekte realisiert, tritt das Satelliten-SAR derzeitig in die Phase zunehmender militärischer und ziviler Nutzung ein. Militärisch wird die Aufklärung eines jeden Punktes auf der Erde innerhalb gegebener Zeiten mit Auflösungen im Bereich unter 1 m verlangt. Dazu sind mehrere Satelliten mit gleicher Ausrüstung und abgestimmten Flugbahnen erforderlich. Um die Kosten im Rahmen zu halten, sind Abstriche bei der Ausstattung unumgänglich. So ist die anfangs vor Jahren noch geforderte aktive Array-Antenne bei praktischen Systemen (z.B. SAR-Lupe) längst einer einfachen Reflektorantenne gewichen.

Auf ziviler Seite werden die forschungsorientierten SAR-Systeme der Vergangenheit allmählich durch kommerzielle Angebote zur Abbildung kundenspezifischer Areale abgelöst. Auch hier führt der Zwang zur Kostensenkung zur Bevorzugung möglichst einfacher Systeme.

SAR-Bild des indischen Ozeans.

Das Foto rechts zeigt ein SAR-Bildbeispiel. Die kleinen weißen Punkte sind Ölstationen, die schwarzen Flächen dünne Ölschichten. Die langperiodischen Wasserwellen oben sind sog. innere Wellen, die kleinen Wellen mit Wellenlängen um 100 m, siehe unterer Pfeil, sind durch Wind erzeugte Oberflächenwellen. Die Detailauflösung des 25 x 34 km² großen Areals ist besser als 100 m.

Von den Raumsonden Pioneer-Venus und Magellan wurde nach dem SAR-Verfahren der Planet Venus kartiert. Die Raumsonde Cassini-Huygens kartierte nach dem SAR-Verfahren den Saturnmond Titan.

Weitere Informationen über bereits realisierte oder in der Entstehung begriffene Satelliten-SAR-Systeme können den hier angeführten Seiten entnommen werden:

In Erdumlaufbahnen

• European Remote Sensing Satellite
• Envisat
• Shuttle Radar Topography Mission
• RADARSAT
• RADARSAT-2
• TerraSAR-X
• TanDEM-X
• SAR-Lupe
• COSMO-Skymed
• Active Electronically Scanned Array
• Lacrosse (Satellit)
• YaoGan WeiXing-1

Um andere Himmelskörper

• Magellan
• Pioneer-Venus
• Cassini-Huygens

Weblinks

• Sandia SAR
• Manuskripte und Präsentationen zum Thema SAR
• SAR in den Medien: Artikel "Stille Wächter über uns" in der Neuen Zürcher Zeitung (NZZ)

Literaturhinweise

Eine sehr anschauliche Darstellung zum Thema findet man bei:

• Hovanessian, Shahan A.: Introduction to Synthetic Array and Imaging Radar; Artech House, Dedham, MA; 1980
• Stimson, George W.: Introduction to Airborne Radar; Hughes Aircraft Comp., El Seghundo, CA; 1983

In Einzelkapiteln weitreichender Zusammenstellungen von Radaranwendungen und -technologien wird das SAR-Prinzip in den Büchern des Radar-"Papstes" Skolnik abgehandelt:

• Skolnik, Merrill, I.: Introduction to Radar Systems; McGraw-Hill Kogakusha Ltd., Tokyo; 1980; ISBN 0-070-66572-9
• Skolnik, Merrill, I.: Radar Handbook (2nd Ed.); McGraw-Hill, New York; 1990

Mehr auf der Theorie der Signalverarbeitung basierende Abhandlungen findet man bei:

• Barton, David K.: Radars Vol. 3, Pulse Compression; Artech House, Dedham, MA; 1975
• Wehner, Donald R.: High Resolution Radar; Artech House, Norwood, MA; 1987; ISBN 0-890-06194-7