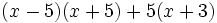- Termumformung
-
Dieser Artikel erläutert die Bedeutung des Begriffs Term in der Mathematik; Ein Artikel zum gleichnamigen Begriff aus der Linguistik findet sich unter Terminus. - 1
- 2(ab)3 + c
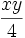
- 889 / (Hier fehlt der Divisor)
- [2x + 7) (Unpassende Klammern)
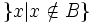(Verkehrte Klammer)- ausrechnen (dazu rechnet man erst die „inneren“ Funktionen aus und dann die äußeren),
- nach bestimmten Rechenregeln umformen,
- miteinander vergleichen (falls Relationen für die passenden Typen definiert sind)
- ineinander einsetzen (oft wird ein Term anstelle einer Variable eines anderen Terms eingesetzt).
- Jede Variable ist ein Term.
- Jedes Konstantensymbol ist ein Term.
- Ist t ein Term, so ist (t) ein Term.
- Sind
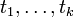Terme und f ist ein k-stelliges Funktionssymbol, so ist 
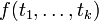ein Term. - Manche Funktionen (beispielsweise die Potenzfunktion, Multiplikation mit Variablen) werden statt durch ein eigenes Funktionssymbol durch Positionierung der Terme zueinander dargestellt.
- Bei verschachtelten Klammersetzungen werden manchmal auch [] und {} eingesetzt, um die Zusammengehörigkeit der Klammern deutlicher zu machen.
- x und y sind Terme (als Variablen),
- 4 ist ein Term (als Konstante),
- xy ist ein Term (eigentlich „multipliziere(x,y)“),
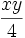- ist ein Term (Divisionssymbol ist der Bruchstrich)
- Rechnen mit Termen in der Schule
- Termumformungen mit didaktischen Hinweisen, Landesbildungsserver Baden-Württemberg
In der Mathematik bezeichnet Term einen sinnvollen Ausdruck, der Zahlen, Variablen, Symbole für mathematische Verknüpfungen und Klammern enthalten kann. Terme sind sozusagen die grammatisch korrekten Wörter oder Wortgruppen in der Sprache der Mathematik.
Terme stehen immer für mathematische Objekte wie Zahlen, Funktionen oder Mengen.
Inhaltsverzeichnis |
Beispiele
Beispiele für Terme:
Keine Terme sind:
Umgangssprachliche Erklärung
Der Begriff „Term“ wird umgangssprachlich für alles verwendet, das eine Bedeutung trägt: „Den Term [Ausdruck] versteh ich nicht.“ Im engeren Sinn gemeint sind mathematische Gebilde, die man prinzipiell ausrechnen kann (zumindest, wenn man den Variablen Werte zugewiesen hat), z. B. Zahlen, einfache und zusammengesetzte Funktionen (siehe die Beispiele oben), mit oder ohne Variablen.
Terme kann man
Eine spezielle Form der Einsetzung ist die Substitution, bei der ein Term mit Variablen durch einen anderen Term mit Variablen (meist eine einzelne Variable) ersetzt wird.
Formale Definition
Welche Ausdrücke Terme sind, ist genau festgelegt, sobald ein Zeichenvorrat aus Variablen, Konstanten und Funktionen festgelegt ist. Dabei gilt folgende formale Definition aus der mathematischen Logik (als rekursive Definition):
Anmerkungen:
Beispiel: 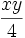ist ein Term, denn
Variablen in Termen
Treten in einem Term Variablen auf, wie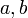 
oder 
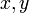in obigen Beispielen, so ist zusätzlich anzugeben, aus welcher Grundmenge diese Variablen zu wählen sind. Durch das Einsetzen von Elementen der Grundmenge erhält der Term einen konkreten Wert.
Zu beachten ist, dass der Term nicht unbedingt für alle Elemente der Grundmenge definiert sein muss; so ist beispielsweise für eine Funktion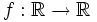 
und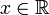 
der Term 
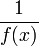nur für jene 
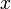definiert, für die 
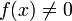gilt; jene Teilmenge der Grundmenge eines Termes, für die der Term wohldefiniert ist, wird als Definitionsmenge des Termes bezeichnet.
Anwendungen
Terme mit Variablen werden beispielsweise in Rechenvorschriften oder Formeln verwendet. So lautet eine Faustformel zum Ausrechnen des Anhalteweges (Bremsweg plus Reaktionsweg) eines Autos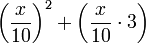 
, wobei in diesem Term x die Geschwindigkeit des Autos in km pro Stunde bedeutet. Wenn ein Auto zum Beispiel 160 km/h fährt, liefert die Formel 
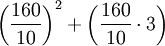einen Anhalteweg von 304m.
Terme können auch zur Definition der Zuordnungsvorschrift einer Funktion verwendet werden; das Beispiel des Anhalteweges definiert etwa die Funktion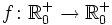 
, 
.
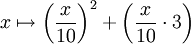Wie gesagt sind Terme selbst weder wahr noch falsch; es sind Symbole für Zahlen oder andere mathematische Objekte. Sie können aber zu mathematischen Aussagen wie Gleichungen und Ungleichungen zusammengefügt werden; solche Aussagen sind dann nach Einsetzen aller Variablen entweder wahr oder falsch.
Algebraische Umformungen
Lange, komplizierte Terme können oft vereinfacht werden, indem man auf sie Rechenregeln anwendet, die den Wert des Terms unverändert lassen, beispielsweise das Kommutativgesetz, Assoziativgesetz oder Distributivgesetz:
: 
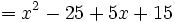: Gleichartige Ausdrücke zusammenfassen
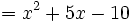
Solche algebraischen Umformungen sind von Äquivalenzumformungen für Gleichungen oder Ungleichungen zu unterscheiden. Algebraische Umformungen lassen den Wert eines Termes unverändert, Äquivalenzumformung ändern hingegen die Werte der beteiligten Terme, müssen aber den Wahrheitswert der Aussage unverändert lassen.
Daher sollten Terme, die durch Umformungen ineinander überführt werden können, als „gleich“ und nicht als „äquivalent“ bezeichnet werden.
Abgrenzungen
Term und Ausdruck
Der Begriff Term ist mit dem Begriff Ausdruck in formalen Sprachen verwandt. Während aber ein Ausdruck in einer formalen Sprache formal definiert ist, ist Term ein eher unscharf definierter Begriff. Da die Symbolik der Mathematik nicht fix definiert, sondern beliebig erweiterbar ist, ist auch Term ein erweiterbarer Begriff.
Durch Einführung zusätzlicher Definitionen kann eine vorher sinnlose Symbolkette eine Bedeutung bekommen; so kann beispielsweise je nach Zusammenhang die Symbolkette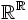 
sinnlos sein oder auch ein sinnvoller Term für die Menge aller Funktion von 
nach sein.
Term und Aussageform
Eine Aussageform ist wie ein Term eine formale Zeichenkette; ihr Aufbau ist gemäß einer Logik definiert, z. B. der Prädikatenlogik. In der Prädikatenlogik erster Stufe sind insbesondere folgende Ausdrücke Aussageformen:
Sind t1,t2 Terme, so ist t1 = t2 eine Aussageform.
Sind t1,...tk Terme und ist R ein k-stelliges Relationssymbol, so ist Rt1...tk eine Aussageform.
Eine Aussageform enthält wie ein Term möglicherweise Variablen, allerdings wird ihr nach Belegung der freien Variablen kein Wert der Grundmenge, sondern ein logischer Wahrheitswert (wahr oder falsch) zugeordnet.
Eine logische Aussage ist eine Aussageform ohne freie Variablen. Sie entsteht aus einer Aussageform durch Belegung oder durch Quantifikation der freien Variablen.
Weblinks
Wikimedia Foundation.
