Topozentrisches horizontales Koordinatensystem

Astronomische Koordinatensysteme sind Koordinatensysteme der Astrometrie, in denen die Stellung eines astronomischen Objekts beschrieben werden kann.

Alle gebräuchlichen Koordinatensysteme bestehen aus sphärischen Polarkoordinaten, das heißt sie definieren eine Achse, die die Pole markiert, und eine Nullrichtung in der Bezugsebene des Koordinatensystems. Sphärische Polarkoordinaten bestehen aus zwei Winkelkoordinaten, der Länge (Winkelabstand von der Nullrichtung in der Bezugsebene) und der Breite (Höhenwinkel über der Bezugsebene), sowie einer Radiuskoordinate für den Abstand. Die Radiuskoordinate wird im Allgemeinen weggelassen, da sie für das Finden der Objekte am Himmel keine Rolle spielt.

Absolute Koordinatensysteme

Es gibt 3 gebräuchliche absolute Koordinatensysteme, die die Position am Sternhimmel angeben: die Äquatorialkoordinaten, Ekliptikalkoordinaten und galaktische Koordinaten genannt werden.

Darstellung von Deklination, Rektaszension, Ekliptik und Frühlingspunkt

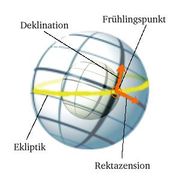
• Bei den Äquatorialkoordinaten ist die Polachse die Rotationsachse der Erde, die Bezugsebene mit der Äquatorebene der Erde identisch. Als Koordinatennullpunkt dient der Frühlingspunkt. Die Länge in diesen Koordinaten wird Rektaszension genannt und meist in Stunden, Minuten und Sekunden angegeben, eine Koordinatenstunde entspricht 15 Grad. Die Breite wird Deklination genannt und in Grad angegeben.
• Ekliptikalkoordinaten benutzen die Ekliptik als Bezugsebene und ebenfalls den Frühlingspunkt als Nullpunkt. Die Koordinaten heißen ekliptikale Länge und Breite und werden in Grad angegeben. Dieses Koordinatensystem wird oft für Positionsangaben von Körpern in unserem Sonnensystem benutzt.
• Bei galaktischen Koordinaten ist die Ebene der Milchstraßenscheibe die Bezugsebene, der Nullpunkt ist durch das galaktische Zentrum festgelegt. Zum Beispiel für Untersuchungen zur Struktur der Milchstraße sind diese Koordinaten sehr praktisch. Da sich die Sonne nicht genau in der Scheibenebene der Milchstraße befindet, sondern einige Lichtjahre davon entfernt, wurde die exakte Ausrichtung willkürlich, aber in guter Näherung an die tatsächliche Scheibenebene definiert. Die Ebene der Milchstraße ist ca. 57° gegen die Ebene der Ekliptik geneigt.

Bei Koordinatensystemen, die sich auf den Frühlingspunkt beziehen, muss zusätzlich ein Zeitpunkt angegeben werden, für den die Koordinaten gelten, weil sich der Frühlingspunkt durch die Präzession gegen den Sternenhimmel verschiebt. Es muss also der Zeitpunkt des Äquinoktiums angegeben werden den, für den die Koordinaten katalogisiert sind (Äquinoktium der Koordinaten). Die Epoche der Koordinaten ist dagegen der Zeitpunkt einer echten Beobachtung. Der Unterschied zwischen Epoche und Äquinoktium ergibt sich aus der Eigenbewegung der Himmelsobjekte.

Beispiel: Die Position eines Sterns wird am 1. Januar 1950 gemessen. Diese Koordinaten haben Epoche und Äquinoktium 1950.0. Unter Berücksichtigung der Präzession werden die Koordinaten auf das Jahr 2000 umgerechnet. Diese Koordinaten haben Äquinoktium 2000.0, aber Epoche 1950.0. Erst bei vollständiger Berücksichtigung der Eigenbewegung kann man die Position für die Epoche 2000.0 angeben, also die Koordinaten, an denen der Stern tatsächlich am Neujahrstag 2000 stünde.

Standardepoche und Äquinoktium für astronomische Kataloge ist derzeit 2000.0. Kataloge mit Koordinaten für 1950.0 sind aber immer noch gebräuchlich.

Relative Koordinatensysteme

Daneben gibt es noch zwei relative Koordinatensysteme, die nur für einen jeweils festen Ort auf der Erdoberfläche, beispielsweise ein Observatorium, gelten. Die absoluten Himmelskoordinaten eines Objekts werden für die Beobachtung in diese relativen Koordinaten umgerechnet (transformiert). Welches benutzt wird, hängt von der jeweiligen Teleskopmontierung ab.

• Stundenwinkel': Für äquatoriale Montierungen wird die Deklination einfach übernommen, als Längenkoordinate wird der Stundenwinkel ausgerechnet, der die Differenz der lokalen Sternzeit zur Rektaszension ist. Dies ist auch der historische Grund für die Angabe der Längenkoordinate in einer Einheit der Zeit (siehe oben). Es ist somit ein System mit gleicher Ausrichtung wie bei den Äquatorialkoordinaten, der Nullpunkt ist aber der örtliche Südmeridian, auf dem die Himmelsobjekte kulminieren, also ihren höchsten Punkt über dem Horizont erreichen.
• Azimutale Koordinaten' (horizontale Koordinaten): Teleskope mit einer azimutalen Montierung benutzen den Horizont als Bezugsebene, die Zenit-Nadir-Achse als Polachse. Die Koordinaten sind damit die Höhe oder Altitude, und der Azimut, für den als Nullpunkt meist die Südrichtung gewählt wird. Die auch Alt-az abgekürzten Koordinaten werden mit Hilfe einer Koordinatentransformation aus den absoluten Himmelskoordinaten umgerechnet. Siehe hierzu auch Nautisches Dreieck.

Heliozentrisch, geozentrisch, topozentrisch oder baryzentrisch

Alle Koordinatensystem können im Prinzip heliozentrisch (auf den Sonnenmittelpunkt bezogen), geozentrisch (auf den Erdmittelpunkt bezogen, topozentrisch (auf den Standpunkt des Beobachters bezogen) oder baryzentrisch (auf den Schwerpunkt eines Systems bezogen) gerechnet werden. In der faktischen Anwendung wird nur eine Auswahl davon verwendet:

• heliozentrische eklipikale Koordinaten und baryzentrische ekliptikale Koordinaten für Berechnungen im Sonnensystem
• geozentrische ekliptikale Koordinaten und geozentrische äquatoriale Koordinaten für Berechnungen in Bezug auf die Erde
• topozentrische ekliptikale Koordinaten, topozentrische äquatoriale Koordinaten und topozentrische azimutale (horizontale) Koordinaten für Anblicksprobleme der beobachtenden Astronomie wie auch die Bahnberechnungen für Erdsatelliten
• Die galaktischen Koordinaten, die im Fundamentalsystem angegeben sind, werden meist über baryzentrische ekliptikale Koordinaten auf den jeweiligen Bezugspunkt transformiert.
• Daneben wird in der Himmelsmechanik etwa im Erde-Mond-System auch auf den Erde-Mond-Schwerpunkt bezogen baryzentrisch, oder beim Jupiter und seinen Monden auf den Jupitermittelpunkt bezogen jovizentrisch gerechnet, und für viele weitere spezielle Problemstellungen andere passende Bezugspunkte gewählt.

Weblinks

Caligo: Kostenloses Programm zum Umrechnen horizontaler in äquatoriale Koordinaten und umgekehrt