- Typ-I-C*-Algebra
-
Postliminale C*-Algebren sind eine in der Mathematik betrachtete Klasse von C*-Algebren. Alternative Bezeichnungen, die weiter unten motiviert werden, sind GCR-Algebra oder Typ-I-C*-Algebra. Es handelt sich um eine Verallgemeinerung der Klasse der liminalen C*-Algebren.
Inhaltsverzeichnis
Definition
Eine C*-Algebra A heißt postliminal, wenn für jedes echte, abgeschlossene, zweiseitige Ideal
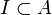 die Quotientenalgebra A / I ein von {0} verschiedenes liminales Ideal enthält.
die Quotientenalgebra A / I ein von {0} verschiedenes liminales Ideal enthält.Damit ist der Begriff der postliminalen C*-Algebra auf den der liminalen C*-Algebra zurückgeführt und stellt offenbar eine Verallgemeinerung dar. Das wird auch durch die erste der folgenden Charakterisierungen deutlich.
Charakterisierungen
Bilder irreduzibler Darstellungen
Ist π eine irreduzible Darstellung der C*-Algebra A auf dem Hilbertraum H, so enthält A / ker(π) nach Definition ein von {0} verschiedenes liminales Ideal. Man kann zeigen, dass durch
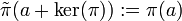 eine irreduzible Darstellung
eine irreduzible Darstellung 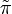 dieses Ideals definiert wird. Da I liminal ist, fällt das Bild
dieses Ideals definiert wird. Da I liminal ist, fällt das Bild 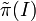 mit der Algebra K(H) der kompakten Operatoren zusammen und daraus folgt
mit der Algebra K(H) der kompakten Operatoren zusammen und daraus folgt 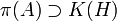 . Das Bild einer jeden irreduziblen Darstellung umfasst also die kompakten Operatoren und davon gilt sogar die Umkehrung:
. Das Bild einer jeden irreduziblen Darstellung umfasst also die kompakten Operatoren und davon gilt sogar die Umkehrung:- Eine C*-Algebra A ist genau dann postliminal, wenn
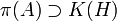 für jede irreduzible Darstellung
für jede irreduzible Darstellung 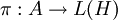 von A.
von A.
Für liminale C*-Algebren hat man eine fast gleich lautende Charakterisierung, die Inklusion ist lediglich durch eine Gleichheit ersetzt (siehe Artikel liminale C*-Algebra). Da man liminale C*-Algebren wegen dieser Beziehung zu den kompakten Operatoren auch CCR-Algebren nennt (CCR=completely continuous representations), heißen postliminale C*-Algebren aus demselben Grunde auch GCR-Algebren (GCR = generalized completely continuous representations).
Kompositionsreihen
Eine Kompositionsreihe einer C*-Algebra A ist eine Familie
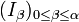 von abgeschlossenen, zweiseitigen Idealen
von abgeschlossenen, zweiseitigen Idealen 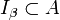 , wobei
, wobei- α ist eine Ordinalzahl (β durchläuft also alle Ordinalzahlen bis α einschließlich.)
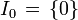 und
und 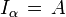 .
.- Für
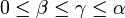 gilt
gilt 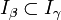
- Ist
![\gamma \in [0,\alpha]](/pictures/dewiki/100/d2b64361f56792f5951ebe4e2a001935.png) eine Limeszahl, so ist Iγ der Abschluss von
eine Limeszahl, so ist Iγ der Abschluss von 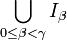 .
.
Mit dieser Begriffsbildung kann man folgende Charakterisierung beweisen:
- Eine C*-Algebra A ist genau dann postliminal, wenn es eine Kompositionsreihe
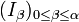 von A gibt, so dass alle Quotienten Iβ + 1 / Iβ liminal sind.
von A gibt, so dass alle Quotienten Iβ + 1 / Iβ liminal sind.
Im Falle separabler C*-Algebren kann man hier den Begriff der Ordinalzahl umgehen, denn wenn die Ideale der Kompositionsreihe alle verschieden sind (was keine weitere Einschränkung darstellt), so ist α maximal
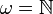 und man kann die Kompositionsreihe mit natürlichen Zahlen indizieren.
und man kann die Kompositionsreihe mit natürlichen Zahlen indizieren.Typ I
Eine Darstellung
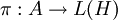 einer C*-Algebra A heißt vom Typ I, falls die vom Bild π(A) erzeugte von-Neumann-Algebra vom Typ I ist, das heißt wenn der Bikommutant
einer C*-Algebra A heißt vom Typ I, falls die vom Bild π(A) erzeugte von-Neumann-Algebra vom Typ I ist, das heißt wenn der Bikommutant 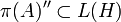 eine Typ-I-von-Neumann-Algebra ist.
eine Typ-I-von-Neumann-Algebra ist.- Eine C*-Algebra A ist genau dann postliminal, wenn jede Darstellung vom Typ I ist.
Daher nennt man postliminale C*-Algebren auch Typ-I-C*-Algebren. Diese Bezeichnung kann aber zur Verwirrung Anlass geben, denn eine Typ-I-von-Neumann-Algebra, die ja auch eine C*-Algebra ist, ist im Allgemeinen keine Typ-I-C*-Algebra, wie das Beispiel A = L(H) mit unendlich-dimensionalem Hilbertraum H zeigt.
Spektrum
Ist [π] eine Äquivalenzklasse irreduzibler Darstellungen von A, also ein Element des Spektrums
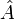 , so hängt das Ideal ker(π) nur von der Äquivalenzklasse [π] und nicht von der konkreten Darstellung π ab. Da die Kerne irreduzibler Darstellungen definitionsgemäß die primitiven Ideale sind, ist die Kernbildung eine Abbildung
, so hängt das Ideal ker(π) nur von der Äquivalenzklasse [π] und nicht von der konkreten Darstellung π ab. Da die Kerne irreduzibler Darstellungen definitionsgemäß die primitiven Ideale sind, ist die Kernbildung eine Abbildung 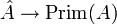 vom Spektrum in den Raum der primitiven Ideale. Diese ist nach Konstruktion surjektiv, im Allgemeinen aber nicht injektiv.
vom Spektrum in den Raum der primitiven Ideale. Diese ist nach Konstruktion surjektiv, im Allgemeinen aber nicht injektiv.- Ist A eine postliminale C*-Algebra, so ist die Kernabbildung
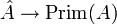 injektiv. Ist A separabel, so gilt hiervon die Umkehrung.
injektiv. Ist A separabel, so gilt hiervon die Umkehrung.
Es ist offen, ob die genannte Umkehrung auch im Falle nicht-separabler C*-Algebren gilt.
Beispiele
- Liminale C*-Algebren sind postliminal.
- Es sei T die vom Shiftoperator
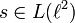 erzeugte C*-Algebra, die sogenannte Toeplitz-Algebra (nach Otto Toeplitz). Da 1 − sns * n die Orthogonalprojektion auf den von den Basisvektoren
erzeugte C*-Algebra, die sogenannte Toeplitz-Algebra (nach Otto Toeplitz). Da 1 − sns * n die Orthogonalprojektion auf den von den Basisvektoren 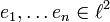 erzeugten Unterraum und damit ein kompakter Operator ist, kann man zeigen, dass
erzeugten Unterraum und damit ein kompakter Operator ist, kann man zeigen, dass 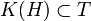 . Weiter gilt, dass
. Weiter gilt, dass 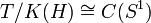 , wobei
, wobei 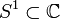 die Kreislinie ist, denn T / K(H) wird von der Restklasse s + K(H) erzeugt, und diese hat die Kreislinie als Spektrum. Man hat sogar eine exakte Sequenz
die Kreislinie ist, denn T / K(H) wird von der Restklasse s + K(H) erzeugt, und diese hat die Kreislinie als Spektrum. Man hat sogar eine exakte Sequenz
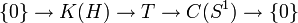
.
- Jedenfalls ist durch I0: = {0},I1: = K(H),I2: = T eine Kompositionsreihe von T gegeben, und die Quotienten
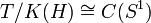 und
und 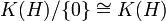 sind liminal. Daher ist T postliminal, aber nicht liminal, denn
sind liminal. Daher ist T postliminal, aber nicht liminal, denn  ist eine irreduzible Darstellung, die den nicht-kompakten Operator s im Bild enthält.
ist eine irreduzible Darstellung, die den nicht-kompakten Operator s im Bild enthält.
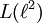 ist ein Beispiel für eine C*-Algebra, die nicht postliminal ist. Die Calkin-Algebra ist ein weiteres Beispiel einer nicht-postliminalen C*-Algebra.
ist ein Beispiel für eine C*-Algebra, die nicht postliminal ist. Die Calkin-Algebra ist ein weiteres Beispiel einer nicht-postliminalen C*-Algebra.
Eigenschaften
- Eine Unter-C*-Algebra einer postliminalen C*-Algebra ist wieder postliminal.
- Ist
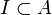 ein abgeschlossenes, zweiseitiges Ideal in der postliminalen C*-Algebra A, so ist auch A / I postliminal.
ein abgeschlossenes, zweiseitiges Ideal in der postliminalen C*-Algebra A, so ist auch A / I postliminal. - Ist
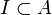 ein abgeschlossenes, zweiseitiges Ideal in der C*-Algebra A und sind I und A / I postliminal, so ist auch A postliminal.
ein abgeschlossenes, zweiseitiges Ideal in der C*-Algebra A und sind I und A / I postliminal, so ist auch A postliminal. - Postliminale C*-Algebren sind nuklear.
- Ist A postliminal, so besitzt A eine Kompositionsreihe
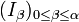 , so dass alle Quotienten Iβ + 1 / Iβ C*-Algebren mit stetiger Spur sind. Das verschärft die oben mittels Kompositionsreihen gegebene Charakterisierung.
, so dass alle Quotienten Iβ + 1 / Iβ C*-Algebren mit stetiger Spur sind. Das verschärft die oben mittels Kompositionsreihen gegebene Charakterisierung. - Eine postliminale C*-Algebra A ist genau dann liminal, wenn jeder Punkt in
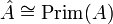 abgeschlossen bzgl. der Zariski-Topologie ist, das heißt wenn das Spektrum
abgeschlossen bzgl. der Zariski-Topologie ist, das heißt wenn das Spektrum 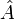 ein T1-Raum ist.
ein T1-Raum ist.
Quellen
- W. Arveson: Invitation to C*-algebras, ISBN 0387901760
- J. Dixmier: Les C*-algèbres et leurs représentations, Gauthier-Villars, 1969
- Eine C*-Algebra A ist genau dann postliminal, wenn
Wikimedia Foundation.
