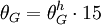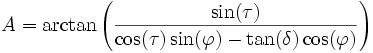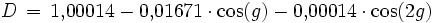Stand der Sonne

Der Sonnenstand ist die Position der Sonne am Himmel. Er hängt vom Beobachtungsort und von der Tageszeit und der Jahreszeit ab. Folglich dient der Sonnenstand zur Darstellung der mit einer Sonnenuhr messbaren Tages- und Jahreszeit. Der Sonnenstand bestimmt unter anderem auch den Einfallswinkel und die Intensität des Sonnenlichts.

Der zeitliche Verlauf des Sonnenstands ist die Sonnenbahn, das ist die scheinbare Umlaufbahn der Sonne auf der Himmelskugel. Dargestellt wird die Sonnenbahn in Verlauf eines Tages und eines Sonnenjahres mit dem Sonnenstandsdiagramm.

Mitternacht am 24. Juni 2005 in Helsinki; Restlicht der Sonne

Astronomie

Insbesondere spricht man von hohem oder von niedrigem Sonnenstand und von seiner Veränderung im Laufe der Jahreszeiten. Ihren höchsten Stand erreicht die Sonne jeweils zu Mittag (genauer: um 12 Uhr wahre Ortszeit) im Süden (für einen Beobachter nördlich des nördlichen Wendekreises) bzw. im Norden (für einen Beobachter südlich des südlichen Wendekreises). Diese sogenannte „Mittagshöhe“ hängt von der geografischen Breite und dem Datum ab; auf 50° Breite variiert sie zwischen 16,5° zur Wintersonnenwende und 63,5° zur Sommersonnenwende (siehe Schiefe der Ekliptik).

Umwelt

Vom Sonnenstand und seiner Veränderlichkeit hängen eine Reihe wichtiger Größen ab, vor allem

• die Intensität der Sonnenstrahlung. Aus ihr ergeben sich weiters
• die Klimazone (zusammen mit den Feuchtigkeits- und Bewölkungsverhältnissen) und die Arten der Vegetation
• der Bedarf an Heizung beziehungsweise an Kühlung
• die Entstehung lokaler Winde (siehe beispielsweise Aufwind) und die Wolkenbildung, aber auch
• regionale Winde (wie Monsun) und viele Meeresströmungen
• die Entstehung von Siedlungsstrukturen, insbesondere im Gebirge.

Kultur

Die Messung des Sonnenstandes durch Sonnenuhren ermöglicht den Menschen seit Jahrtausenden die Bestimmung der Tageszeit und die Einteilung des Jahres durch Kalenderrechnung. In der frühen Antike war sie die erste Methode der Erdmessung und wurde mit dem Aufkommen spezieller Messinstrumente zu einer wichtigen Methode der Navigation.

Der tägliche „Weg der Sonne über den Himmel“ spielt bei verschiedenen Mythologien eine große Rolle, etwa bei Helios' „Sonnenwagen“ der griechischen Antike und in der Deutung von Sonnenauf- und Untergang. Bewohner der Nordhemisphäre sind oft, wenn sie die Südhemisphäre bereisen, erstaunt über die „Umkehrung“ der täglichen scheinbaren Sonnenbewegung „nach links“.

Sonnenstandsdiagramm

Sonnenstandsdiagramm für Wiesbaden (50° Nord, 8,25° Ost):
am 15. Oktober, 13:52 Uhr steht die Sonne ungefähr 27° über Horizont im Südwesten, siehe roter Punkt

auf eine Kugel projiziertes Sonnenstandsdiagramm: Tagbögen der Sonne sind Kreise, wie auf der Himmelskugel

Ein Sonnenstandsdiagramm ist die Umkehr dessen, was eine Sonnenuhr leistet: Der Sonnenstand gibt Datum und Tageszeit an.

Aus einem Sonnenstandsdiagramm eines Ortes lassen sich bei bekanntem Datum und bekannter Uhrzeit Richtung und Höhe der Sonne ablesen. So kann man die Besonnung eines bestimmten Ortes im Laufe eines Tages und eines Jahres bestimmen.

Im Laufe eines Tages wandert die Sonne scheinbar entlang eines „Tagbogens“ von Ost über Süd nach West, um dort unterzugehen. Dieser Tagbogen ist in unten stehenden Diagrammen für die jeweils Monatsersten eingezeichnet: im ersten Halbjahr als durchgezogene Linien, ab Juli als gestrichelte Linien. Der Sonnenstand ist für jede volle Tagesstunde ebenfalls eingezeichnet: Die Stundenlinien haben die Form eines Analemmas, da die Zeitgleichung berücksichtigt ist. Die in den Diagrammen aufgrund der gewählten Projektion „gewellt“ erscheinenden Tagbögen sind in Wirklichkeit Kreise auf der Himmelskugel, wie die Projektion auf eine Kugel zeigt (Abbildung rechts).

An weiter südlich gelegenen Orten (kleinere geographische Breite φ) erreicht die Sonne größere Mittagshöhen. Wie weit die Sonne um 12 Uhr MEZ von der Südrichtung entfernt ist, hängt von der Lage des Ortes in der Mitteleuropäischen Zeitzone ab: für Orte, die westlich vom Referenzmeridian 15° Ost liegen (zum Beispiel Wiesbaden, etwa 8,25° Ost) hat die Sonne die Südrichtung zu diesem Zeitpunkt noch nicht erreicht, für östlich von 15° Ost gelegene Orte (zum Beispiel Wien, etwa 16,35° Ost) hat sie sie bereits überschritten.

Ein Sonnenstandsdiagramm kann auch helfen, die Ausrichtung einer Wand zu bestimmen: Liegt diese im Streiflicht, so kann man mit der Uhrzeit und dem Datum aus dem Sonnenstandsdiagramm das Azimut ablesen.

Berechnung

Der Sonnenstand für einen gegebenen Zeitpunkt lässt sich nach gängigen Methoden mit beliebiger Genauigkeit berechnen (z.B. nach der Planetentheorie VSOP87). Für Anwendungen mit mäßigen Anforderungen genügt die im Folgenden beschriebene stark vereinfachte Methode, die einen günstigen Kompromiss zwischen Genauigkeit und Rechenaufwand darstellt.

Ekliptikalkoordinaten der Sonne

Der gewünschte Zeitpunkt ist zuerst in Weltzeit UT umzurechnen (UT = MEZ-1h = MESZ-2h). Als Zeitvariable n wird die Anzahl der Tage seit dem Standardäquinoktium J2000.0 (1. Januar 2000, 12 Uhr TT ≈ 12 Uhr UT) verwendet, gegebenenfalls inklusive Tagesbruchteil. Ist JD die Julianische Tageszahl des gewünschten Zeitpunkts, so gilt

$n \, = \, JD \, - \, 2451545{,}0$.

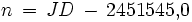Zunächst ist die Position der Sonne auf der Ekliptik zu bestimmen. Sieht man vorerst von den durch die Bahnelliptizität verursachten Geschwindigkeitsschwankungen ab und setzt eine mittlere Geschwindigkeit der Sonne an (360° in ca. 365,2422 Tagen), so erhält man die mittlere ekliptikale Länge L der Sonne (in dieser Formel ist auch der Einfluss der Aberration bereits enthalten):

$L \, = \, 280{,}460^\circ + 0{,}9856474^\circ \cdot n$.

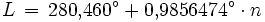Um den Einfluss der Bahnelliptizität nachträglich zu berücksichtigen und die ekliptikale Länge Λ zu erhalten, ist hierzu als Korrektur die so genannte Mittelpunktsgleichung zu addieren. Diese Korrektur hängt vom Winkel zwischen Sonne und Perihel ab, der so genannten Anomalie. Die Mittelpunktsgleichung erwartet als Eingabewert die (fiktive) gleichförmig anwachsende mittlere Anomalie g. Diese wächst um 360° in einem anomalistischen Jahr zu ca. 365,2596 Tagen:

$g \, = \, 357{,}528^\circ + 0{,}9856003^\circ \cdot n$.

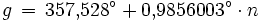Die Mittelpunktsgleichung ist eine periodische Funktion der mittleren Anomalie und kann daher in eine Fourierreihe zerlegt werden. Bei kleinen Bahnexzentrizitäten kann die Reihe nach wenigen Termen abgebrochen werden. Berücksichtigt man nur in der (numerischen) Exzentrizität e lineare und quadratische Terme, so lautet die Mittelpunktsgleichung

$\Lambda - L \, = \, \left( 2 e \sin(g) + \frac{5}{4} e^2 \sin(2g) \right) \, \cdot \, \frac{180^\circ}{\pi}$,

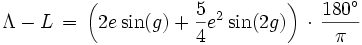und für den Fall der Sonnenbahn mit 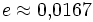$e \approx 0{,}0167$ ergibt sich daraus für die ekliptikale Länge Λ der Sonne:

$\Lambda \, = \, L + 1{,}915^\circ \cdot \sin(g) + 0{,}020^\circ \cdot \sin(2g)$.

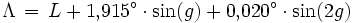L und g sollten vorher durch Addition oder Subtraktion geeigneter Vielfacher von 360° in den Bereich zwischen 0° und 360° gebracht werden. Alternativ zur Benutzung der Mittelpunktsgleichung kann die ekliptikale Länge auch mit Hilfe der Keplergleichung aus der mittleren Länge berechnet werden, was jedoch ein iteratives Lösungsverfahren erfordert.

Äquatorialkoordinaten

Für die so berechnete, entlang der Ekliptik gezählte, ekliptikale Länge Λ muss nun die zugehörige entlang des Himmelsäquators gezählte Rektaszension α bestimmt werden. Mit der Schiefe der Ekliptik $\varepsilon$

$\varepsilon \, = \, 23{,}439^\circ - 0{,}0000004 \cdot n$

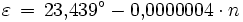
ergibt sich die Rektaszension α als

$\alpha \, = \, \arctan\left( \frac{\cos(\varepsilon) \sin(\Lambda)}{\cos(\Lambda)} \right)$.

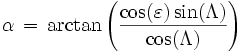Falls der Nenner im Argument des Arcustangens einen Wert kleiner Null hat, sind 180° zum Ergebnis zu addieren, um den Winkel in den richtigen Quadranten zu bringen (α muss im gleichen Quadranten liegen wie Λ). Alternativ zur hier benutzten exakten Formel kann für die Berechnung von α auch eine Reihenentwicklung benutzt werden; siehe die Berechnungsmethode für die Zeitgleichung.

Die senkrecht zum Himmelsäquator gezählte Deklination δ ergibt sich als

$\delta \, = \, \arcsin(\sin(\varepsilon) \sin(\Lambda))$.

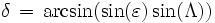Fehlerabschätzung

Der Fehler der vereinfachten Sonnenstandsformel des Astronomical Almanac bleibt im Zeitraum von 1950 bis 2050 fast immer unter 0,01°.

Wie die nebenstehende Grafik zeigt, erreichen die so berechneten Koordinaten der Sonne für den Zeitraum von 1950 bis 2050 eine Genauigkeit von etwa 0,01°. Der auffälligste Restfehler der ekliptikalen Länge hat eine regelmäßige Periode von 18,6 Jahren und eine Amplitude von 0,0047°; es handelt sich um die in der Rechnung nicht berücksichtigte Nutation in Länge. Zu den Rändern der Grafik hin wächst die Schwankungsbreite der Restfehler deutlich an. Dies wird durch die nicht berücksichtigte Änderung der Exzentrizität der Erdbahn verursacht, die bei der Berechnung der Koeffizienten der Mittelpunktsgleichung als konstant mit dem Wert für das Jahr 2000 angesetzt worden war. Dieser Fehler hat das anomalistische Jahr als Periode; seine Amplitude wächst in 100 Jahren um 0,0048°. Des Weiteren sind jene Bahnstörungen vernachlässigt, die sich unmittelbar auf die ekliptikale Länge auswirken; vor allem die Störungen durch Jupiter (Terme mit Amplituden 0,0019°, 0,0014°, ...), Mond (Terme mit Amplituden 0,0017°, ...), Mars (Terme mit Amplituden 0,0014°, 0,0011°, ...) und Venus (Terme mit Amplituden 0,0014°, 0,0011°, ...). Dass die ekliptikale Breite stillschweigend konstant auf Null gesetzt wurde erzeugt keinen merklichen Fehler. Die berechneten Koordinaten sowie die Vergleichsdaten gelten für einen geozentrischen Beobachter; für einen realen Beobachter auf der Erdoberfläche kann die beobachtete Sonnenposition um bis zu 0,0024° (die Sonnenparallaxe) davon abweichen.

Werden genauere Daten benötigt, können diese mit aufwendigeren Verfahren berechnet oder von einem der zahlreichen Ephemeridenserver im Web bezogen werden (siehe Weblinks).

Azimut, Höhe

Das Ergebnis ist bei Bedarf noch auf die Koordinaten Azimut A (d.h. Himmelsrichtung) und Höhenwinkel h umzurechnen. Dazu bestimme man die Julianische Tageszahl JD₀ für 0^h UT des betrachteten Datums, berechne zunächst

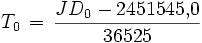$T_0 \, = \, \frac{JD_0 - 2451545{,}0}{36525}$ in julianischen Jahrhunderten (1 julianisches Jahr = 365,25 Tage) ab J2000.0

und damit die mittlere Sternzeit θ_G in Greenwich für den gesuchten Zeitpunkt T (Weltzeit UT, in Stunden):

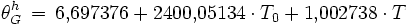$\theta^h_G \, = \, 6{,}697376 + 2400{,}05134 \cdot T_0 + 1{,}002738 \cdot T$ in Stunden und Bruchteilen einer Stunde (sprich 17,75 für 17:45 Uhr).

Der erste Term ist die Sternzeit von Greenwich zum Zeitpunkt J2000.0, der zweite die Drift des Frühlingspunktes seit J2000.0

Die Sternzeit ist der Stundenwinkel des Frühlingspunktes, ausgedrückt im Zeitmaß (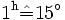$1^\mathrm{h} \hat= 15^\circ$). Ganzzahlige Vielfache von 24^h können gegebenenfalls vom Ergebnis abgezogen werden. Multiplikation mit dem Umrechnungsfaktor 15 °/h liefert den Greenwich-Stundenwinkel des Frühlingspunkts im Gradmaß:

$\theta_G = \theta^h_G \cdot 15$

Für einen Ort auf der geographischen Länge λ (nach Osten positiv gezählt) ist der Stundenwinkel des Frühlingspunkts

$\theta \, = \, \theta_G + \lambda$,

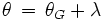und Subtraktion der Rektaszension der Sonne α liefert den Stundenwinkel τ der Sonne für jenen Ort:

$\tau \, = \, \theta - \alpha$.

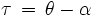Azimut A und Höhenwinkel h ergeben sich für einen Ort auf der geographischen Breite $\varphi$ aus

$A = \arctan\left( \frac{\sin(\tau)}{\cos(\tau) \sin(\varphi) - \tan(\delta) \cos(\varphi)} \right)$

sowie

$h \, = \, \arcsin(\cos(\delta) \cos(\tau) \cos(\varphi) + \sin(\delta) \sin(\varphi))$.

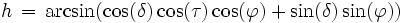Falls der Nenner im Argument des Arcustangens einen Wert kleiner Null hat, sind 180° zum Ergebnis zu addieren, um den Winkel in den richtigen Quadranten zu bringen. Der nach der genannten Formel berechnete Azimut wird von Süden aus gezählt. Soll er von Norden aus gezählt werden, sind 180° zum Ergebnis zu addieren.

Korrektur wegen Refraktion

Schließlich ist bei Bedarf noch die Refraktion (Lichtbrechung in der Atmosphäre) zu berücksichtigen, welche die Sonnenscheibe etwas höher erscheinen lässt als sie tatsächlich steht. Die mittlere Refraktion (in Bogenminuten) für ein Objekt, das sich auf der Höhe h (in Grad) befindet, lässt sich näherungsweise berechnen durch

$R \, = \, \frac{1{,}02}{\tan\left( h + \frac{10{,}3}{h + 5{,}11} \right)}$.

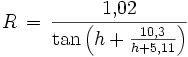Die refraktionsbehaftete Höhe in Grad ist dann

$h_R \, = \, h + R/60$.

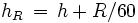Es ist zu beachten, dass die Refraktion vom detaillierten Zustand der Atmosphäre abhängt. Die angegebene Formel nimmt einen Luftdruck von 1010 mbar und eine Temperatur von 10° C an. Hiervon abweichende Bedingungen können durch geeignete Korrekturen berücksichtigt werden, aber auch dann beschreibt die Formel nur eine mittlere Refraktion, während die tatsächlichen Werte besonders in unmittelbarer Horizontnähe je nach aktueller Temperaturschichtung unter Umständen merklich von diesem Mittel abweichen können.

Sonstige Sonnendaten

Die Entfernung D der Sonne von der Erde beträgt zum betrachteten Zeitpunkt

$D \, = \, 1{,}00014 - 0{,}01671 \cdot \cos(g) - 0{,}00014 \cdot \cos(2g)$ Astronomische Einheiten,

und ihr scheinbarer Radius

$0{,}2666^\circ / D$.

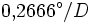Die Differenz L − α, multipliziert mit 4, liefert die Zeitgleichung in Minuten.

Beispiel

Es ist der Sonnenstand für den 6. August 2006 um 8 Uhr MESZ (T = 6 Uhr UT) in München ($\varphi$ = 48,1° N, λ = 11,6° O) zu bestimmen. Es ergeben sich

$JD \, = 2453953{,}75$	$n \, = 2408{,}75 \, \mathrm{d}$	$L \, = 2654{,}638^\circ \, \stackrel{\wedge}= \, 134{,}638^\circ$
$g \, = 2731{,}593^\circ \, \stackrel{\wedge}= \, 211{,}593^\circ$	$\Lambda \, = 133{,}653^\circ$	$\varepsilon \, = 23{,}438^\circ$
$\alpha \, = -43{,}881^\circ + 180^\circ = 136{,}119^\circ$	$\delta \, = 16{,}726^\circ$	$JD_0 \, = 2453953{,}5$
$T_0 \, = 0{,}06594113621$	$\theta^h_G \, = 170{,}9759^\mathrm{h} \, \stackrel{\wedge}= \, 2{,}9759^\mathrm{h}$	$\theta \, = 56{,}239^\circ$
$A \, = 85{,}938^\circ + 180^\circ = 265{,}938^\circ \, \stackrel{\wedge}= \, -94{,}062^\circ$	$h \, = 19{,}062^\circ$	$h_R \, = 19{,}110^\circ$

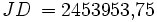
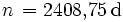
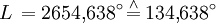
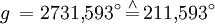
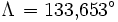
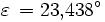
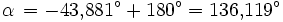
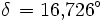
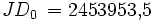
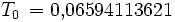
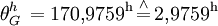
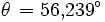
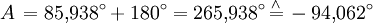
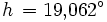
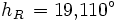
Ein Astronomieprogramm (SkyMap 2.2) liefert zum Vergleich 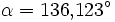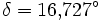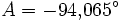$\alpha = 136{,}123^\circ$, $\delta = 16{,}727^\circ$, $A = -94{,}065^\circ$ und $h_R = 19{,}106^\circ$.

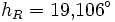Die Rechnungen sind mit einer ausreichenden Stellenzahl zu führen (z.B. doppelter Genauigkeit, bei achtstelligen Taschenrechnern ist Vorsicht geboten); insbesondere für T₀ müssen ausreichend viele Stellen berücksichtigt werden. Es ist zu beachten, dass manche Rechenprogramme und Programmiersprachen Winkelangaben im Bogenmaß und nicht in Grad erwarten; die Winkel sind dann entsprechend umzurechnen.

Siehe auch

• Sonnenaufgang/Sonnenuntergang sowie Aufgang (Astronomie) zu deren Berechnung
• Kulmination/Meridiandurchgang, Zeitgleichung - zum Problem von Mittag und Südrichtung
• Ost-West-Vertikal, Digression - weitere Hauptaspekte
• Ephemeridenrechnung, Sonnentafel - tabellierte Werte der Hauptaspekte
• Breitengrad/Längengrad, Ortszeit - zum Problem lokaler Zeitangaben
• Sonnenenergie, Sonnenscheindauer, Schattenlänge, Sonnenuhr

Weblinks

• http://cgi.stadtklima-stuttgart.de/mirror/sonne.exe aktueller Sonnenstand für beliebige Standorte
• http://www.wetter-herrenberg.de/interaktives/Strahlung/sonnenstand.htm#elev instruktive Grafik zum Tagesgang der Sonne am 21. Juni und 21. Dezember.
• http://sonnenstand.stephan-brumme.com weltweiter Sonnenstand
• http://www.calsky.com/cs.cgi/Sun? Ephemeridenserver
• http://ssd.jpl.nasa.gov/?horizons Ephemeridenserver für höchste Ansprüche (englisch)
• http://www.westfilm.ch/sonnenstand Tool zur visuellen Darstellung des Sonnenstandes mit Google Earth

Sonnenstandsdiagramme verschiedener Städte

Sonnenstandsdiagramm für Hamburg, φ=53,5°	Sonnenstandsdiagramm für Berlin, φ=52,5°	Sonnenstandsdiagramm für Köln, φ=51°
Sonnenstandsdiagramm für München, φ=48,2°	Sonnenstandsdiagramm für Wien, φ=48,2°	Sonnenstandsdiagramm für Bern, φ=47°

Quellen

Berechnung von α und δ: (AstAlm 2006), S. C24
Berechnung von A und h: (Meeus 2000), Kap. 12, 13. Die hier wiedergegebene Sternzeitformel wurde wegen der geringeren Genauigkeitsansprüche gegenüber der originalen Formel vereinfacht. Der Fehler bleibt im Zeitraum von 1950 bis 2050 kleiner als 0,0001°, wächst außerhalb dieser Grenzen wegen Vernachlässigung eines quadratischen Terms aber quadratisch an.
Refraktion: (Meeus 2000), Kap. 16
Fehlerdiskussion der vereinfachten Sonnenstandsberechnung: Nutation (Meeus 2000) Kap. 22; Störungen (vFPu 1979)
Auf- und Untergang: Definition, 16'+34': (Meeus 2000), Kap. 15

• (AstAlm 2006) The Astronomical Almanac For The Year 2006, The Stationery Office, London 2004, ISBN 0-11-887333-4
• (Meeus 2000) Jean Meeus: Astronomical Algorithms, Willmann-Bell, Richmond 2000 (2nd ed., 2nd printing), ISBN 0-943396-61-1
• (vFPu 1979) Van Flandern, T.C., Pulkkinen, K.F.: Low-Precision Formulae for Planetary Positions, ApJ Supp. 41, 391-411 (1979) (PDF)