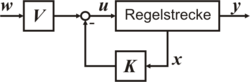
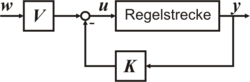
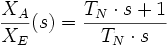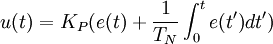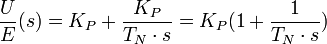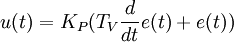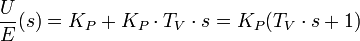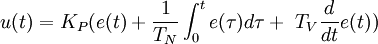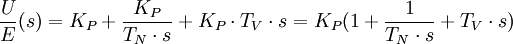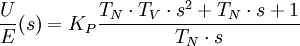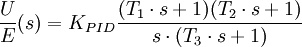Zustandsrückführung

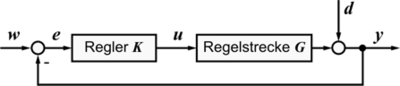Blockschaltbild eines einfachen Standardregelkreises, bestehend aus der Regelstrecke 'G', dem Regler 'K' und einer negativen Rückkopplung der Regelgröße 'y' (auch: Istwert) auf den Regler. Die Regeldifferenz 'e' wird aus der Differenz zwischen der Führungsgröße 'w' (auch: Sollwert) und der Regelgröße errechnet. Der vom Regler ermittelte Stellwert 'u' wirkt auf die Strecke und damit wiederum auf die Regelgröße ein. Die Störgröße d bewirkt eine Veränderung der Regelgröße, die nicht gewünscht ist und kompensiert werden muss.

Regler beeinflussen selbsttätig in einem meist technischen Prozess eine oder mehrere physikalische Größen auf ein vorgegebenes Niveau unter Reduzierung von Störeinflüssen. Ihre Behandlung ist Kern der Regelungstechnik.

Dazu vergleichen Regler innerhalb eines Regelkreises laufend das Signal des Sollwertes mit dem gemessenen und zurückgeführten Istwert der Regelgröße und ermitteln aus dem Unterschied der beiden Größen – der Regelabweichung (Regeldifferenz) – eine Stellgröße, welche die Regelstrecke so beeinflusst, dass die Regelabweichung spätestens im eingeschwungenem Zustand zu einem Minimum wird.

Weil die einzelnen Regelkreisglieder beim Signaldurchlauf ein Zeitverhalten haben, muss der Regler den Wert der Regelabweichung verstärken und gleichzeitig das Zeitverhalten der Strecke so kompensieren, dass die Regelgröße den Sollwert in gewünschter Weise – von aperiodisch bis gedämpft schwingend – erreicht. Falsch eingestellte Regler machen den Regelkreis zu langsam, führen zu einer großen Regelabweichung oder zu ungedämpften Schwingungen der Regelgröße und unter Umständen zur Zerstörung der Regelstrecke. Neben dem Einschwingverhalten der Regelgröße auf den Sollwert interessiert:

• Regelabweichung bei statischen und dynamischen Eingangsgrößen,
• Regelabweichung bei statischen und dynamischen Störgrößen.

Das Verhalten der Regelkreisglieder wird durch Differentialgleichungen beschrieben. Bei linearen Systemen ist es vorteilhaft, die Regelkreisglieder nicht im Zeitbereich, sondern im Frequenzbereich als Übertragungsfunktion zu betrachten.

Der Frequenzgang ist ein Spezialfall der Übertragungsfunktion. Er kennzeichnet das Verhalten eines Systems mit erzwungener Dauerschwingung und der imaginären Frequenz p=jω. Beide Begriffe unterscheiden sich nur durch die Entstehungsweise. Der entscheidende Vorteil der Umwandlung der Funktionen vom Zeitbereich zum Frequenzbereich ist die algebraische Behandlung der Übertragungsfunktionen.

Sämtliche Daten für die Kriterien der Stabilität, wie Pole, Nullstellen, Verstärkung und Zeitkonstanten, lassen sich aus den Übertragungsfunktionen der Regelkreisglieder ableiten.

Hier wird auf dynamische Reglerstrukturen und deren gerätetechnische Realisierung eingegangen. Der Entwurf (Parametrierung) des Reglers ist Gegenstand eigener Artikel, auf die an geeigneter Stelle verwiesen wird.

Einführung und Übersicht

Der Einsatz von Reglern ist so vielfältig und unterschiedlich, wie es Regelaufgaben aus allen Bereichen des Haushaltes, der Industrie, der Luft- und Raumfahrt, Forschung usw. gibt.

Die Auslegung und Funktion des Reglers ist neben wirtschaftlichen Aspekten ausschließlich von der Art der Regelstrecke und dem geforderten zeitlichen Verlauf der Regelgröße – dem Führungs- und Störverhalten – abhängig.

Man unterscheidet zwei Arten von Reglern, stetige Regler und unstetige Regler. Unstetige Regler sind Regler, deren Stellwert nach unstetigen mathematischen Gesetzen gebildet werden. Zu den unstetigen Reglern gehören die 2-Punkt-, Mehrpunkt- und Fuzzy-Regler.

Mit dem Problem, für jede Strecke einen optimalen Regler zu finden, beschäftigt sich die optimale Regelung.

Geschichte der Regler

Historisch dokumentierte Regeleinrichtungen sind seit dem 18. Jahrhundert bekannt. Dazu gehört z. B. ein Wasserstandsregler über Schwimmer und besonders erwähnenswert ist der 1788 erfundene Zentrifugalregulator von James Watt zur Drehzahlregelung von Dampfmaschinen.

Aus der früheren Regelungstechnik des 20. Jahrhundert ist ein Fallbeispiel eines mechanischen Programmreglers zu nennen.

Stetige Regler

Stetige Regler mit analogem oder digitalem Verhalten können für lineare Regelstrecken verwendet werden.

Digitale Regler haben den Vorteil einer universellen Anpassung an die unterschiedlichsten Regelaufgaben, jedoch verlangsamen sie den Regelprozess durch die Abtastzeit der Regelgröße und Rechenzeit im Einsatz bei schnellen Regelstrecken.
Für einschleifige lineare Regelsysteme kommen je nach Verhalten der Regelstrecke meistens die klassischen analogen P-, PI-,PD- und PID-Regler zur Anwendung.
Viele nicht stabile Regelstrecken, die z. B. durch positive Rückkopplungseffekte (Mitkopplung) entstehen können, sind ebenfalls mit diesen Reglern beherrschbar.

Für komplexere Regeleinrichtungen mit nichtlinearen Regelstrecken oder mehrere miteinander verknüpfte Regelgrößen und Stellgrößen sind besonders angepasste Regler – meist digitale Regler – erforderlich. Hierbei kommen vermaschte Regelungen, Mehrgrößenregelungen, Regelungen im Zustandsraum, modellbasierte Regelungen usw. zum Einsatz.

Klassische lineare Regler

Die Übertragungsfunktion eines Systems entsteht z. B. durch Austausch der zeitabhängigen Terme einer Differentialgleichung mit den Laplace-Transformierten. Voraussetzung ist, dass die Anfangsbedingung des Systems Null ist.

Lautet beispielsweise die Differentialgleichung eines PID-Reglers:

$u(t)=K_P\left(e(t)+\frac1{T_N}\int e(t)dt+T_V\frac d{dt}e(t)\right)$

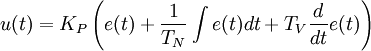
Die Terme e(t), deren Ableitung und Integral werden durch die Laplace-Transformierten E(s) ersetzt:

$U(s)=K_P(E(s)+\frac{E(s)}{T_N\cdot s}+T_V\cdot s\cdot E(s))$

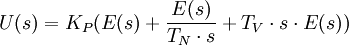
Die Übertragungsfunktion ist definiert als das Verhältnis von Ausgang zu Eingang einer Funktion:

$\frac U{E}(s)=K_P(1+\frac 1{T_N\cdot s}+T_V\cdot s)=K_P \frac {T_N \cdot T_V \cdot s^2+T_N \cdot s+1}{T_N \cdot s}$

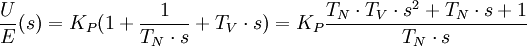
In der linearen Regelungstechnik ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (stabilen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf folgende drei Grundformen geschrieben bzw. zurückgeführt werden können. Sie haben eine völlig unterschiedliche Bedeutung, ob sie im Zähler oder im Nenner einer Übertragungsfunktion stehen:

Typ Übertragungsfunktion	Bedeutung im Zähler	Bedeutung im Nenner
G1(s)=T*s	Differenzierer, D-Glied	Integrator, I-Glied
G2(s)=T*s+1	PD-Glied	Verzögerung, T1-Glied
G3(s)=T²*s²+2*D*T*s+1	PD-Glied 2. Ordnung	2 T1-Glieder oder Schwingungsglied für 0<D<1

Dabei bedeuten:

T = Zeitkonstante, s = komplexe Frequenz = Laplace-Operator, D= Dämpfungsgrad,

Die Zeitkonstanten im Frequenzbereich entsprechen einer dimensionslosen Zahl.

Bei sogenannten nichtregulären (instabilen) Systemen lauten die Übertragungsfunktionen:

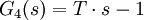$G_4(s)=T\cdot s-1$ und $G_5(s)=T^2\cdot s^2-2DT\cdot s+1$

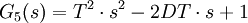
Liegen Zähler- oder Nennerpolynome der Übertragungsfunktion vor, müssen erst die Nullstellen je nach Grad der Polynome gegebenenfalls mit aufwendigen Rechenverfahren ermittelt werden, um die Polynome in faktorielle Grundglieder zu zerlegen.

Regelsysteme können definiert werden als:

• Reihenschaltung: 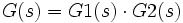$G(s)=G1(s) \cdot G2(s)$. Es gilt das Superpositionsprinzip. Die Systeme in Produktdarstellung können in der Reihenfolge beliebig verschoben werden, Systemausgänge werden nicht durch nachfolgende Eingänge belastet.
• Parallelschaltung: $G(s)=G1(s)\pm G2(s)$,
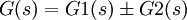• Gegen- und Mitkopplung: $G(s)= G1/(1 \pm G1\cdot G2)$

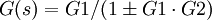
Die linearen Standard-Regler wie:

• P-Regler (P-Glied) mit proportionalem Verhalten,
• I-Regler (I-Glied) mit integralem Verhalten,
• PI-Regler (1 I-Glied, 1 PD-Glied) mit proportionalem und integralem Verhalten,
• PD-Regler (PD-Glied) mit proportionalem und differentialem Verhalten,
• PID-Regler (1 I-Glied, 2 PD-Glieder) mit proportionalem, integralem und differentialem Verhalten, lassen sich bereits mit den ersten beiden der genannten Terme der Grundformen der Übertragungsfunktionen in faktorieller Darstellung beschreiben.

Beispielsweise lautet die Produktdarstellung eines PI-Reglers:

• $\frac {X_A}{X_E}(s)=\frac {T_N\cdot s+1}{T_N \cdot s}$

Es handelt sich also bei einem PI-Regler um einen Regler mit einem P-Glied und einem I-Glied mit der Verstärkung K_PI = 1 / T_n

Diese Produktdarstellung ist auch für den Entwurf des Reglers sehr bedeutsam, weil sich die Terme der Übertragungsfunktionen algebraisch behandeln lassen. So können bei Kenntnis der Übertragungsfunktionen der Strecke durch den Regler Anteile der Strecke mit gleichen Zeitkonstanten kompensiert werden, d. h. Nullstellen des Reglers kompensieren Polstellen der Strecke um die Ordnung der Regelstrecke zu reduzieren. Dies ist sowohl algebraisch als auch durch Betrachtung im Bodediagramm verständlich. Die Auslegung des Reglers vereinfacht sich auf diese Weise.

Ein weiterer Vorteil der Produktdarstellung der Übertragungsfunktion ist die Darstellung des Frequenzgangs im Bodediagramm. Die Pole und Nullstellen können direkt abgelesen werden.

P-Regler (P-Anteil)

Sprungantwort P-Anteil mit K=2

Der P-Regler besteht ausschließlich aus einem proportionalen Anteil der Verstärkung K_p. Mit seinem Ausgangssignal u ist er proportional dem Eingangssignal e.

Das Übergangsverhalten lautet: $u(t) = K_p\cdot e(t)$.

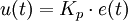Die Übertragungsfunktion lautet:

$\frac UE(s)=K_P$

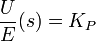
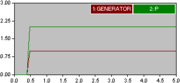
Das Diagramm zeigt das Ergebnis einer Sprungantwort. Der P-Regler hat eine gewählte Verstärkung von K_p = 2.

Eigenschaften des P-Reglers:

• Wegen des fehlenden Zeitverhaltens reagiert der P-Regler unmittelbar, jedoch ist sein Einsatz sehr begrenzt, weil die Verstärkung je nach Verhalten der Regelstrecke stark reduziert werden muss.
• Der Regelfehler einer Sprungantwort nach dem Einschwingen der Regelgröße als „bleibenden Regelabweichung“ beträgt 100 % / Kp, wenn kein I-Glied in der Strecke enthalten ist.
• Bei einer Regelstrecke mit einem T1-Glied (Verzögerungsglied 1. Ordnung) kann die Verstärkung theoretisch unendlich hoch gewählt werden, weil ein Regelkreis mit einer solchen Regelstrecke nicht instabil werden kann. Dies kann anhand des Stabilitätskriterium von Nyquist nachgeprüft werden. Die bleibende Regelabweichung ist praktisch vernachlässigbar. Das Einschwingen der Regelgröße ist aperiodisch.
• Bei einer Regelstrecke mit zwei T1-Gliedern und zwei dominanten Zeitkonstanten sind die Grenzen dieses Reglers erreicht. Zum Beispiel ergibt die Sprungantwort bei Kp = 10 eine bleibende Regelabweichung von 10 %, eine erste Überschwingung von 35 % bei einem Dämpfungsgrad D = 0,18. Mit steigender Verstärkung wird die Regelabweichung kleiner, die Überschwingung größer und die Dämpfung schlechter. Diese Daten gelten für zwei gleiche Zeitkonstanten und sind unabhängig von deren Größe.

I-Regler (I-Anteil)

Sprungantwort I-Anteil

Ein I-Regler (integrierender Regler, I-Glied) wirkt durch zeitliche Integration der Regelabweichung e auf die Stellgröße mit der Gewichtung durch die Nachstellzeit T_N.

Die Differentialgleichung lautet:

$u(t)=\frac1{T_N}\int_0^t e(t')\cdot dt'$

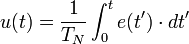
Die Übertragungsfunktion lautet:

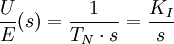$\frac U{E}{(s)}=\frac 1{T_N\cdot s} = \frac {K_I}{s}$ Verstärkung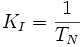 $K_I=\frac 1{T_N}$

Die Zeitkonstante T_N ist im Frequenzbereich dimensionslos.

Eine konstante Regeldifferenz e(t) führt von einem Anfangswert des Ausgangs u1(t) zum linearen Anstieg des Ausgangs u2(t) bis zu seiner Begrenzung. Die Nachstellzeit T_N bestimmt den Gradienten des Anstiegs.

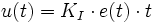$u(t) = K_I \cdot e(t) \cdot t$ für e(t) = konstant

Die Nachstellzeit z. B. T_N = 2s bedeutet, dass zur Zeit t=0 der Ausgangswert u nach 2 s die Größe des konstanten Eingangswertes e erreicht hat.

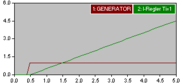
Das Diagramm zeigt das Ergebnis der Sprungantwort des I-Gliedes. Die Zeitkonstante beträgt T_i = 1s. Der Eingangssprung hat die Größe e = 1.

Zusammenfassung der Eigenschaften des I-Reglers:

• Der I-Regler ist durch seine (theoretisch) unendliche Verstärkung ein genauer, aber langsamer Regler. Er hinterlässt keine bleibende Regelabweichung. Weil er eine zusätzliche Nullstelle mit einem Phasenwinkel von −90° im aufgeschnittenen Regelkreis einfügt, kann nur eine schwache Verstärkung KI bzw. große Zeitkonstante Tn eingestellt werden.
• Für eine Regelstrecke mit zwei T1-Gliedern kann bei zwei dominanten Zeitkonstanten bereits volle Instabilität bei geringer Verstärkung KI entstehen. Für diese Art Regelstrecken ist der I-Regler kein geeigneter Regler.
• Bei einer Regelstrecke mit I-Glied im Regelkreis ohne zusätzliche Verzögerungen gilt für alle Werte der Kreisverstärkung 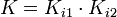$K = K_{i1} \cdot K_{i2}$ Instabililität mit konstanter Amplitude. Die Schwingfrequenz ist eine Funktion von K (für K>0).
• Der I-Regler ist die erste Wahl für eine Regelstrecke mit dominanter Totzeit Tt oder Totzeit ohne weitere T1-Glieder. Eventuell kann ein PI-Regler eine minimale Verbesserung erzielen. Optimale Einstellung bei vernachlässigbaren Verzögerungen:

K_I = 0,5 / T_t für eine Überschwingung von 4 %, die Regelgröße erreicht den Sollwert nach 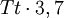$Tt \cdot 3,7$, D=0,5. Diese Einstellungen gelten für alle Tt-Werte

• Großsignalverhalten: Beim I-Regler tritt bei Überschreiten der Stellgrößenbegrenzung (der Stellgrößen-Ausgang des Reglers überschreitet die physikalischen Grenzen des Stellglieds) ein Wind-up-Effekt auf, d. h. der I-Regler nimmt einen Wert oberhalb der Möglichkeiten des Stellgliedes ein und verursacht beim Rücklauf ungewollte Verzögerungen. Dem tritt man mit der Begrenzung des I-Anteils auf die Stellgrößen-Grenzen entgegen (Anti-Windup).
• Grenzzyklen: Bei nichtlinearem Streckenverhalten, insbesondere trockener Reibung, kommt es zu sogenannten Grenzzyklen. Hierbei kann das Stellglied den Sollzustand zunächst nicht exakt herstellen, da die Stellgröße nicht zur Überwindung einer Haftreibung ausreicht. Der sich aufbauende I-Anteil sorgt für die Überwindung der Haftreibung, es findet aber unmittelbar der Übergang zur kleineren Gleitreibung statt. Bis sich der I-Anteil auf einen Wert unterhalb der Gleitreibung eingestellt hat, ist der Sollwert überschritten. Der gleiche Vorgang wiederholt sich dann mit umgekehrten Vorzeichen bis zur Ausgangsposition. Es kommt zu einem andauernden Hin-und-her-rucken. Zur Vermeidung wird meist einfach ein Regelfehler mit einem Betrag unterhalb einer geeigneten Grenze zu null gesetzt.

D-Glied (D-Anteil)

Sprungantwort D-Anteil

Das D-Glied ist ein Differenzierer, der nur in Verbindung zu Reglern mit P- und/oder I-Verhalten als Regler eingesetzt wird. Er reagiert nicht auf die Regelabweichung, sondern nur auf deren Änderungsgeschwindigkeit.

Differentialgleichung: $u(t)={T_V}\frac {d}{dt}e(t)$

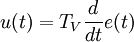
Übertragungsfunktion: $\frac U{E}{(s)=T_V\cdot s}$

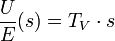
Tv = Vorhaltzeit, Tv = KD, KD = Differenzierbeiwert
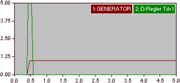
"Vorhaltzeit" (Begriff laut DIN 19226 Teil 2) wird umgangssprachlich fälschlicherweise oft als "Vorhaltezeit" bezeichnet.

Die Sprungantwort des (idealen) D-Gliedes, wie im zugehörigen Diagramm gezeigt, ist eine Stoßfunktion mit theoretisch unendlicher Größe. Der Eingangssprung ist als Testsignal nicht geeignet.

Ein brauchbares Testsignal für das D-Glied ist die Anstiegsfunktion:

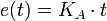$e(t)=K_A\cdot t$ mit der Anstiegskonstante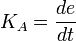 $K_A=\frac {de}{dt}$

Nach der Laplace-Transformation wird $E(s) =\frac {K_A}{s^2}$

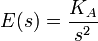
Die Anstiegsfunktion E(s) wird in der Übertragungsfunktion des D-Gliedes eingesetzt. Damit wird die Ausgangsgröße des D-Gliedes:

$U(s)=T_V\cdot K_A\frac s{s^2}= {T_V\cdot K_A}\frac 1{s}$

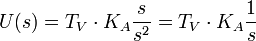
und nach der Rücktransformation wird die Ausgangsgröße:

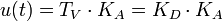$u(t)=T_V\cdot K_A=K_D \cdot K_A$, Tv=KD

Daraus ist ersichtlich, dass eine Anstiegsfunktion ein konstantes Ausgangssignal am D-Glied hervorruft. Die Größe des Ausgangssignals ist von dem Produkt Anstiegskonstante und Differenzierbeiwert abhängig.

Das bisher betrachtete Verhalten gilt für den idealen Differenzierer. Allgemein gilt ein System, dessen Übertragungsfunktion im Zähler eine höhere Ordnung als im Nenner aufweist, als technisch nicht realisierbar. Es ist nicht möglich, beliebig schnelle Eingangssignale wie z. B. beim Eingangssprung durch unvertretbar hohe Stellgrößenamplituden zu verwirklichen. Deshalb wird zu dem Differenzierer eine kleine Verzögerung (T1-Glied) zugefügt, deren Zeitkonstante T wesentlich kleiner sein muss als die Zeitkonstante Tv. Die Übertragungsfunktion des realen D-Gliedes lautet damit:

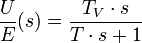$\frac U{E}(s)=\frac{T_V\cdot s}{T\cdot s+1}$ mit Tv>>T

Eine Sprungantwort des realen D-Gliedes verläuft mit begrenzter Größe des Stoßes asymptotisch nach Null.
Die Beachtung der realen Übertragungsfunktion gilt in erster Linie der Realisierung des Reglers in analoger Technik. Siehe PID-Regler!

Zusammenfassung der Eigenschaften des D-Gliedes:

• Es kann nur differenzieren, nicht regeln.
• Es wird vorzugsweise als Komponente in PD- und PID-Reglern eingesetzt.
• Es kann theoretisch als ideales D-Glied ein I-Glied einer Regelstrecke vollständig bei gleichen Zeitkonstanten kompensieren.
• Eine lineare Anstiegsfunktion am Eingang bewirkt eine konstante Ausgangsgröße, die proportional der Zeitkonstante Tv ist.
• Die Sprungantwort ist eine Stoßfunktion, die beim realen D-Glied eine endliche Größe aufweist und nach einer e-Funktion auf Null abklingt.

PI-Regler

Sprungantwort PI-Regler

Der PI-Regler (proportional–integral controller) besteht aus den Anteilen des P-Gliedes K_p und I-Gliedes. Er kann sowohl aus reiner Parallelstruktur oder aus einer gemischten Reihen- und Parallelstruktur definiert werden.

Bei der reinen Parallelstruktur ist es deshalb notwendig, dass das I-Glied mit der Verstärkung K_p multipliziert wird. Anschließend wird K_p dann als gemeinsamer Faktor vor den Klammerausdruck gesetzt.

Differentialgleichung:

• $u(t)=K_P(e(t)+\frac 1{T_N}\int_0^t{e(t')}dt')$

Übertragungsfunktion in der Summendarstellung

• $\frac U{E}{(s)}=K_P+\frac{K_P}{T_N\cdot s}=K_P(1+\frac 1{T_N\cdot s})$

Wird der Klammerausdruck der Gleichung auf einen gemeinsamen Nenner gebracht, entsteht die Produktdarstellung:

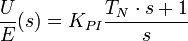• $\frac U{E}{(s)}=K_{PI}\frac{T_N\cdot s+1}{s}$ Kpi = Kp/Tn ist die Verstärkung des PI-Reglers

Aus dieser Produktdarstellung der Übertragungsfunktion ist ersichtlich, dass zwei Regelsysteme als Einzelsysteme zu einer Reihenschaltung geworden sind. Es handelt sich hierbei um ein PD-Glied und um ein I-Glied mit der Verstärkung K_pi, welche sich aus den Beiwerten K_p und T_N errechnen.
Signaltechnisch wirkt der PI-Regler gegenüber dem I-Regler nach einem Eingangssprung, dass dessen Wirkung um die Nachstellzeit Tn vorverlegt ist. Durch den I-Anteil wird die stationäre Genauigkeit gewährleistet, die Regelabweichung wird nach dem Einschwingen der Regelgröße zu Null, richtige Parametrierung vorausgesetzt.

Zusammenfassung der Eigenschaften des PI-Reglers:

• Er kann mit dem PD-Glied ein T1-Glied der Strecke kompensieren und damit die Regelstrecke vereinfachen.
• Durch das I-Glied wird im stationären Zustand die Regelabweichung zu Null. Nachteilig ist die Wirkung einer zusätzlichen Polstelle mit −90° Phasenwinkel in dem offenen Regelkreis. Deshalb ist der PI-Regler kein schneller Regler.
• Es gibt nur zwei Einstellparameter, K_pi und T_N
• Er kann optimal an einer Regelstrecke höherer Ordnung eingesetzt werden, von der nur die Sprungantwort bekannt ist. Durch Ermittlung der Ersatztotzeit T_U = Verzugszeit und der Ersatzverzögerungs-Zeitkonstante T_G = Ausgleichszeit kann das PD-Glied des Reglers die Zeitkonstante T_G kompensieren. Für die I-Regler-Einstellung der verbleibenden Regelstrecke mit Ersatztotzeit gelten die bekannten Einstellvorschriften.
• Er kann eine Regelstrecke mit zwei dominanten Zeitkonstanten von T1-Gliedern regeln, wenn die Kreisverstärkung reduziert wird und die längere Dauer des Einschwingens der Regelgröße auf den Sollwert akzeptiert wird. Dabei kann mit Kpi jeder gewünschte Dämpfungsgrad D eingestellt werden, von aperiodisch (D=1) bis schwach gedämpft schwingend (D gegen 0).

PD-Regler

Sprungantwort PD-Regler

Der PD-Regler (proportional–derivative controller) besteht aus der Kombination eines P-Gliedes Kp mit einem D-Glied. Die Übertragungsfunktion kann aus der Parallelstruktur definiert werden, wenn auch das D-Glied mit der P-Verstärkung Kp multipliziert wird. Kp wird dann als gemeinsamer Faktor vor den Klammerausdruck gesetzt.

Die Differentialgleichung lautet:

• $u(t)=K_P(T_V\frac d{dt}e(t)+e(t))$

Die Übertragungsfunktion lautet für den idealen Regler:

• $\frac U{E}{(s)}=K_P+K_P\cdot T_V\cdot s=K_P(T_V \cdot s+1)$

Wie beim D-Glied gilt auch hier für ein System, dessen Übertragungsfunktion im Zähler eine höher Ordnung als im Nenner aufweist, als technisch nicht realisierbar. Es ist nicht möglich, beliebig schnelle Eingangssignale wie z. B. beim Eingangssprung, unvertretbar hohe Stellgrößen-Amplituden zu verwirklichen. Deshalb wird zu dem Differenzierer eine kleine Verzögerung (T1-Glied) zugefügt, deren Zeitkonstante T wesentlich kleiner sein muss als die Zeitkonstante T_v.

Die Übertragungsfunktion des realen PD-Regler lautet damit:

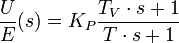• $\frac U{E}{(s)}=K_P\frac {T_V\cdot s+1}{T\cdot s+1}$ für T_v>>T

Die Beachtung der realen Übertragungsfunktion gilt in erster Linie der Realisierung des Reglers in analoger Technik. Es ist zu prüfen, ob die Verzögerung gegenüber anderen Verzögerungen im offenen Regelkreis vernachlässigt werden kann.
Für die Realisierung in digitaler Technik tritt das Problem der großen Stellgrößenamplituden nicht auf.

Die Sprungantwort ist wie beim D-Glied eine Stoßfunktion, die beim PD-Regler dem P-Anteil überlagert ist. Deshalb ist die Anstiegsfunktion für den PD-Regler das geeignete Testsignal.

Für die Anstiegsfunktion definiert sich die Vorhaltzeit T_v als die Zeit, bei der ein reiner P-Regler vor beginn der Anstiegsfunktion beginnen müsste, um auf den Wert zu kommen, den das D-Glied bewirkt.

Der PD-Regler ist ein sehr schneller Regler, denn er fügt im Gegensatz zum PI-Regler keinen zusätzlichen Pol in den offenen Regelkreis ein. Gegenüber dem P-Regler kann der PD-Regler ein T1-Glied kompensieren. Der Nachteil der bleibenden Regelabweichung begrenzt seine Verwendung.

Zusammenfassung der Eigenschaften des PD-Reglers:

• Er kann ein T1-Glied der Regelstrecke kompensieren und damit die Regelstrecke vereinfachen.
• Der ideale PD-Regler kann gegenüber dem P-Regler bei einer Regelstrecke mit zwei T1-Gliedern theoretisch mit unendlich hoher Verstärkung arbeiten. Die bleibende Regelabweichung ist praktisch vernachlässigbar. Das Einschwingen der Regelgröße ist aperiodisch.
• Der Regelfehler einer Sprungantwort nach dem Einschwingen der Regelgröße als bleibenden Regelabweichung beträgt 100 / Kp [%].

PID-Regler

Grundsätzliches Strukturbild eines PID-Reglers

Sprungantwort PID-Regler

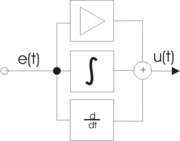
Der PID-Regler (proportional–integral–derivative controller) besteht aus den Anteilen des P-Gliedes Kp, des I-Gliedes und des D-Gliedes. Er kann sowohl aus reiner Parallelstruktur oder aus einer gemischten Reihen- und Parallelstruktur definiert werden.

In dem Strukturbild ist die Parallelschaltung dargestellt.

Bei der reinen Parallelstruktur ist es deshalb notwendig, dass das I-Glied und das D-Glied mit der Verstärkung Kp multipliziert wird. Anschließend wird Kp dann als gemeinsamer Faktor vor den Klammerausdruck gesetzt.

Differentialgleichung:

• $u(t)=K_P(e(t)+\frac 1{T_N}\int_0^t{e(\tau)}d\tau+\ T_V \frac d{dt}e(t))$

Übertragungsfunktion in Summendarstellung:

• $\frac U{E}{(s)}=K_P+\frac {K_P}{T_N\cdot s}+K_P\cdot T_V\cdot s=K_P(1+\frac 1{T_N\cdot s}+T_V\cdot s)$

Wird der Klammerausdruck der Gleichung auf einen gemeinsamen Nenner gebracht, entsteht die Produktdarstellung:

• $\frac U{E}{(s)}=K_P\frac{T_N\cdot T_V\cdot s^2+T_N\cdot s+1}{T_N\cdot s}$

Das Zählerpolynom kann durch die Bestimmung der Nullstellen aufgelöst werden. Damit lautet die ideale Übertragungsfunktion in Produktdarstellung:

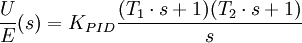• $\frac U{E}{(s)}=K_{PID}\frac{(T_1\cdot s+1)(T_2\cdot s+1)}{s}$ Mit der Reglerverstärkung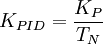 $K_{PID}=\frac {K_P}{T_N}$

Wie beim D-Glied und PD-Regler gilt auch hier ein System, dessen Übertragungsfunktion im Zähler eine höher Ordnung als im Nenner aufweist, als technisch nicht realisierbar.

Es ist nicht möglich, beliebig schnelle Eingangssignale wie z. B. beim Eingangssprung, durch unvertretbar hohe Stellgrößenamplituden zu verwirklichen.

Ist die Regelgröße mit einem nicht zu vernachlässigen Rauschanteil behaftet, muss ein kleiner Filter realisiert werden. Deshalb wird der Übertragungsfunktion eine kleine Verzögerung (T1-Glied) zugefügt, deren Zeitkonstante T (hier T3) wesentlich kleiner sein muss als die Zeitkonstanten T1 und T2.

Damit lautet die reale Übertragungsfunktion in Produktdarstellung:

• $\frac U{E}{(s)}=K_{PID}\frac{(T_1\cdot s+1)(T_2\cdot s+1)}{s\cdot (T_3\cdot s+1)}$

Die Zeitkonstante T3 wird auch als parasitäre Zeitkonstante bezeichnet. T3<<T1 und T2. Die durch Polynomauflösung entstandenen Zeitkonstanten T1 und T2 sind mit den ursprünglichen Zeitkonstanten Tn, Tv und der Verstärkung miteinander verknüpft.

Die Beachtung der realen Übertragungsfunktion gilt in erster Linie der Realisierung des Reglers in analoger Technik. Für die Realisierung des PID-Reglers in digitaler Technik, genügt die Anwendung der idealen Übertragungsfunktion, sofern das Messrauschen der Regelgröße – wie in den meisten Fällen – vernachlässigbar ist. Die Sprungantwort des D-Anteils als Stoßfunktion beim quasikontinuierlichen Differenzieren ist ohnehin durch die Abtastzeit und Rechenzeit begrenzt. Es können keine unzulässig hohen Stellgrößenänderungen auftreten.

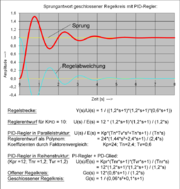
Anders als die klassische Darstellung der Übertragungsfunktion des PID-Reglers in Parallelstruktur und Produktdarstellung kann ein PID-Regler auch aus der Reihenschaltung eines PI-Reglers und eines PD-Gliedes zusammengesetzt werden. Die Übertragungsfunktionen unterscheiden sich äußerlich nicht, jedoch ist die Bedeutung der Koeffizienten unterschiedlich. Die Koeffizienten dieses zusammengesetzten PID-Reglers entsprechen nicht der Definition der Nachstellzeit Tn und der Vorhaltzeit Tv. Sie müssen also gesondert gekennzeichnet werden. Dieser PID-Regler ist einfacher zu parametrieren.

Sprungantwort Regelstrecke mit zwei verschiedenen PID-Reglerstrukturen

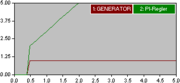
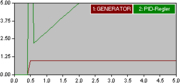
Das grafische Beispiel der Sprungantwort eines Regelkreises mit PID-Regler-Parametrierung und Nullstellen- Polstellenkompensation zeigt (in der Bildvergrößerung) diese unterschiedlichen Probleme an. Zum einfacheren Verständnis wurde der ideale PID-Regler dargestellt.

In der Simulation der dargestellten Sprungantwort spielen hohe Amplituden des Reglerausgangs keine Rolle. Eine Signalbegrenzung des Reglerausgangs und möglichst mit Begrenzung des I-Anteils führt zu einem langsameren Anstieg der Sprungantwort und besserer Dämpfung des Regelkreises. Das Einfügen einer kleinen parasitären Zeitverzögerung führt zu größeren Überschwingungen und schlechterer Dämpfung.

Zusammenfassung der Eigenschaften des PID-Reglers:

• Er ist von den Standard-Reglern am anpassungsfähigsten, hat keine bleibende Regelabweichung bei Führungs- und Störgrößensprung und kann zwei Verzögerungen (T1-Glieder) der Regelstrecke kompensieren und damit die Regelstrecke vereinfachen.
• Nachteilig ist durch das I-Glied bedingt, dass eine zusätzliche Polstelle mit −90° Phasenwinkel in dem offenen Regelkreis eingefügt wird, was eine Reduzierung der Kreisverstärkung KPID bedeutet. Deshalb ist der PID-Regler (wie auch der PI-Regler) kein schneller Regler.
• Es gibt nur drei Einstellparameter, KPID, T1 (bzw. TN), T2 (bzw.TV) des idealen Reglers.
• Er kann eine Regelstrecke mit drei dominanten Zeitkonstanten von T1-Gliedern regeln, wenn die Kreisverstärkung reduziert wird und die längere Dauer des Einschwingens der Regelgröße auf den Sollwert akzeptiert wird. Dabei kann mit KPID jeder gewünschte Dämpfungsgrad D eingestellt werden, von aperiodisch (D=1) bis schwach gedämpft schwingend (D gegen 0).
• Er kann eine Regelstrecke mit I-Glied und einem T1-Glied optimal regeln.
• Der PID-Regler ist an einer Regelstrecke mit dominanter Totzeit ungeeignet.

Entwurf und Realisierung

Übliche Testsignale für Regelkreisglieder sind:

• Eingangssprung (Sprungantwort)
• Anstiegsfunktion
• Stoßfunktion (Deltafunktion)

Für den Entwurf von P-, PI-, PD- und PID-Reglern können das Wurzelortskurvenverfahren und das Frequenzkennlinienverfahren eingesetzt werden. Hierzu muss ein Modell der Regelstrecke als LZI-System vorliegen. Welcher Regler zum Einsatz kommt, hängt ganz von den Eigenschaften der Regelstrecke ab. Es ist zu klären:

• Anzahl der Verzögerungsglieder, Anzahl der zugehörigen dominanten Zeitkonstanten;
• ist eine Totzeit vorhanden?
• liegt eine Sprungantwort der Regelstrecke vor, die sich als Ersatztotzeit mit Ersatzzeitkonstante definieren lässt?
• enthält die Strecke ein I-Glied oder ein instabiles T1-Glied?

Ist dies nicht der Fall, können Faustformelverfahren herangezogen werden.

Heute werden zur Realisierung zumeist digitale Regler angewandt, sodass die kontinuierlichen Regler in zeitdiskrete Regler umzurechnen sind.

Regler höherer Ordnung

Bei komplexen Systemen kann es notwendig werden, Regler höherer Ordnung einzusetzen.

Statische lineare Rückführungen

Zustandsrückführung

Zustandsrückführung mit Vorfilter $\mathbf{V}$.

Die Zustandsrückführung ist eine Mehrgrößenregelung, bei welcher der Zustandsvektor 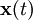$\mathbf{x}(t)$ mittels Matrixverstärkung 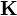$\mathbf{K}$ auf den Eingang zurückgeführt wird: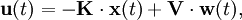

$\mathbf{u}(t) = -\mathbf{K}\cdot\mathbf{x}(t) + \mathbf{V}\cdot \mathbf{w}(t),$

wobei 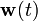$\mathbf{w}(t)$ den Sollwert bezeichnet, der über ein Vorfilter 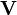$\mathbf{V}$ aufgeschaltet wird, um eine möglicherweise bleibende Regelabweichung zu kompensieren (siehe Bild).

Ist die Regelstrecke ein lineares System, so ergibt sich das folgende Zustandsraummodell des geschlossenen Regelkreises zu

$\dot{\mathbf{x}}(t) = \mathbf{(A-BK)x}(t) + \mathbf{BVw}(t)$

$\mathbf{y}(t) = \mathbf{(C-DK)x}(t) + \mathbf{DVw}(t).$

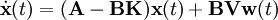
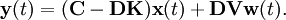
Für Zustandsrückführungen gibt es im wesentlichen zwei Entwurfsverfahren. Beim Reglerentwurf zur Polzuweisung (engl. pole placement) werden für ein Mehrgrößensystem gewünschte Eigenwerte des Regelkreises durch die Rückführung festgelegt. Die Güteforderungen aus dem Zeitbereich werden in die Lage der Eigenwerte übersetzt. Die Pole können genau dann beliebig vorgegeben werden, wenn die zu regelnde Strecke vollständig steuerbar ist. Andernfalls gibt es einzelne feste Eigenwerte, die nicht verändert werden können.

Auch der Entwurf eines LQ-Reglers, ein Verfahren zur optimalen Regelung, basiert auf der Struktur der Zustandsrückführung. Jedes Entwurfsverfahren muss auf eine stabile Matrix 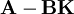$\mathbf{A-BK}$ führen, damit der Regelkreis stabil ist.

Die Zustandsrückführung erfordert die Kenntnis des Zustandes zu jedem Zeitpunkt. Ist die Regelstrecke beobachtbar, so kann der Zustandsvektor durch Einsatz eines Beobachters aus den Ausgangsgrößen rekonstruiert werden.

Ausgangsrückführung

Ausgangsrückführung mit Vorfilter $\mathbf{V}$

Bei nicht beobachtbaren Strecken stellt der Entwurf einer Ausgangsrückführung

$\mathbf{u}(t) = -\mathbf{K}\cdot\mathbf{y}(t) + \mathbf{V}\cdot \mathbf{w}(t),$

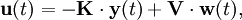
eine Alternative dar. Unter scharfen Voraussetzungen kann eine Zustandsrückführung durch eine Ausgangsrückführung ersetzt werden, ohne die Lage der erreichten Eigenwerte zu verändern. Zumeist muss man jedoch Verschiebungen der gewünschten Pole durch die Ersetzung in Kauf nehmen.

Ist die Regelstrecke ein lineares System, so lautet das Zustandsraummodell des geschlossenen Regelkreises mit Ausgangsrückführung

$\dot{\mathbf{x}}(t) = \mathbf{(A-BKC)x}(t) + \mathbf{BVw}(t)$

$\mathbf{y}(t) = \mathbf{(C-DKC)x}(t) + \mathbf{DVw}(t).$

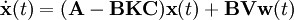
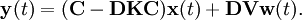
Für einen stabilen Regelkreis muss die Matrix 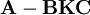$\mathbf{A-BKC}$ eine stabile Matrix sein.

Nichtlineare Regler

Nichtlineare Regler sind Regler, bei denen die Abbildung der Regeldifferenz auf den Stellwert nichtlinear ist. Hierzu gibt es verschiedene Verfahren.

Adaptive Regler

Hauptartikel: Adaptive Regelung

Adaptive Regler sind Regler, die ihre Parameter automatisch an die Regelstrecke anpassen. Sie sind somit zur Regelung zeitvarianter Regelstrecken geeignet.

Extremwertregler

Hauptartikel: Extremwertregelung

Extremwertregler dienen dazu, den Prozess in einen aus Sicht des Anwenders optimalen Zustand zu führen und dort zu halten. Sie werden dort verwendet, wo sich aus den Messgrößen gegenüber den Stellgrößen ein Kennfeld ergibt, dass ein Extremum aufweist.

Nichtstetige Regler

Nichtstetige Regler sind Regler, bei denen die Abbildung der Regeldifferenz auf den Stellwert Sprünge enthält. Typischerweise ist die Kennlinie stückweise konstant. Gebräuchlich sind Zwei- und Dreipunktregler. Vielfach sind optimale Regler hinsichtlich eines Gütemaßes nichtstetige zeitvariante Regler. So sind z. B. zeitoptimale Regler mit beschränkten Stellsignal Zweipunktregler die mittels des Maximumprinzips konstruiert werden.

Fuzzy-Regler

Hauptartikel: Fuzzy-Regler

Fuzzy-Regler arbeiten mit sogenannten „linguistischen Variablen“, welche sich auf „unscharfe Mengenangaben“ beziehen, wie z. B. hoch, mittel und niedrig. Die „Regelbasis“ verknüpft die fuzzifizierten Ein- und Ausgangssignale mit logischen Regeln wie WENN-Teil und DANN-Teil. Mit der Defuzzifizierung wird die unscharfe Menge wieder in scharfe Stellbefehle gewandelt (z. B. Ventilkombinationen für „Kraft Aufbau“ oder „Kraft Abbau“ oder „Kraft halten“).

Diese Regler gelten als robust und arbeiten auch bei Änderung der Regelstrecken-Parameter zuverlässig. Sie können in Bezug auf Genauigkeit oder Schnelligkeit jedoch keinen angepassten P-, I-, PD-, PI- oder PID-Regler an einer stetigen Regelstrecke ersetzen.

Zweipunktregler

Hauptartikel: Zweipunktregler

Die Zweipunktregler können einfachste Regelaufgaben zufriedenstellend lösen. Sie vergleichen die Regelgröße mit einem meist hysteresebehafteten Schaltkriterium und kennen nur zwei Zustände: meist „Ein“ oder „Aus“. Da ihre Funktion leicht zu durchschauen ist, sind sie das am häufigsten angewendete Verfahren.

Mehrpunktregler

Hauptartikel: Dreipunktregler

Bei Mehrpunktreglern kommen zusätzliche Schaltzustände hinzu (z. B. Heizung, Kühlung). Der Regler wird erweitert auf das Schaltkriterium der Regelgröße mit „größer“, oder „kleiner“ oder „gleich“

Die Regelstrecke bestimmt die Frequenz, mit der die Energieimpulse konstanter Größe wirken. Die Regelgröße schwingt innerhalb der Grenzen eines Toleranzbandes. Mit einer zeitbehafteten Rückführung des Reglerausgangs auf die Regelabweichung kann man die Regelfrequenz beschleunigen und damit das Toleranzband schmälern.

Anforderungen an den Regler

In der Regelungstechnik werden die Regler meist so dimensioniert, dass die Strecke mit dem Regler entweder ein gutes Führungs- oder Störverhalten hat.

Wobei das gut jeweils zu definieren ist, also die maximale Regelabweichung darf bei einer Störung einen bestimmten Wert nicht überschreiten. Zusätzlich kann es weitere gewünschte Eigenschaften geben wie z. B. die Stellgröße darf einen bestimmten Wert nicht überschreiten oder die eingesetzte Energie zur Regelabweichungsbeseitigung soll minimal sein. Für diese komplexen Aufgabenstellungen sind vielfach Normen und Gewichtungsfunktionen äußerst hilfreich.

Führungsverhalten

Das Führungsverhalten gibt an, wie der Regler auf eine Sollwertänderung reagieren soll. Allgemein lässt sich dazu meist sagen, wenn der Sollwert verändert wird, soll der Regler möglichst schnell und präzise den Istwert auf den Sollwert bringen. Wenn es nur auf hohe Geschwindigkeit ankommt, ist der Zweipunktregler nicht zu schlagen.

Störverhalten

Das Störverhalten gibt an, wie der Regler auf eine Veränderung der Störgröße reagieren soll. Allgemein lässt sich zumeist sagen, wenn eine Störung auftritt, die den Istwert verändert, dann soll der Regler möglichst schnell und präzise diese Störung ausregeln und den Ausgangswert auf den Sollwert bringen.

Der Idealfall wäre, wenn

1. Regelgröße = Führungsgröße,
2. die Störungen sofort kompensiert werden (keine Auswirkung auf die Regelgröße).

Normen

Für bestimmte Aufgabenstellungen sind Normen (1-Norm (Abweichung), 2-Norm(Energie), Maximumsnorm (maximale Größe)) oder die mittlere Leistung pow äußerst hilfreich, da sich mit diesen Normen genaue Vorgaben machen lassen und das Ergebnis sich gut überprüfen lässt. Wird Beispielsweise eine Norm x für eine Aufgabenstellung minimiert, so spricht man von einer x-Norm optimalen Regelung.

Gewichtungsfunktionen

Weiterhin kann es für komplexe Aufgabenstellungen hilfreich sein, Gewichtungsfunktionen einzuführen, um zum Beispiel die Stellgröße für hohe Frequenzen möglichst kleine Werte annehmen zu lassen und die Regelabweichung für tiefe Frequenzen klein zu halten. Das bedeutet, dass eine stationäre Genauigkeit mit möglichst kleinen Stellwerten gewährleistet wird. Ohne diese Gewichtungsfunktionen hätte es nur eine Vorgabe für alle Frequenzen geben können.

Realisierung von Reglern

Analogregler und Digitalregler

• Analogrechner zur Darstellung von gewöhnlichen Differentialgleichungen
• Digitalregler mit Signalquantisierung und fester Abtastzeit

Kompaktregler

• Heute zumeist digitale Kleinrechner mit eigenen, genormten elektrischen Ein- und Ausgängen zur Montage auf Hut-Schienen oder als Schalttafeleinbau.

Softregler in Prozessleitsystemen

• Der Regler wird als Computerprogramm in einem hinreichend leistungsfähigen Prozessleitsystem (PLS) realisiert. Die Ausführung des Codes erfolgt in deterministischer Echtzeit. Der Regler benötigt keine direkte Verdrahtung zu Sensoren und Aktoren, sondern kommuniziert mit beliebigen an das PLS angeschlossenen Aktoren und Sensoren, z. B. über ein Feldbussystem wie Profibus, Interbus, Foundation Fieldbus, Aktuator-Sensor-Interface (AS-Interface). Dieses Vorgehen vermindert den Verkabelungsaufwand und erleichtert eine örtliche Trennung von Prozess und Regler.

Universalregler

Regler werden in vielen Lebensbereichen eingesetzt. Oft sind sie in Geräten eingebaut z.B. der Zweipunktregler im elektrischen Bügeleisen, oder einer Schaltung zur Spannungsstabilisierung in einem Netzteil. Diese Regler sind meist speziell für das entsprechende Gerät entwickelt und gestatten keine Parameterveränderungen. In der Prozesstechnik, z.B. Chemieindustrie, Kraftwerke oder Nahrungsmittelindustrie findet man viele Regelungen. Hier werden Universalregler eingesetzt. Universalregler kann man durch Einstellen der Reglerparameter:

• Proportionalbeiwert,
• Nachstellzeit und
• Vorhaltezeit

als P-, PI-, PD- oder PID- Regler betreiben.

Ein Universalregler hat genormte Ein- und Ausgangssignale, sogenannte Einheitssignale. Das Eingangssignal kommt aus dem Messsystem und das Ausgangssignal wirkt auf das Stellglied. So ist es möglich, Geräte verschiedener Hersteller in einem Regelkreis miteinander zu betreiben. Life Zero (lebender Nullpunkt) bedeutet, dass das Einheitssignal einen Wert, z.B. 4mA, hat, wenn der Messwert 0 ist. Ist das Einheitssignal 0mA, muss also ein Drahtbruch oder ein Kurzschluss vorliegen. Bei elektrischen Einheitssignalen werden Stromsignale bevorzugt. Sie sind bei langen Signalleitungen weniger anfällig gegen äußere Störfelder und es tritt kein Spannungsfall auf.

Pneumatischer Regler

• arbeitet mit genormten pneumatischen Ein- und Ausgängen, z.B. 0,2 ... 1 bar oder 3 ... 15 psi. Einsatz in der Verfahrenstechnik z.B. im Explosionsschutz-Bereich.

Regler ohne Hilfsenergie (ROH)

• Regler ohne Hilfsenergie, häufig als ROH bezeichnet, übernehmen alle zur Regelung erforderlichen Aufgaben. Sie integrieren den Messaufnehmer, den Regler und auch das Stellglied in ein System und nehmen die Energie zum Arbeiten aus dem zu regelnden Medium.

Literatur

• Martin Horn, Nicolaos Dourdoumas: Regelungstechnik (2006), Pearson Studium, ISBN 3-8273-7260-7
• O. Föllinger, Regelungstechnik, Einführung in die Methoden und ihre Anwendung, Hüthig Verlag, 1994, ISBN 3-7785-2336-8
• J. Lunze, Regelungstechnik 1 (Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen), Springer-Verlag, 2006, ISBN 3-540-28326-9
• H. Unbehauen, Regelungstechnik 1, Vieweg Verlag, 2007, ISBN 3-528-21332-9

Siehe auch

• Portal: Mess-, Steuerungs- und Regelungstechnik
• Regelungstechnik
• Rückkopplung
• PT1-Glied
• PT2-Glied
• Totzeit-Glied

Siehe jedoch

• Steuerung, Schieberegler

Weblinks

• Regelungstechnik im Roboternetz-Wiki
• Regelungstechnisches Beispiel: Klospülung
• Demo-Version von WinFACT 7 – Demoprogramm, in dem die einzelnen Regler gut erklärt werden (Programmteil: Boris)
• Einführung in die ROH-Technik