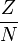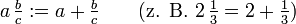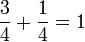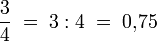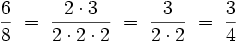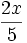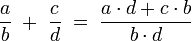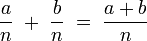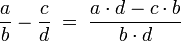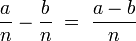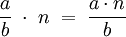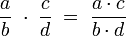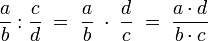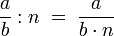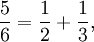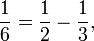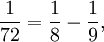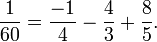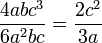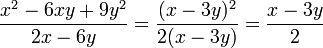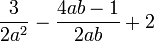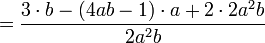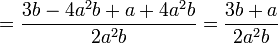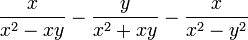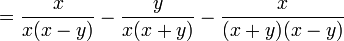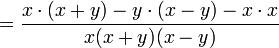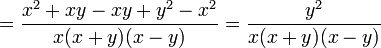¼

Ein Kuchen ist in vier gleiche Teile geteilt. Jeder Teil des Kuchens entspricht ¹⁄₄. Wie man sieht, entsprechen zwei Teile (2 · ¹⁄₄ = ²⁄₄) einem halben (=¹⁄₂) Kuchen.

Die Bruchrechnung befasst sich mit der Division von ganzen Zahlen. Ein Bruch (manchmal auch gewöhnlicher Bruch, englisch vulgar fraction, oder verallgemeinert auf die ganzen Zahlen eine Bruchzahl) ist dabei die Darstellung einer rationalen Zahl als Quotient (d. h. als Ergebnis einer Division), er drückt also ein Verhältnis oder einen Anteil aus.

Definition und Bezeichnungen

Beschreibung eines gemeinen Bruches

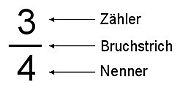
Brüche werden im Allgemeinen durch eine Übereinanderstellung von Zähler und Nenner, getrennt durch einen waagerechten Strich, dargestellt:

$\frac{Z}{N}$

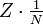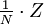der Zähler Z ist dabei der Dividend der Division, der Nenner N ist der Divisor. Jede Division lässt sich als Bruch schreiben. (Strenggenommen gilt dies nur, falls die Multiplikation kommutativ ist, denn in der Bruchschreibweise kann man nicht zwischen $Z \cdot \tfrac 1 N$ und $\tfrac 1 N \cdot Z$ unterscheiden.)

Zähler und Nenner einer konkreten Bruchzahl sind ganze Zahlen, für Brüche im Allgemeinen können sie aber auch algebraische Ausdrücke sein. Dabei darf der Nenner niemals Null sein, da eine Division durch Null nicht definiert ist (und sich nicht sinnvoll definieren lässt).

Ist der Zähler in einem Bruch 1 (z. B. ¹⁄₂ ¹⁄₉), spricht man von einem Stammbruch, alle anderen sind abgeleitete oder Zweigbrüche.

Wenn bei Brüchen der Betrag des Zählers kleiner als der des Nenners ist, so handelt es sich um echte (eigentliche) Brüche (z. B. ⁶⁄₇ oder ²⁄₅), andernfalls um unechte (uneigentliche) Brüche (z. B. ⁷⁄₇ oder ¹¹⁄₃).

Brüche wie ¹²/₃, bei denen der Zähler ein ganzzahliges Vielfaches des Nenners ist, bezeichnet man als Scheinbrüche, da sie sich durch Kürzen in ganze Zahlen umwandeln lassen (im Beispiel in die Zahl 4).

Im Alltag schreibt man auch gemischte Zahlen (gemischte Brüche), also den ganzzahligen Anteil, d. h. die zur Null hin gerundete Zahl, und anschließend den Divisionsrest (kurz Rest) als echten Bruch, zum Beispiel 1¹⁄₃ statt ⁴⁄₃. In manchen Ländern wie Frankreich sind gemischte Zahlen unüblich.

$\textstyle a\,\frac{b}{c} := a + \frac{b}{c} \quad\quad(\text{z. B. } 2\,\frac{1}{3} = 2 + \frac{1}{3})$

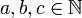für $\quad a, b, c \in \N$ und b < c. Es gilt

$\textstyle a\, \frac{b}{c} = \frac{a\cdot c + b}{c}\textstyle\quad\quad (\text{z. B. } 2\,\frac{1}{3} = \frac{2\cdot 3 + 1}{3} = \frac{7}{3})$.

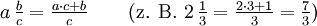Beispiele für Brüche

$\frac{3}{4} + \frac{1}{4} = 1$ Man liest: „drei Viertel plus ein Viertel“

$\frac{2}{3}$

der Bruch mit der 2 im Zähler und der 3 im Nenner bedeutet „zwei Drittel“, also zwei Teile eines in drei gleichgroße Teile geteilten Ganzen.

$\frac{3}{4}$

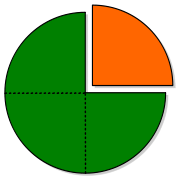
bedeutet entsprechend „drei Viertel“.

Es ist hierbei implizit verstanden, dass „ein Ganzes“ aus „drei (gleich großen) Dritteln“, „vier (gleich großen) Vierteln“ usw. besteht. Somit wird klar, dass man einen Bruch auch als eine rationale Zahl auffassen kann, die man bei der Division des Zählers durch den Nenner erhält.

$\frac{3}{4} \; = \; 3 : 4 \; = \; 0{,}75$

Brüche können gekürzt werden, wenn Zähler und Nenner mindestens einen gemeinsamen ganzzahligen Teiler haben. Dabei ist es hilfreich, wenn man den Zähler und den Nenner in ihre Primfaktoren zerlegt.

$\frac{6}{8} \; = \; \frac{2 \cdot 3}{2 \cdot 2 \cdot 2} \; = \; \frac{3}{2 \cdot 2} \; = \; \frac{3}{4}$

Auch algebraische Ausdrücke, die Variablen enthalten, kann man als Bruch schreiben:

$\frac{2x}{5}$

bedeutet „zwei x geteilt durch Fünf“.

Rechenregeln

Addition

$\frac{a}{b} \; + \; \frac{c}{d} \; = \; \frac{a \cdot d + c \cdot b}{b \cdot d}$

Addition von gleichnamigen Brüchen:

$\frac{a}{n} \; + \; \frac{b}{n} \; = \; \frac{a + b}{n}$

Subtraktion

$\frac{a}{b} - \frac{c}{d} \; = \; \frac{a \cdot d - c \cdot b}{b \cdot d}$

Subtraktion von gleichnamigen Brüchen:

$\frac{a}{n} - \frac{b}{n} \; = \; \frac{a - b}{n}$

Multiplikation

$\frac{a}{b} \; \cdot \; n \; = \; \frac{a \cdot n}{b}$

$\frac{a}{b} \; \cdot \; \frac{c}{d} \; = \; \frac{a \cdot c}{b \cdot d}$

Division

Klassisches Beispiel

$\frac{a}{b} : \frac{c}{d} \; = \; \frac{a}{b} \; \cdot \; \frac{d}{c} \; = \; \frac{a \cdot d}{b \cdot c}$

Man dividiert also durch einen Bruch, indem man mit dem Kehrwert des Bruches multipliziert. Die Division wird also auf die Multiplikation zurückgeführt.

$\frac{a}{b} : n \; = \; \frac{a}{b \cdot n}$

Potenzen

Regel	Beispiel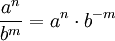
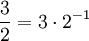
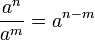
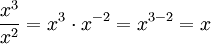
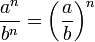
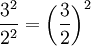
$\frac{a^n}{b^m} = a^n \cdot b^{-m}$	$\frac{3}{2} = 3 \cdot 2^{-1}$
$\frac{a^n}{a^m} = a^{n-m}$	$\frac{x^3}{x^2} = x^3 \cdot x^{-2} = x^{3-2} = x$
$\frac{a^n}{b^n} = \left(\frac{a}{b}\right)^n$	$\frac{3^2}{2^2} = \left(\frac{3}{2}\right)^2$

Kürzen und Erweitern

Kürzen $\rightarrow$
$\frac{a \cdot c}{b \cdot c} \; = \; \frac{a}{b}$
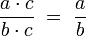
$\leftarrow$ Erweitern

Einige hilfreiche Eselsbrücken in diesem Zusammenhang sind:

• Faktoren kürzen, das ist brav; wer Summen kürzt, der ist ein Schaf.
• Differenzen und Summen kürzen nur die Dummen.
• Was du oben tust, machst du auch unten!

Aus der Äquivalenz 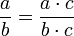$\frac a b = \frac{a\cdot c}{b\cdot c}$ für beliebige natürliche Zahlen c > 0 folgt, dass jede rationale Zahl durch unendlich viele verschiedene Brüche dargestellt werden kann, denn es gilt $\frac{a}{b}=\frac{2a}{2b}=\frac{3a}{3b}=\frac{4a}{4b}=\dots$.

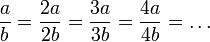Weitere Darstellungsformen

Brüche kann man oft in so genannte Partialbrüche zerlegen, deren Nenner ganze Potenzen von Primzahlen sind; z. B.:

$\frac{5}{6} = \frac{1}{2} + \frac{1}{3} ,$

$\frac{1}{6} = \frac{1}{2} - \frac{1}{3} ,\,$

$\frac{1}{72} = \frac{1}{8} - \frac{1}{9} ,$

$\frac{1}{60} = \frac{-1}{4} - \frac{4}{3} + \frac{8}{5}.$

Es gibt auch Zerlegungen als so genannte ägyptische Brüche (Stammbrüche), z. B.

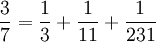$\frac{3}{7} = \frac{1}{3} + \frac{1}{11} + \frac{1}{231}$ und

$\frac{25}{31} = \frac{1}{2} + \frac{1}{4} + \frac{1}{18} + \frac{1}{1116}$,

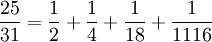die alten Ägypter kannten nur solche Summen und haben mit diesen gerechnet.

Das Zahlentripel 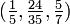$(\tfrac{1}{5},\tfrac{24}{35}, \tfrac{5}{7})$ ist ein Beispiel eines pythagoreischen Bruchs (siehe auch pythagoreisches Tripel), denn

$\left(\frac{1}{5}\right)^2 + \left(\frac{24}{35}\right)^2 = \left(\frac{5}{7}\right)^2$.

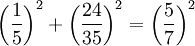Rechnen mit Bruchtermen

Bruchterme, also Rechenausdrücke in der Form von Brüchen, spielen in der elementaren Algebra eine wichtige Rolle. Im Allgemeinen enthalten Bruchterme neben Zahlen auch Variable. Die Verfahren des Rechnens mit Bruchzahlen lassen sich auf Bruchterme übertragen.

Definitionsbereich eines Bruchterms

Bei der Bestimmung des Definitionsbereiches eines Bruchterms ist zu beachten, dass der Nenner nicht den Wert 0 haben darf. Beispielsweise wäre der von x abhängige Bruchterm 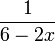$\frac{1}{6-2x}$ beim Einsetzen von x = 3 nicht definiert. Der Definitionsbereich ist also 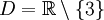$D = \mathbb{R}\setminus\{3\}$, wenn als Grundmenge die Menge der reellen Zahlen vorausgesetzt wird. In komplizierteren Fällen sollte der Nenner in Faktoren zerlegt werden, damit der Definitionsbereich erkennbar wird.

Beispiel: 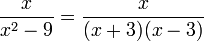$\frac{x}{x^2-9} = \frac{x}{(x+3)(x-3)}$ hat den Definitionsbereich $D = \mathbb{R} \setminus \{-3; +3\}$.

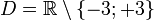Kürzen von Bruchtermen

Kürzen bedeutet, dass man Zähler und Nenner durch denselben Rechenausdruck dividiert. Wichtig dabei ist, dass nur Faktoren von Produkten herausgekürzt werden können. Summen und Differenzen im Zähler und im Nenner müssen gegebenenfalls zuerst in Produkte zerlegt werden (Faktorisierung).

Beispiele:

$\frac{4abc^3}{6a^2bc} = \frac{2c^2}{3a}$

$\frac{x^2-6xy+9y^2}{2x-6y} = \frac{(x-3y)^2}{2(x-3y)} = \frac{x-3y}{2}$

Addition und Subtraktion von Bruchtermen

Wie bei Zahlen ist es nötig, die gegebenen Bruchterme gleichnamig zu machen, d.h. auf den gleichen Nenner zu bringen. Man bestimmt einen möglichst einfachen gemeinsamen Nenner (Hauptnenner), der durch alle gegebenen Nenner teilbar ist.

Beispiel:

$\frac{3}{2a^2} - \frac{4ab-1}{2ab} + 2$

Als Hauptnenner ergibt sich 2a²b. Die Erweiterungsfaktoren der drei gegebenen Bruchterme erhält man dadurch, dass man jeweils den gefundenen Hauptnenner durch den bisherigen Nenner dividiert. Die Erweiterungsfaktoren sind also b, a und 2a²b.

$\frac{3}{2a^2} - \frac{4ab-1}{2ab} + 2$

$= \frac{3 \cdot b - (4ab-1) \cdot a + 2 \cdot 2a^2b}{2a^2b}$

$= \frac{3b-4a^2b+a+4a^2b}{2a^2b} = \frac{3b+a}{2a^2b}$

Häufig lässt sich der Hauptnenner nur erkennen, wenn man die Nenner in Faktoren zerlegt (Faktorisierung). Dabei greift man oft auf die Methode des Ausklammerns zurück oder verwendet binomische Formeln.

Beispiel:

$\frac{x}{x^2-xy} - \frac{y}{x^2+xy} - \frac{x}{x^2-y^2}$

$= \frac{x}{x(x-y)} - \frac{y}{x(x+y)} - \frac{x}{(x+y)(x-y)}$

$= \frac{x \cdot (x+y) - y \cdot (x-y) - x \cdot x}{x(x+y)(x-y)}$

$= \frac{x^2 + xy - xy + y^2 - x^2}{x(x+y)(x-y)} = \frac{y^2}{x(x+y)(x-y)}$

Multiplikation und Division von Bruchtermen

Beim Multiplizieren von Bruchtermen müssen sowohl die Zähler als auch die Nenner multipliziert werden. Gemeinsame Faktoren von Zähler und Nenner sollten herausgekürzt werden.

Beispiel: $\frac{4xy}{z^2} \cdot \frac{xz}{6y} = \frac{4x^2yz}{6yz^2} = \frac{2x^2}{3z}$

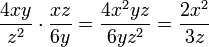
In komplizierteren Aufgaben sollte man Zähler und Nenner in Faktoren zerlegen, um sie bereits vor der eigentlichen Multiplikation herauskürzen zu können.

Beispiel: $\frac{a-2b}{4a+1} \cdot \frac{16a^2-1}{a^2-4ab+4b^2} = \frac{a-2b}{4a+1} \cdot \frac{(4a+1)(4a-1)}{(a-2b)^2} = \frac{4a-1}{a-2b}$

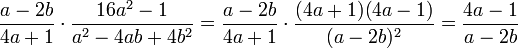
Die Division von Bruchtermen lässt sich auf die Multiplikation zurückführen. Man dividiert durch einen Bruchterm, indem man mit seinem Kehrwert multipliziert.

Beispiel: $\frac{2x-3}{5x} : \frac{4x^2-9}{10x^2} = \frac{2x-3}{5x} \cdot \frac{10x^2}{(2x+3)(2x-3)} = \frac{2x}{2x+3}$

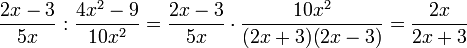
Siehe auch

• Kettenbruch
• Farey-Reihe

Weblinks