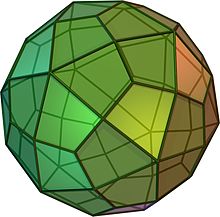
Deltoidalhexakontaeder

3D-Ansicht eines Deltoidalhexakontaeders (Animation)

Das Deltoidalhexakontaeder ist ein konvexes Polyeder, das sich aus 60 Deltoiden zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum Rhombenikosidodekaeder und hat 62 Ecken sowie 120 Kanten.

Entstehung

Konstruktion des Deltoids am Rhombenikosidodekaeder

Durch Verbinden der Mittelpunkte vierer Kanten, die in jeder Raumecke des Rhombenikosidodekaeders zusammenstoßen, entsteht ein Trapez, dessen Umkreis gleichzeitig Inkreis des Deltoids, der Begrenzungsfläche des Deltoidalhexakontaeders, ist. Bei diesem speziellen Typ sind alle Flächenwinkel gleich groß (≈ 154°), und es existiert ein einheitlicher Kantenkugelradius.

Sei d die Kantenlänge des Rhombenikosidodekaeders, so sind die resultierenden Seitenlängen des Deltoids gegeben durch

$a = \, \frac{d}{3}\, \sqrt{25 - 5\sqrt{5}}$

$b = \, \frac{d}{11}\, \sqrt{5 \,(85 - 31\sqrt{5})}$

Formeln

Nachstehend aufgeführte Formeln gelten ausschließlich für den Spezialfall $b = \tfrac{3}{22} \, a \, (7 - \sqrt{5})$.

Für das Polyeder

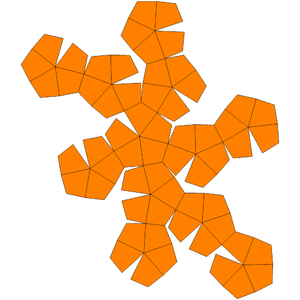Netz des Deltoidalhexakontaeders

Größen eines Deltoidalhexakontaeders mit Kantenlänge a
Volumen	$V = \frac{45}{11} \,a^3 \sqrt{\frac{370 + 164\sqrt{5}}{25}}$
Oberflächeninhalt	$O = \frac{9}{11} \,a^2 \sqrt{10\,(157 + 31\sqrt{5})}$
Inkugelradius	$\rho = \frac{3}{2} \,a\, \sqrt{\frac{135 + 59\sqrt{5}}{205}}$
Kantenkugelradius	$r = \frac{3}{20} \,a\, (5+ 3\sqrt{5})$
Flächenwinkel  ≈ 154,12°	$\cos \, \alpha= -\frac{1}{41}\,(19 + 8\sqrt{5})$
3D-Kantenwinkel  ≈ 153,44°	$\cos \, \gamma = -\frac{2}{\sqrt{5}}$

Für das Deltoid

Größen des Drachenvierecks
Flächeninhalt	$A = \frac{3}{22} \,a^2 \sqrt{\frac{157 + 31\sqrt{5}}{10}}$
2. Seitenlänge	$b = \frac{3}{22} \,a\, (7 - \sqrt{5})$
Kurze Diagonale	$e = 3a\, \sqrt{\frac{5 - \sqrt{5}}{20}}$
Lange Diagonale	$f = \frac{a}{11} \sqrt{\frac{470 + 156\sqrt{5}}{5}}$
Inkreisradius	$r = \frac{3}{10} \,a\, \sqrt{\frac{5\,(17+5\sqrt{5})}{82}}$
Seitenwinkel  ≈ 86,97°	$\cos \, \alpha = \frac{1}{10}\,(5 - 2\sqrt{5})$
Fußwinkel  ≈ 67,78°	$\cos \, \beta = \frac{1}{40}\,(9\sqrt{5} - 5)$
Kopfwinkel  ≈ 118,27°	$\cos \, \gamma = -\frac{1}{20}\,(5 + 2\sqrt{5})$

Weblinks

• Eric W. Weisstein: Deltoidalhexakontaeder. In: MathWorld. (englisch)

Platonische Körper

Tetraeder · Würfel · Oktaeder · Dodekaeder · Ikosaeder