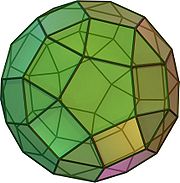
Kleines Rhombenikosidodekaeder

Rhombenikosidodekaeder

Das (kleine) Rhombenikosidodekaeder ist ein Polyeder, das zu den archimedischen Körpern zählt. Es besteht aus 20 regulären Dreiecken, 30 Quadraten und 12 regelmäßigen Fünfecken.

Der Name des Rhombenikosidodekaeders beruht auf der Tatsache, dass die 30 Quadrate deckungsgleich zu den 30 Rhomben eines umbeschriebenen Rhombentriakontaeders sind. Der zum Rhombenikosidodekaeder duale Körper ist das Deltoidalhexakontaeder.

Formeln

Größen eines Rhombenikosidodekaeders mit der Kantenlänge a
Volumen	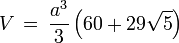$V \, = \, \frac{a^3}{3} \left(60 + 29\sqrt{5} \right)$
Oberflächeninhalt	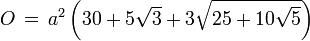$O \, = \, a^2 \left(30+5\sqrt{3}+ 3\sqrt{25+ 10\sqrt{5}} \right)$
Umkugelradius	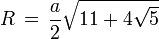$R \, = \, \frac{a}{2} \sqrt{11+ 4\sqrt{5}}$
Kantenkugelradius	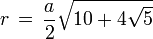$r \, = \, \frac{a}{2} \sqrt{10+ 4\sqrt{5}}$

Weblinks

• Eric W. Weisstein: Small Rhombicosidodecahedron auf MathWorld (engl.)

Platonische Körper

Tetraeder | Würfel | Oktaeder | Dodekaeder | Ikosaeder

 

Archimedische Körper

Tetraederstumpf · Kuboktaeder · Hexaederstumpf · Oktaederstumpf · Rhombenkuboktaeder · Großes Rhombenkuboktaeder · Dodekaederstumpf · Ikosaederstumpf · Ikosidodekaeder · Abgeschrägtes Hexaeder · Rhombenikosidodekaeder · Großes Rhombenikosidodekaeder · Abgeschrägtes Dodekaeder 

 

Catalanische Körper

Rhombendodekaeder · Triakistetraeder · Triakisoktaeder · Tetrakishexaeder · Deltoidalikositetraeder · Pentagonikositetraeder · Rhombentriakontaeder · Hexakisoktaeder · Triakisikosaeder · Pentakisdodekaeder · Deltoidalhexakontaeder · Pentagonhexakontaeder · Disdyakistriakontaeder