Mechanisches Filter

Ein mechanisches Filter ist im Rahmen der Signalverarbeitung ein analoges Filter welches ähnlich wie elektrische Filter zur Auswahl und Unterdrückung bestimmter Frequenzanteile aus dem Spektrum eines Signals verwendet wird. Im Gegensatz zu elektrischen Filtern wird die Filterwirkung durch mechanische Vibrationen entsprechend gestalteter Massen erzielt. Mechanische Filter zählen zu dem Bereich der Akustik, auch wenn die damit verarbeiteten Frequenzen nicht hörbar sein müssen. Die Schnittstelle zwischen elektrischen und mechanischen System stellen Wandler dar, welche am Eingang die zugeführten elektrische Schwingungen in mechanische Vibrationen, und am Ausgang die mechanischen Schwingungen zurück in elektrische Schwingungen umwandeln.

Allgemeines

Mechanisches Zwischenfrequenzfilter für 455 kHz aus einem Radioempfänger

Zur Berechnung mechanischer Filter können direkt die Methoden und mathematischen Verfahren aus der elektrischen Schaltungstechnik herangezogen werden. Insbesondere können damit die aus der elektrischen Netzwerkanalyse bekannten und etablierten Filterentwurfsmethoden wie auch die Methoden mit Zweitoren direkt in entsprechende mechanische Systeme übertragen werden.

Als Material findet in mechanischen Filtern neben Stahl und verschiedenen Metalllegierungen wie Eisen-Nickel-Legierungen auch keramische Werkstoffe oder Quarz Anwendung. Mechanische Filter werden weiters nach Aufbau und Anwendung unterteilt, wie beispielsweise die akustischen Oberflächenwellen-Filter (SAW-Filter), in der Mikrosystemtechnik (MEMS) miniaturisierte Filter und die im Rückkoppelkreis in Resonanzkreisen eingesetzten Schwingquarze und Keramikresonatoren.

In mechanischen Filtern lassen sich im Vergleich zu passiven analogen Filtern sehr hohe Filtergüten realisieren. Dies folgt aus dem Umstand, dass sich in elektrischen Systemen Spulen mit hoher Induktivität und gleichzeitig sehr geringen ohmschen Widerständen, welche Verluste darstellen, nicht herstellen lassen. Mit mechanischen Filtern und deren vergleichsweise hohen Gütefaktor Q, Werte über 10.000 sind üblich, sind Resonanzkreise mit hoher Frequenzselektivität realisierbar. Diesem Umstand verdankt auch der Schwingquarz in elektrischen Schwingkreisen zur Frequenzerzeugung, beispielsweise in Quarzuhren, seine gegenüber LC-Schwingkreisen hohe Frequenzstabilität und Ganggenauigkeit.^[1]

Geschichtliche Entwicklung

Mechanisches Filter und dessen elektrische „Ersatzschaltung“ aus einem Grammophon

Mechanische Filter sind nicht zwangsläufig auf eine elektrische Schnittstelle und die dafür nötigen Wandler angewiesen. So kann beispielsweise die Berechnung von Lautsprecheboxen ohne dem elektrischen System erfolgen. Die ersten mechanischen Filter wurden in den 1920 Jahren bei dem damals aufkommenden Grammophon auch als reine mechanische Systeme, ohne elektrischer Schnittstelle, entwickelt.^[2]

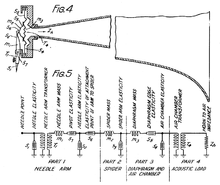
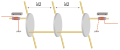
In den 1950 Jahren wurden begonnen mechanische Filter wegen der hohen Gütefaktoren gegenüber LC-Filtern als eigeneständiges Filtermodul, wie in obiger Abbildung als Zwischenfrequenzfilter für 455 kHz dargestellt, in den damaligen Radiogeräten zu realisieren.

Elektrische Wandler

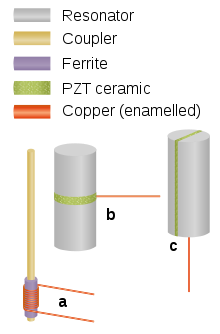Verschiede Wandlertypen. (a) Ein Metallstab aus magnetoresistiven Material. (b) und (c) Zylindrischer Resonanzwandler aus grün dargestellten Piezometerial welches zwischen den Elektroden eingebettet ist für longitudinale und transversale Wellen.

Die elektrischen Wandler in mechanischen Filtern basieren üblicherweise auf zwei Effekten, wenngleich Wandler nicht darauf limitiert sind: Magnetostriktion und Piezoelektrizität. Bei dem quantenmechanischen Effekt der Magnetostriktion nutzt man den Umstand, dass der magnetische Fluss durch ein entsprechendes Material zu einer Längenänderung führt. Meist ist dafür zusätzlich noch eine „magnetische Vorspannung“ in Form eines Dauermagneten notwendig, weshalb in neueren und kleineren Wandlern fast ausschließlich piezoelektrische Wandler aus dem Material Blei-Zirkonat-Titanat (PZT) oder Quarz zur Anwendung kommen. Außerdem kann bei diesen Wandlertypen das piezoelektrische Material als wesentlicher Teil des mechanischen Filtersystem integriert werden, wie dies beispielsweise bei SAW-Filtern, oder bei Resonatoren wie den Schwingquarzen, der Fall ist.

Aufbau

Mechanische Filter zählen zu den passiven Filtern. Elektrische passive Filter werden aus ohmschen Widerständen mit einem elektrischen Widerstand, Kondensatoren mit einer elektrischen Kapazität und Spulen mit einer Induktivität gebildet. Im mechanischen System entspricht dem elektrischen Widerstand R die Dämpfung (D), die Kapazität C die mechanische Nachgiebigkeit (δ), diese Größe ist der Kehrwert der mechanischen Steifigkeit S, und die Induktivität wird durch die Masse M ausgedrückt. Das mechanische Gegenstück zur elektrischen Spannung (U) stellt die mechanische Kraft (F) dar, der elektrische Strom (I) wird durch die Geschwindigkeit (v) repräsentiert.

Aus dieser Analogiebeziehungen lässt sich wie in elektrischen System eine mechanische Impedanz (Z) als Funktion der Kreisfrequenz ω bestimmten, wobei die Kreisfrequenz mit der imaginären Einheit j multipliziert wird. Die Bezeichner x, v, und a stehen für den Abstand x, Geschwindigkeit v und Beschleunigung a. In Summe ergeben sich damit folgende Beziehungen:

Mechanische Größe	Beziehung	Mechanische Impedanz	Elektrische Analoggröße	Elektrische Impedanz
Nachgiebigkeit δ	$\delta = {x \over F}$	$Z = {1 \over \mathrm{j}\omega\delta}$	Kapazität C	$Z_e ={1 \over j \omega C}$
Masse M	$M = \frac{F}{dv/dt} = {F \over a}$	$Z= \mathrm{j} \omega M \,$	Induktivität L	$Z_e= \mathrm{j} \omega L \,$
Dämpfung D	$D = {F \over v}$	$Z = D \,$	Widerstand R	$Z_e = R\,$

Die obige Tabelle stellt die so genannte Impedanzanalogie dar, mit deren Hilfe das mechanische System wie eine elektrische Schaltung beschrieben und berechnet werden kann. Es lassen sich damit auch unmittelbar die Methoden der komplexen Wechselstromrechnung auf das mechanische System anwenden. Jedes mechanisches Element besteht neben einen dämpfenden Anteil zufolge Reibung sowohl aus einer Masse und einer bestimmten Steifigkeit, womit sich wie bei den elektrischen Schaltungen konzentrierte Bauelemente mit einer der gewünschten Eigenschaften nur in Näherung bilden lassen. Überwiegt bei kleiner Dämpfung der Einfluss der Nachgiebigkeit gegenüber der Masse werden „mechanische Kondensatoren“ gebildet. Typischerweise bestehen diese aus dünnen, möglichst langen Stäben. „Mechanische Spulen“, als Gegenstück, bestehen aus kurzen, flachen Scheiben aus massiven Material, welche so ihre Masse maximieren und die Nachgiebigkeit minimieren.

• Prinzipdarstellungen von mechanischen Filtern
• 

  Scheibenförmige Resonatoren und am Rand angebrachte Verbindungselementen mit halber Wellenlänge

• 

  Mechanisches Filter mit Torsions-Resonatoren

• 

  Mechanisches Filter mit Drumhead-Resonatren

• 

  Mechanisches Filter mit Flexual-Resonatoren

Literatur

• Rüdiger G. Ballas, Günther Pfeifer, Roland Werthschützky: Elektromechanische Systeme in Mikrotechnik und Mechatronik. 2. Auflage. Springer, 2009, ISBN 978-3-540-89317-2.

Einzelnachweise

1. ↑ Joseph J. Carr: RF Components and Circuits. Newnes, 2002, ISBN 0-7506-4844-9..
2. ↑ Frederick V. Hunt: Electroacoustics: the Analysis of Transduction, and its Historical Background. Harvard University Press, Cambridge 1954, OCLC 2042530.

Weblinks

 Commons: Mechanical filters – Sammlung von Bildern, Videos und Audiodateien