- Logarithmische Verteilung
-
Die logarithmische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung und kommt aus dem Bereich der Versicherungsmathematik. Sie ist interessant als Schadenshöhenverteilung, wird aber kaum zur Bestimmung der Schadensanzahlen benutzt.
Inhaltsverzeichnis
Definition
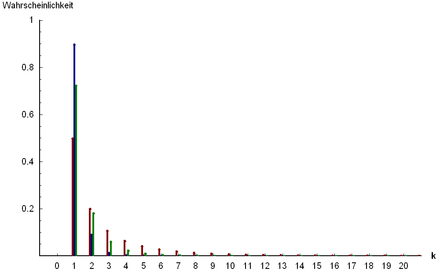
Eine diskrete Zufallsgröße Xn genügt der logarithmischen Verteilung mit den Parametern k (Anzahl der Versuche) und p (Erfolgswahrscheinlichkeit), wenn sie die Wahrscheinlichkeit
besitzt.
Eigenschaften
Erwartungswert
Die logarithmische Verteilung hat einen Erwartungswert von
 .
.
Varianz
Die Varianz bestimmt sich zu
 .
.
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man sofort den Variationskoeffizienten
 .
.
Schiefe
Die Schiefe ergibt sich zu:
 .
.
Charakteristische Funktion
Die charakteristische Funktion hat die Form
 .
.
Erzeugende Funktion
Für die erzeugende Funktion erhält man.
 .
.
Momenterzeugende Funktion
Die momenterzeugende Funktion der logarithmischen Verteilung ist
 .
.
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
Logarithmische Darstellung — Verteilung der Beitragszahlen der aktivsten Autoren in der deutschsprachigen Wikipedia Die logarithmische Darstellung basiert auf einer Skale, die nicht den Wert einer physikalischen Größe verwendet, sondern den Logarithmus ihres Zahlenwerts. Bei … Deutsch Wikipedia
Logarithmische Normalverteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Logarithmische Gammaverteilung — Die Logarithmische Gammaverteilung (auch Log Gammaverteilung) ist eine stetige Wahrscheinlichkeitsverteilung. Sie ist geeignet zur Modellierung von Schadensdaten im extremen Großschadenbereich der Industrie , Haftpflicht , Rückversicherung.… … Deutsch Wikipedia
logarithmische Normalverteilung — logaritminis normalusis skirstinys statusas T sritis fizika atitikmenys: angl. logarithmic normal distribution; lognormal distribution vok. logarithmische Normalverteilung, f; lognormale Verteilung, f; Lognormalverteilung, f rus. логарифмически… … Fizikos terminų žodynas
Logarithmische Rendite — Die logarithmierte Rendite (auch stetige Rendite genannt) ist eine finanzmathematische Größe, die vor allem im Risikomanagement bei der Berechnung von Volatilitäten (z.B. im klassischen Black Scholes Modell der Optionspreisbewertung) eine Rolle… … Deutsch Wikipedia
Lognormal-Verteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Lognormale Verteilung — Die logarithmische Normalverteilung (kurz Log Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X, wenn ln(X) normalverteilt… … Deutsch Wikipedia
Benfordsche Verteilung — Das benfordsche Gesetz, auch Newcomb Benford’s Law (NBL) beschreibt eine Gesetzmäßigkeit in der Verteilung der Ziffernstrukturen von Zahlen in empirischen Datensätzen, zum Beispiel ihrer ersten Ziffern. Es lässt sich etwa in Datensätzen über… … Deutsch Wikipedia
Gauss-Verteilung — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia
Gausssche Verteilung — Dichten normalverteilter Zufallsgrößen Die Normal oder Gauß Verteilung (nach Carl Friedrich Gauß) ist ein wichtiger Typ kontinuierlicher Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß Funktion, Gauß Kurve, Gauß… … Deutsch Wikipedia