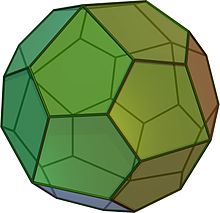
Pentagonikositetraeder

3D-Ansicht eines Pentagonikositetraeders (Animation)

Netz des Pentagonikositetraeders

Das Pentagonikositetraeder ist ein chirales Polyeder, das sich aus 24 unregelmäßigen Fünfecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum abgeschrägten Hexaeder und hat 38 Ecken sowie 60 Kanten.

Die folgenden Bilder zeigen zwei zueinander spiegelbildliche Pentagonikositetraeder.

• 

  Spiegelvariante 1

• 

  Spiegelvariante 2

Entstehung

Konstruktion des Tangentenfünfecks am abgeschrägten Hexaeder

Durch Verbinden der Mittelpunkte von jeweils fünf Kanten, die in jeder Raumecke des abgeschrägten Hexaeders zusammenstoßen, entsteht ein Sehnenfünfeck, dessen Umkreis gleichzeitig Inkreis des Tangentenfünfecks, der Begrenzungsfläche des Pentagonikositetraeders, ist. Bei diesem speziellen Typ sind alle Flächenwinkel gleich groß (≈ 136°), und es existiert ein einheitlicher Kantenkugelradius.

Nachfolgend bezeichne der Term t den Kosinus des kleineren Zentriwinkels ζ im zuvor erwähnten Sehnenfünfeck.^[1]

$t = \cos \,\zeta = \frac{1}{6} \left(\sqrt[3]{19 + 3\sqrt{33}} + \sqrt[3]{19 - 3\sqrt{33}} -2 \right)$

Sei d die Kantenlänge des abgeschrägten Hexaeders, so sind die resultierenden Seitenlängen des Tangentenfünfecks gegeben durch

$a = \frac{d}{2} \sqrt{2+2t}$

$b = \frac{d}{\sqrt{2+2t}}$

Hierbei sei mit a die längere der beiden Seiten bezeichnet.

Formeln

Nachstehend aufgeführte Formeln gelten für den Fall  $b = \frac{a}{1+t}$ bzw. äquivalent dazu $a = b\,(1+t)$

Für das Polyeder

Größen eines Pentagonikositetraeders mit Kantenlänge a und b
Volumen	$V = \frac{4a^3(2+3t)\sqrt{1-2t}}{(1+t)(1-4t^2)} = \frac{2b^3(1+t)(2+3t)}{(1-2t^2)\sqrt{1-2t}}$
Oberflächeninhalt	$O = \frac{24a^2(2+3t)}{1+2t} \sqrt{\frac{1-t}{1+t}} = \frac{12b^2(2+3t)}{(1-2t^2)} \sqrt{1-t^2}$
Kantenkugelradius	$r = \frac{a}{\sqrt{2\,(1+t)(1-2t)}} = b\,\sqrt{\frac{1+t}{2\,(1-2t)}}$
Inkugelradius	$\rho = \frac{a}{2\sqrt{(1-2t)(1-t^2)}} = \frac{b}{2}\, \sqrt{\frac{1+t}{(1-t)(1-2t)}}$
Flächenwinkel  ≈ 136,31°	$\cos \, \alpha= \frac{t}{t-1}$
3D-Kantenwinkel  ≈ 132,73°	$\cos \, \gamma = \frac{8t^4+2t^3-6t^2+1}{2t^3+2t^2-1}$

Für die Begrenzungsflächen

Größen des Tangentenfünfecks
Flächeninhalt	$A = \frac{a^2(2+3t)}{1+2t} \sqrt{\frac{1-t}{1+t}} = \frac{b^2(2+3t)}{2\,(1-2t^2)} \sqrt{1-t^2}$
Inkreisradius	$r = \frac{a}{2\sqrt{1-t^2}} = \frac{b}{2}\,\sqrt{\frac{1+t}{1-t}}$
Diagonale $\|\, b$	$e = 2a\,(1-2t^2) = b\,(1+2t)$
Stumpfe Winkel (4)  ≈ 114,81°	$\cos \, \alpha = -t$
Spitzer Winkel (1)  ≈ 80,75°	$\cos \, \beta = 1 - 2t$

Einzelnachweise

1. ↑ t ist die einzige reelle Lösung der kubischen Gleichung 4t³ + 4t² − 1 = 0. Wird zum doppelten Wert von t die Zahl 1 addiert, erhält man die Tribonacci-Konstante, welche den Limes des Verhältnisses (= 1,83928675521416…) zweier aufeinanderfolgenden Zahlen dieser Folge darstellt.

Weblinks

• Eric W. Weisstein: Pentagonikositetraeder. In: MathWorld. (englisch)

Platonische Körper

Tetraeder · Würfel · Oktaeder · Dodekaeder · Ikosaeder