Pentagonhexakontaeder

3D-Ansicht eines Pentagonhexakontaeders (Animation)

Netz des Pentagonhexakontaeders

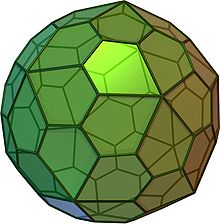
Das Pentagonhexakontaeder ist ein konvexes Polyeder, das sich aus 60 Fünfecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum abgeschrägten Dodekaeder und hat 92 Ecken sowie 150 Kanten.

Die folgenden Bilder zeigen zwei zueinander spiegelbildliche Pentagonhexakontaeder.

• 

  Spiegelvariante 1

• 

  Spiegelvariante 2

Entstehung

Konstruktion des Tangentenfünfecks am abgeschrägten Dodekaeder

Durch Verbinden der Mittelpunkte von jeweils fünf Kanten, die in jeder Raumecke des abgeschrägten Dodekaeders zusammenstoßen, entsteht ein Sehnenfünfeck, dessen Umkreis gleichzeitig Inkreis des Tangentenfünfecks, der Begrenzungsfläche des Pentagonhexakontaeders, ist. Bei diesem speziellen Typ sind alle Flächenwinkel gleich groß (≈ 153°), und es existiert ein einheitlicher Kantenkugelradius.

Nachfolgend bezeichne der Term t den Kosinus des kleineren Zentriwinkels ζ im zuvor erwähnten Sehnenfünfeck; φ sei die Goldene Zahl.

t ist die einzige reelle Lösung der kubischen Gleichung 8t³ + 8t² − φ² = 0.

$t = \cos \,\zeta = \frac{1}{12} \left(\sqrt[3]{44 + 12\varphi\,(9 + \sqrt{81\varphi-15})} + \sqrt[3]{44 + 12\varphi\,(9 - \sqrt{81\varphi-15})} -4 \right)$ ^[1]

Sei d die Kantenlänge des abgeschrägten Dodekaeders, so sind die resultierenden Seitenlängen des Tangentenfünfecks gegeben durch

$a = \frac{d\,(1+2t)}{2\,(1-2t^2)\sqrt{2+2t}}$

$b = \frac{d}{\sqrt{2+2t}}$.

Hierbei sei mit a die längere der beiden Seiten bezeichnet.

Formeln

Nachstehend aufgeführte Formeln gelten für den Fall, dass $b = \frac{2a\,(1-2t^2)}{1+2t}$ bzw. äquivalent dazu $a = \frac{b\,(1+2t)}{2\,(1-2t^2)}$ ist.^[2]

Für das Polyeder

Größen eines Pentagonhexakontaeders mit Kantenlänge a und b
Volumen	$V = \frac{40a^3(1+t)(2+3t)(1-2t^2)^2}{(1+2t)^3\sqrt{1-2t}} = \frac{5b^3(1+t)(2+3t)}{(1-2t^2)\sqrt{1-2t}}$
Oberflächeninhalt	$O = \frac{120a^2(2+3t)(1-2t^2)}{(1+2t)^2} \sqrt{1-t^2} = \frac{30b^2(2+3t)}{(1-2t^2)} \sqrt{1-t^2}$
Kantenkugelradius	$r = \frac{a\,(1-2t^2)}{1-4t^2} \sqrt{2\,(1+t)(1-2t)} = b\,\sqrt{\frac{1+t}{2\,(1-2t)}}$
Inkugelradius	$\rho = \frac{a\,(1-2t^2)}{1+2t} \sqrt{\frac{1+t}{(1-t)(1-2t)}} = \frac{b}{2}\, \sqrt{\frac{1+t}{(1-t)(1-2t)}}$
Flächenwinkel  ≈ 153,18°	$\cos \, \alpha= \frac{t}{t-1}$

Für die Begrenzungsflächen

Größen des Tangentenfünfecks
Flächeninhalt	$A = \frac{2a^2(2+3t)(1-2t^2)}{(1+2t)^2} \sqrt{1-t^2} = \frac{b^2(2+3t)}{2\,(1-2t^2)} \sqrt{1-t^2}$
Inkreisradius	$r = \frac{a\,(1-2t^2)}{1+2t}\sqrt{\frac{1+t}{1-t}} = \frac{b}{2}\,\sqrt{\frac{1+t}{1-t}}$
Diagonale $\|\, b$	$e = 2a\,(1-2t^2) = b\,(1+2t)$
Stumpfe Winkel (4)  ≈ 118,14°	$\cos \, \alpha = -t$
Spitzer Winkel (1)  ≈ 67,45°	$\cos \, \beta = 1 - 2\,(1-2t^2)^2$

Anwendung

In den USA ist ein Verfahren patentiert, bei dem 92 der insgesamt 332 Vertiefungen („dimples“) eines Golfballs auf den Gitterpunkten eines Pentagonhexakontaeders liegen.^[3]

Einzelnachweise

1. ↑ t ≈ 0,47157563
2. ↑ Diese Formeln haben auch Gültigkeit für das Pentagonikositetraeder sowie das Pentagondodekaeder (mit jew. n Flächen), wenn man die entsprechenden Werte für t (Kosinus des kleineren Zentriwinkels) einsetzt und ferner beachtet, dass O = n·A und V = 1/3·O·ρ ist.
3. ↑ Pentagonal hexecontahedron dimple pattern on golf balls (engl.)

Weblinks

• Eric W. Weisstein: Pentagonhexakontaeder. In: MathWorld. (englisch)

Platonische Körper

Tetraeder · Würfel · Oktaeder · Dodekaeder · Ikosaeder