- Zopfgruppe
-
Die Zopfgruppe Bn ist die Gruppe, deren Elemente n-strängige Zöpfe sind. Die Gruppenoperation ist die Aneinanderhängung von Zöpfen und das neutrale Element ist der n-Zopf ohne Überkreuzungen. Es gibt für jede natürliche Zahl n eine Zopfgruppe Bn. Zopfgruppen werden in dem mathematischen Gebiet der Topologie untersucht. Zopfgruppen wurden erstmalig in dem Artikel Theorie der Zöpfe aus dem Jahr 1925 von Emil Artin definiert; eine ähnliche Konstruktion gab es aber auch schon 1891 in einer Arbeit von Adolf Hurwitz.[1]
Inhaltsverzeichnis
Geometrische Definition
Ein n-strängiger Zopf ist eine Menge von n sich nicht schneidenden Kurven ki (mit
 ) in
) in  , die in
, die in  beginnen, in
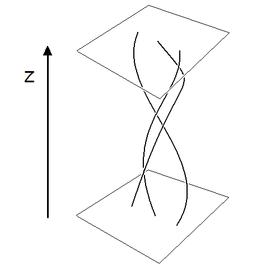
beginnen, in  enden und in deren Parametrisierung die dritte Koordinatenfunktion (in der Abbildung die z-Koordinate) monoton steigend ist. Diese Kurven werden Stränge genannt.
enden und in deren Parametrisierung die dritte Koordinatenfunktion (in der Abbildung die z-Koordinate) monoton steigend ist. Diese Kurven werden Stränge genannt.Jedem n-Zopf ordnet man folgendermaßen ein Element σ der symmetrischen Gruppe Sn zu: die Permutation σ ist dadurch definiert, dass man dem i-ten Strang zu seinem Endpunkt σ(i) folgt. Der Kern dieser Abbildung ist die sogenannte reine Zopfgruppe. Sie besteht also nur aus solchen Zöpfen, bei denen der i-te Strang an Position i endet.
Zwei Zöpfe b0 und b1 sind äquivalent, wenn sie isotop sind, das heißt, wenn eine stetige Familie von Zöpfen
 existiert, die in b0 startet und b1 endet.
existiert, die in b0 startet und b1 endet.Gruppeneigenschaften
Die Menge aller (Äquivalenzklassen von) n-strängigen Zöpfe erzeugt eine Gruppe. Die Verknüpfung ist das Anfügen eines Zopfes unter dem anderen, wobei die z-Koordinate reskaliert wird. Das Einselement der Gruppe ist der Zopf mit n parallelen Strängen. Das inverse Element eines Zopfes ist gerade dessen Spiegelung.
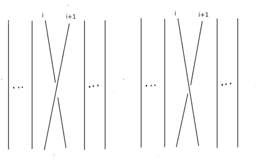
Man kann jeden Zopf als eine Folge von Über- bzw. Unterkreuzungen der Stränge darstellen. Das sind gerade die in der Abbildung gezeigten Erzeuger
 bzw.
bzw.  .
.Man kann sich in einer Skizze veranschaulichen, dass jeder Erzeuger
 multipliziert mit seinem Inversen
multipliziert mit seinem Inversen  das neutrale Element ergibt.
das neutrale Element ergibt.Darstellung durch Erzeuger und Relationen
Die Zopfgruppe Bn besitzt die folgende Darstellung durch Erzeuger und Relationen:
Erzeuger:
 .
.
Relationen:
 für
für 
 für
für 
Diese algebraische Definition ist mit der geometrischen äquivalent.
Beispiele
Die Zopfgruppe B1 besteht nur aus einem Element. Die Zopfgruppe B2 ist die unendliche zyklische Gruppe
 . Die Zopfgruppe B3 hat die Darstellung
. Die Zopfgruppe B3 hat die Darstellungund ist nicht-kommutativ.
Anwendungen
Mathematiker interessiert vor allem die Anwendung in der Knotentheorie: Indem man das obere Ende des Zopfes mit dem unteren Ende verbindet, erhält man eine Verschlingung. Äquivalente Zöpfe erzeugen äquivalente Verschlingungen. Andererseits kann jede Verschlingung durch isotope Umformung in die Form eines geschlossenen Zopfes gebracht werden (Satz von Alexander). Wann zwei Zöpfe dieselbe Verschlingung erzeugen, klärt der Satz von Markov (Andrei Andrejewitsch Markov, 1903 - 1979, Sohn von Andrei Andrejewitsch Markow, 1856 - 1922).
Literatur
- Emil Artin: Theorie der Zöpfe. In: Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg. 4, 1925, ISSN 0025-5858, S. 47–72.
- Joan S. Birman: Braids, Links, and Mapping Class Groups. Based on Lecture Notes by James Cannon. Princeton University Press, Princeton NJ 1975, ISBN 0-691-08149-2 (Annals of Mathematics Studies 82).
- Moritz Epple: Die Entstehung der Knotentheorie. Kontexte und Konstruktionen einer modernen mathematischen Theorie. Vieweg, Braunschweig u. a. 1999, ISBN 3-528-06787-X.
- Christian Kassel, Vladimir Turaev: Braid Groups. Springer, New York NY 2008, ISBN 978-0-387-33841-5 (Graduate Texts in Mathematics 247).
- Bohdan I. Kurpita, Kunio Murasugi: A Study of Braids. Kluwer, Dordrecht u. a. 1999, ISBN 0-7923-5767-1 (Mathematics and its Applications 484).
- Vassily Manturov: Knot Theory. Routledge Chapman & Hall, Boca Raton FL u. a. 2004, ISBN 0-415-31001-6 (online bei GoogleBooks).
Quellen
- ↑ Siehe hierzu das Buch von Epple.
Wikimedia Foundation.