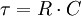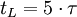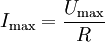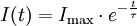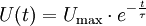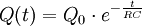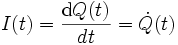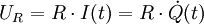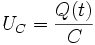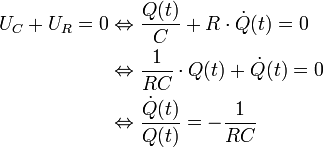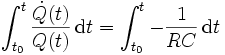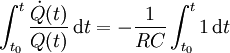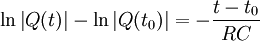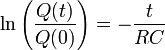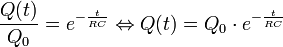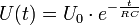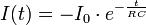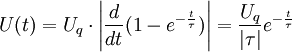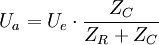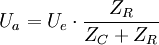Differenzierglied

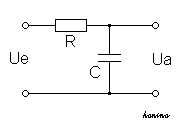
Unter RC-Gliedern versteht man in der Elektronik Schaltungen, die aus einem ohmschen Widerstand (R - engl. resistor) und einem Kondensator (C - engl. capacitor) aufgebaut sind. Es ist ein lineares, zeitinvariantes System. In erster Linie sind damit die Frequenzfilter Tiefpass und Hochpass gemeint (wobei letzteres systematisch CR-Glied genannt werden könnte).

Einfacher RC-Tiefpass

Verhalten im Zeitbereich

Ladevorgang

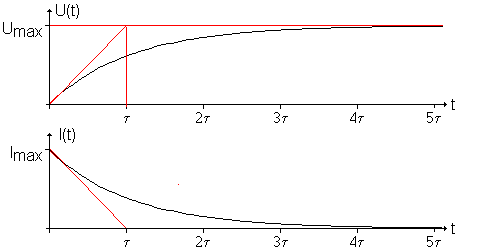
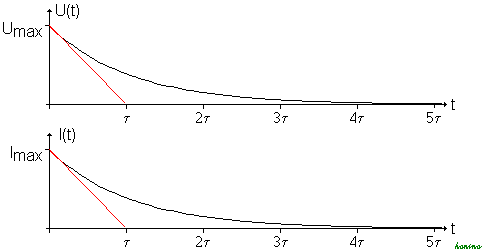
Exemplarisch ist hier die Systemantwort auf eine Sprungfunktion dargestellt. Die Spannung beträgt null Volt bis zum Zeitpunkt null und steigt dann unmittelbar auf U_max.
In den Kondensator fließt so lange Strom, bis die Platten elektrisch aufgeladen sind und keine weitere Ladung annehmen. Das tritt auf, wenn die Kondensatorspannung U(t) genauso groß wie die angelegte Spannung U_max ist. Die eine Platte ist dann elektrisch positiv, die andere negativ geladen. Auf der negativ geladenen Seite herrscht ein Elektronenüberschuss.

Die Ladezeit des Kondensators ist proportional zur Größe des Widerstands R und zur Kapazität C des Kondensators. Das Produkt von Widerstand und Kapazität nennt man die Zeitkonstante τ.

$\tau = R \cdot C \,$

Theoretisch dauert es unendlich lange, bis U(t)=U_max ist. Für praktische Zwecke kann man als Ladezeit t_L verwenden, nach der der Kondensator näherungsweise als vollständig (mehr als 99%) geladen angesehen werden kann.

$t_{L} = 5 \cdot \tau \,$

Verlauf von Spannung U und Strom I beim Ladevorgang,
U_max ist die Spannung der Spannungsquelle als maximal mögliche Spannung

Die Zeitkonstante τ markiert zugleich den Zeitpunkt, an dem die am Beginn der Kurve angelegte Tangente den Endwert der Spannung erreicht. Nach dieser Zeit wäre der Kondensator auf den Endwert geladen, wenn man ihn mit dem konstanten Strom I_max laden könnte. Tatsächlich nimmt die Stromstärke bei konstanter angelegter Spannung jedoch mit der Zeit exponentiell ab.

Der maximale Strom I_max fließt zum Zeitpunkt t=0. Dieser ergibt sich durch den Widerstand R nach dem ohmschen Gesetz, wobei U_max die angelegte Spannung der Spannungsquelle ist:

$I_{\rm max} = \frac{U_{\rm max}}{R} \,$

Der Verlauf der Ladespannung U(t) bzw. deren jeweilige zeitliche Größe wird mit der folgenden Gleichung beschrieben, wobei e die eulersche Zahl, t die Zeit nach Beginn der Ladung und τ die Zeitkonstante sind:

$U(t) = U_{\rm max} \cdot (1 - e^{-\frac{t}{\tau}}) \,$,

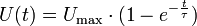Dabei wird vorausgesetzt, dass der Kondensator zu Beginn ungeladen war: U(t = 0) = 0. Die Spannung ist also im ersten Moment null und steigt dann in Form einer Exponentialfunktion an. Nach der Zeit t = τ hat die Spannung etwa 63% der angelegten Spannung U_max erreicht. Nach der Zeit t = 5τ ist der Kondensator auf mehr als 99% aufgeladen.

Der Verlauf der Stromstärke I(t) bzw. deren jeweilige zeitliche Größe wird mit der folgenden Gleichung beschrieben:

$I(t) = I_{\rm max} \cdot e^{-\frac{t}{\tau}} \,$

Hier beträgt der Strom im ersten Moment I(t = 0) = I_max und nimmt dann in Form einer Exponentialfunktion wie beim Entladevorgang ab. Nach der Zeit t = τ beträgt der Strom nur noch etwa 37% seines Anfangswertes und nach der Zeit t = 5τ ist er auf weniger als 1% abgefallen.

Entladevorgang

Das Bild zeigt den Entladevorgang, wenn der Kondensator zu Beginn auf den Wert U_max geladen ist und über den Widerstand R entladen wird. Hier sind sowohl die Spannung als auch die Stromstärke zu Beginn am größten:

Für t = 0 gilt: 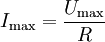$I_{\rm max} = \frac{U_{\rm max}}{R}$      und beträgt zu einem beliebigen Zeitpunkt danach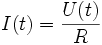      $I(t) = \frac{U(t)}{R}$

Verlauf von Spannung U und Strom I beim Entladevorgang,
U_max ist die Anfangsspannung

Die Spannung nimmt im Verlauf der Entladung mit der Zeit ab gemäß

$U(t) = U_{\rm max} \cdot e^{-\frac{t}{\tau}} \,$

Der Strom, der mit der Spannung U(t) über den Entladewiderstand R verknüpft ist, zeigt den entsprechenden Verlauf

$I(t) = I_{\rm max} \cdot e^{-\frac{t}{\tau}} \,$

Der Entladestrom ist bei der vorgegebenen Zählpfeilrichtung negativ.

Differentialgleichung der Entladung

Für den Entladevorgang des Kondensators gilt:

$Q(t) = Q_0 \cdot e^{- \frac{t}{RC}}$

Diese leitet sich wie folgt her. Für die Stromstärke gilt:

$I(t)= \frac{\mathrm dQ(t)}{dt} = \dot Q(t)$

Für die Spannung am ohmschen Widerstand gilt:

$U_R = R \cdot I(t) = R \cdot \dot Q(t)$

Für die Spannung am Kondensator gilt:

$U_C = \frac{Q(t)}{C}$

Für eine einfache Schaltung aus Kondensator und Ohmschem Widerstand gilt gemäß Maschensatz:

$\begin{align} U_C + U_R = 0 & \Leftrightarrow \frac{Q(t)}{C} + R \cdot \dot Q(t) = 0 \\ & \Leftrightarrow \frac{1}{RC} \cdot Q(t) + \dot Q(t) = 0 \\ & \Leftrightarrow \frac{\dot Q(t)}{Q(t)} = - \frac{1}{RC} \end{align}$

Diese Differentialgleichung ist nun zu lösen. Das geschieht durch Integration:

$\int_{t_0}^t \frac{\dot Q(t)}{Q(t)}\,\mathrm dt = \int_{t_0}^t -\frac{1}{RC}\,\mathrm \mathrm dt$

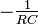Da $- \tfrac{1}{RC}$ konstant ist, gilt:

$\int_{t_0}^t \frac{\dot Q(t)}{Q(t)}\,\mathrm dt = -\frac{1}{RC} \int_{t_0}^t 1\,\mathrm dt$

Nach der Substitutionsregel gilt:

$\ln\left|Q(t)\right| - \ln\left|Q(t_0)\right| = - \frac {t-t_0}{RC}$

Q(t) ist die elektrische Ladung des Kondensators zum Zeitpunkt t, sie kann nicht negativ werden, t₀ ist der Zeitpunkt zu Beginn der Entladung und hat den Wert 0 s; es folgt:

$\ln \left( \frac{Q(t)}{Q(0)}\right) = - \frac{t}{RC}$

Durch Potenzieren zur Basis e erhält man:

$\frac{Q(t)}{Q_0} = e^{- \frac{t}{RC}} \Leftrightarrow Q(t) = Q_0 \cdot e^{- \frac{t}{RC}}$

Analog dazu gilt für die Spannung U:

$U(t) = U_0 \cdot e^{- \frac{t}{RC}}$

und für die Stromstärke I:

$I(t) = -I_0 \cdot e^{- \frac{t}{RC}}$

Impulsantwort

Die Impulsantwort beschreibt den Ausgangsspannungsverlauf auf eine diracimpulsförmige Eingangsspannung, der Ableitung der Sprungfunktion. Da das RC-Glied ein lineares System ist, ist auch der Ausgangsspannungsverlauf durch die Ableitung vorgegeben:

$U(t) = U_q \cdot \left|\frac{d}{dt}(1 - e^{-\frac{t}{\tau}})\right| = \frac{U_q}{|\tau |}e^{-\frac{t}{\tau}} \,$

Periodische Signale

Die Filterwirkung wird insbesondere bei Rechtecksignalen deutlich; die Filterantwort setzt sich aus Segmenten des Lade- und Entladeverhaltens zusammen:

Verhalten im Frequenzbereich

Tiefpass

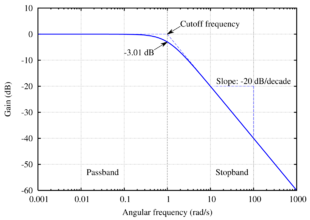Amplitudengang eines RC-Tiefpassfilters. Die Ordinate zeigt die Amplitudenverhältnis | H | in Dezibel, die Abszisse die normierte Kreisfrequenz Ω in logarithmischer Darstellung.

Phasenverschiebung als Funktion der Frequenz am RC-Glied

Phasenverschiebung von 90° zwischen Strom und Spannung am Kondensator

Widerstand und Kondensator bilden einen frequenzabhängigen Spannungsteiler, der auch eine Phasenverschiebung von maximal 90° bewirkt. Die Impedanzen Z sind R bzw. 1 / (jωC). Für das RC-Glied gilt für eine harmonisch oszillierende Spannung der Frequenz $f = \frac{\omega}{2\pi}$:

$U_a = U_e \cdot \frac{Z_C}{Z_R+Z_C} \,$

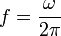und somit für das Übertragungsverhalten, das als Quotienten von Ausgangs- zur Eingangsspannung definiert ist:

$H=\frac{U_a}{U_e}=\frac{Z_C}{Z_R+Z_C}=\frac{\frac{1}{j\omega C}}{R+\frac{1}{j\omega C}}= \frac{1}{1+j\omega RC}=\frac{1}{1+j\Omega} \,$,

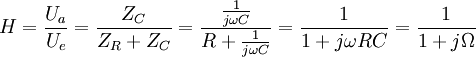wobei die normierte Frequenz Ω = ω/ω₀ sich aus der Division von Kreisfrequenz ω = 2πf und Grenzfrequenz (Übergangsfrequenz, Eckfrequenz oder englisch cutoff frequency) ω₀ = 1/(RC) = 1/τ ergibt.

Für tiefe Frequenzen Ω << 1 ist H ungefähr 1, Ein- und Ausgangsspannung etwa gleich, weshalb man den Bereich auch engl. als Passband bezeichnet.
Für Frequenzen Ω >> 1 fällt H mit 20 dB pro Dekade = 6 dB pro Oktave ab. Der weggefilterte Bereich wird englisch mit Stopband bezeichnet.

Bei sehr tiefen Frequenzen, die deutlich kleiner als die Grenzfrequenz sind, fällt der Ladestrom des Kondensators nicht ins Gewicht und Eingangs- und Ausgangsspannung unterscheiden sich nur unmerklich. Die Phasenverschiebung beträgt 0°.

Steigt die Frequenz, dauert es - im Vergleich zur Schwingungsdauer - immer länger, bis der Kondensator auf die Eingangsspannung aufgeladen ist. Deshalb steigt die Phasenverschiebung.

Bei sehr hoher Frequenz strebt diese dem Grenzwert von 90° zu, allerdings wird dann die Spannung am Kondensator auch unmessbar klein.

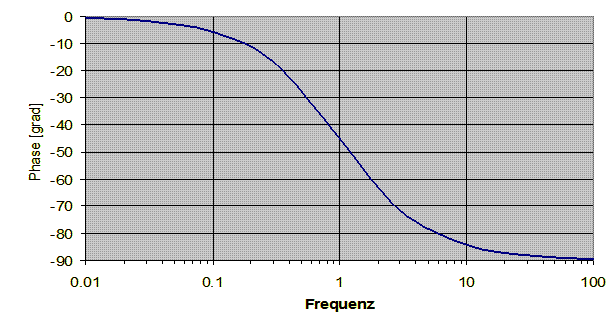
Hochpass

Die Verschaltung als Hochpass unterscheidet sich von der des Tiefpasses durch Vertauschung von R und C. Demgemäß gilt

$U_a = U_e \cdot \frac{Z_R}{Z_C+Z_R} \,$

und

$H=\frac{U_a}{U_e}=\frac{Z_R}{Z_C+Z_R}=\frac{R}{\frac{1}{j\omega C}+R}= \frac{j\omega RC}{1+j\omega RC}=\frac{j\Omega}{1+j\Omega} \,$,

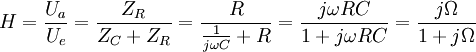Der Amplitudengang ist gegenüber dem Tiefpass entlang Ω = 1 gespiegelt, hohe Frequenzen können nahezu ungedämpft passieren.

Beschreibung im Spektralbereich (Laplace-Transformation)

Mit einer analogen Herleitung erhält man für den Tiefpass

$H(s)=\frac{1}{1+sRC} \,$,

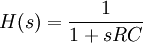eine Polstelle bei s = − 1 / RC.

Bei dem Hochpass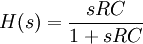

$H(s)=\frac{sRC}{1+sRC} \,$,

ergibt sich ebenfalls eine Polstelle bei s = − 1 / RC, zusätzlich eine Nullstelle im Ursprung.

Weblinks

• RC-Glied Berechnung Übergangsfrequenz und Zeitkonstante