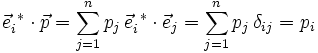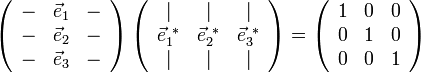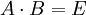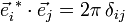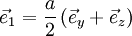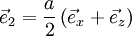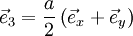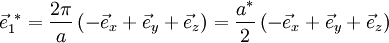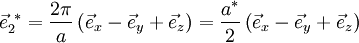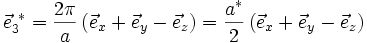- Affines Koordinatensystem
-
Dieser Artikel wurde auf der Qualitätssicherungsseite des Portals Mathematik eingetragen. Dies geschieht, um die Qualität der Artikel aus dem Themengebiet Mathematik auf ein akzeptables Niveau zu bringen. Dabei werden Artikel gelöscht, die nicht signifikant verbessert werden können. Bitte hilf mit, die Mängel dieses Artikels zu beseitigen, und beteilige dich bitte an der Diskussion!
Man spricht von affinen Koordinaten oder geradlinigen Koordinaten, wenn die Koordinatenlinien durch Geraden gebildet werden. Affine Koordinaten können sowohl schiefwinklig als auch orthogonal (senkrecht) sein. Im letzteren Fall spricht man von kartesischen Koordinaten.
Abzugrenzen sind die geradlinigen Koordinaten von krummlinigen Koordinaten. Die Basisvektoren krummliniger Koordinaten sind im Allgemeinen vom Ort abhängig.
Inhaltsverzeichnis
Definition
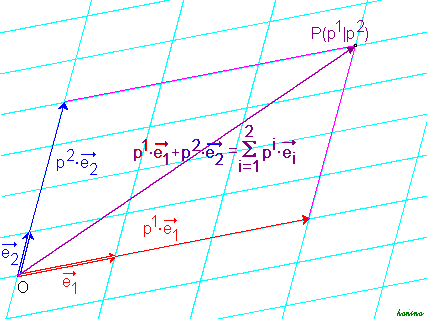
Affine Koordinaten eines Vektors
Ein beliebiger Vektor
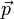 in einem n-dimensionalen Vektorraum lässt sich durch eine Linearkombination
in einem n-dimensionalen Vektorraum lässt sich durch eine Linearkombination 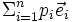 linear unabhängiger Vektoren
linear unabhängiger Vektoren 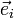 darstellen. Die Skalare pi sind die affinen Koordinaten des Vektors
darstellen. Die Skalare pi sind die affinen Koordinaten des Vektors 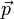 bzgl.
bzgl. 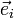 .
.Affine Koordinaten eines Punktes
Die affinen Koordinaten eines Punktes P erhält man nach Festlegung eines Ursprungs O als die affinen Koordinaten des zugehörigen Ortsvektors
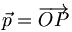 .
.Schiefwinklige affine Koordinaten
Bei schiefwinkligen affinen Koordinaten ist das Skalarprodukt zwischen verschiedenen Einheitsvektoren
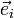 ungleich Null:
ungleich Null: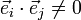 für
für 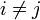
Um die Vektorkomponente pi eines gegebenen Vektors
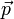 zu erhalten verwendet man die Vektoren der dualen Basis
zu erhalten verwendet man die Vektoren der dualen Basis 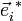 . Diese erfüllen die Relation:
. Diese erfüllen die Relation:Mittels Projektion erhält man die Vektorkomponente pi:
Duale Basis
Zur Berechnung der dualen Basis für endlich-dimensionale Vektorräume: Die Beziehung
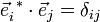 lässt sich auch als Matrix-Gleichung auffassen. Schreibe die kartesichen Koordinaten der Basisvektoren als Zeilen in die erste Matrix; die Spalten der zweiten Matrix sollen die kartesischen Komponenten der gesuchten dualen Basisvektoren enthalten (hier exemplarisch für 3-dimensionalen Vektorraum):
lässt sich auch als Matrix-Gleichung auffassen. Schreibe die kartesichen Koordinaten der Basisvektoren als Zeilen in die erste Matrix; die Spalten der zweiten Matrix sollen die kartesischen Komponenten der gesuchten dualen Basisvektoren enthalten (hier exemplarisch für 3-dimensionalen Vektorraum):Bezeichne die erste Matrix mit A und die zweite mit B, die Einheitsmatrix mit E, so schreibt sich das lineare Gleichungssystem:
Dessen Lösung ist die inverse Matrix von A:
- B = A − 1
Die dualen Basisvektoren lassen sich nun als Spalten der Matrix B ablesen.
Für orthogonale Koordinaten stimmen Basisvektoren und duale Basisvektoren bis auf eine Konstante überein:
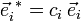 . Dabei ist
. Dabei ist 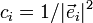 . Sind die orthogonalen Basisvektoren normiert, so sind die ci = 1 und somit Basis und duale Basis identisch.
. Sind die orthogonalen Basisvektoren normiert, so sind die ci = 1 und somit Basis und duale Basis identisch.Anwendung
Affine Koordinaten sind wichtig bei der Beschreibung von Kristallgittern. Dort sind die primitiven Gittervektoren im Allgemeinen schiefwinklig. Das Skalarprodukt zwischen Basisvektoren des reziproken Raums
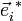 (entspricht dualem Raum bis auf konstanten Faktor 2π) und des Ortsraums
(entspricht dualem Raum bis auf konstanten Faktor 2π) und des Ortsraums 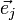 ist hier:
ist hier:Beispiel: Die primitiven Gittervektoren des kubisch-flächenzentrierten (fcc) Gitters lauten:
Die Matrix A zeilenweise mit den kartesischen Koordinaten der Basisvektoren auffüllen, dann invertieren und schließlich mit 2π multiplizieren:
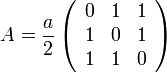 mit
mit 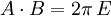 ergibt sich
ergibt sich 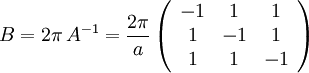
Die reziproke Basisvektoren lassen sich als Spalten der Matrix B einfach ablesen:
Diese bilden ein kubisch-raumzentriertes (bcc) Gitter mit der Gitterkonstanten
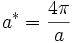 .
.
Wikimedia Foundation.