- Feld (Physik)
-
Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.
Ein Feld bezeichnet in der Physik eine für alle Punkte
 des Raums
des Raums  definierte sogen. Ortsfunktion
definierte sogen. Ortsfunktion  , die jedem Punkt im Raum einen Funktionswert
, die jedem Punkt im Raum einen Funktionswert  , z.B. eine Dichte, Temperatur, Kraft o.ä. zuordnet, wobei diese Funktionswerte vom Prinzip her beliebiger Natur sein können.
, z.B. eine Dichte, Temperatur, Kraft o.ä. zuordnet, wobei diese Funktionswerte vom Prinzip her beliebiger Natur sein können.In der Praxis am häufigsten sind es dabei einfach nur reelle Zahlen (sogen. Skalare), aber auch gerichtete Größen wie Vektoren oder (in relativistischen Zusammenhängen) Vierervektoren, die meist außerdem mit einer physikalischen Einheit versehen sind und oft auch eine unmittelbar anschauliche physikalische Bedeutung besitzen. Physikalische Felder können eine eigene Dynamik entwickeln, die durch entsprechende Feldgleichungen beschrieben wird.
Felder sind dem eingangs Gesagten gemäß vom Prinzip her stets unendlich weit ausgedehnt - wenn dennoch in praktischen Zusammenhängen von der „Reichweite“ eines Feldes die Rede ist, sind damit in der Regel die Grenzen seiner Nachweisbarkeit gemeint, die wiederum von der Empfindlichkeit der verwendeten Messapparatur abhängen. Möglich ist aber auch der Ausschluss bestimmter einzelner Punkte oder ganzer Areale des Raums vom Definitionsbereich des Feldes, etwa beim Gravitationsfeld, das für den Koordinatenursprung selbst undefiniert ist.
Inhaltsverzeichnis
Beispiele und Einteilung der Felder
Der Feldbegriff findet in allen Zweigen der Physik Anwendung, wobei man die einzelnen Felder noch einmal nach verschiedenen Kriterien ordnen kann:
- Nach der physikalischen Natur ihres Funktionswerts:
- Nach der mathematischen Natur ihres Funktionswerts:
- Skalarfelder haben Skalare als Funktionswerte bzw. Feldgrößen, etwa die Massedichte oder die Temperatur. Ein wichtiges Skalarfeld ist das physikalische Potential.
- Vektorfelder haben Vektoren als Funktionswerte bzw. Feldgrößen, etwa die Kraft oder die elektrische Feldstärke.
- Tensorfelder haben Tensoren als Funktionswerte bzw. Feldgrößen, etwa die elastische Spannung.
- Spinorfelder haben Spinoren als Funktionswerte bzw. Feldgrößen, etwa die Stromdichte in relativistischer Feldbeschreibung (Dirac-Feld), wobei auch Felder mit Spinoren höherer Ordnung beschreibbar sind.
- Nach ihrer zeitlichen (Un)Veränderlichkeit:
- Statische Felder besitzen Funktionswerte bzw. Feldgrößen, die zeitunabhängig sind, und damit beispielsweise Gegenstand der Elektrostatik, Magnetostatik, Hydrostatik, Aerostatik oder einfach nur der Statik als solcher.
- Stationäre Felder besitzen Funktionswerte bzw. Feldgrößen, die zwar nicht zeitunabhängig sind, sich aber gleichwohl nicht mit der Zeit ändern, zum Beispiel ein Magnetfeld um einen ruhenden, von einem konstanten Gleichstrom durchflossenen unveränderlichen Leiter, oder eine stationäre Strömung einer Flüssigkeit bzw. eines als inkompressibel (nicht komprimierbar) betrachteten Gases.
- Quasistationär schließlich nennt man Felder, deren Funktionswerte bzw. Feldgrößen sich zwar mit der Zeit ändern, doch nur so wenig, dass diese Veränderung für die aktuelle Betrachtung praktisch vernachlässigbar ist.
Motivation des Begriffs
Die Motivation zur Einführung des Feldbegriffs liegt
- einerseits in der einfacheren Beschreibung physikalischer Vorgänge in Vielteilchensystemen. Statt alle Orte und Geschwindigkeiten der Einzelteilchen angeben zu müssen, ermöglicht die Feldbeschreibung eine elegante Methode, Temperatur und Dichte eines Gases oder einer Flüssigkeit zu behandeln.
- andererseits in der Beachtung der Nahwirkung, die wegen der endlichen Übertragungsgeschwindigkeit physikalischer Ereignisse und Wechselwirkungen in Betracht gezogen werden muss. Das Feld besteht dann aus nicht weiter reduzierbaren physikalischen Größen, wie im elektromagnetischen Feld und im Gravitationsfeld.
Anwendung
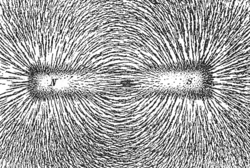
Im praktischen Umfeld finden die Vektorfelder die größte Verbreitung. Sie können besonders anschaulich mit Hilfe von Feldlinien beschrieben werden, deren Tangenten in jedem Raumpunkt die Richtung der Feldgrößen (Vektoren) darstellen. Die Feldstärke, also der Betrag der Feldvektoren in den Raumpunkten, wird durch die Dichte der Feldlinien dargestellt. Solche Feldlinien können in Experimenten verdeutlicht werden, man denke an das magnetische Feld, das mittels Eisenfeilspänen dargestellt werden kann.
Feldlinien können von bestimmten Punkten im Raum ausgehen und in anderen Punkten verschwinden (Quelle und Senke) – Felder dieser Art heißen ganz allgemein Quellenfelder. Beispiel hierfür sind das elektrostatische Feld einer positiven und negativen elektrischen Ladung oder das Gravitationsfeld.
Bei anderen Feldern dagegen können die Feldlinien nur als in sich geschlossene Endlosschleifen auftreten – Felder dieser Art heißen ganz allgemein Wirbelfelder. Bekanntestes Beispiel hierfür ist das Magnetfeld.
Literatur
- Hartmann Römer, Michael Forger: Elementare Feldtheorie: Elektrodynamik, Hydrodynamik, spezielle Relativitätstheorie. VCH, Weinheim 1993, ISBN 3-527-29065-6.
Einzelnachweise
Wikimedia Foundation.