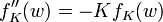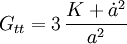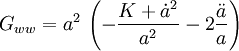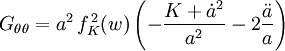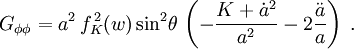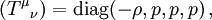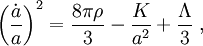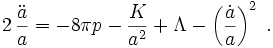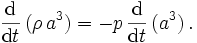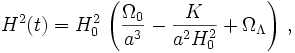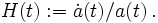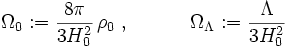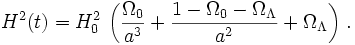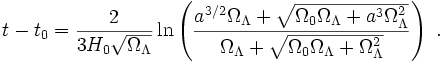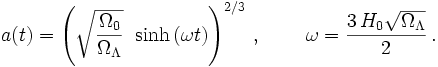- Friedmangleichung
-
Die Friedmann-Gleichungen beschreiben theoretisch die Entwicklung des Universums. Konkreter machen sie je nach Energiegehalt des Universums Voraussagen über dessen Expansion oder Kontraktion. Man erhält die Gleichungen durch Anwendung des Kosmologischen Prinzips („das Universum ist räumlich homogen und isotrop“) in der allgemeinen Relativitätstheorie.
Die Gleichungen lauten:
Hierbei bezeichnet ρ die totale Energiedichte (inklusive der kosmologischen Konstanten), p den Druck, a den Skalenfaktor, G die Gravitationskonstante, K den Krümmungsparameter und H den Hubble-Skalar.
Inhaltsverzeichnis
Grundlegendes
Albert Einstein ging zunächst von einem statischen Universum aus, das sich weder ausdehnt noch zusammenzieht. Dazu musste er in seinen Gleichungen der allgemeinen Relativitätstheorie eine entsprechende Konstante einführen, die er kosmologische Konstante (Λ) nannte.
Der russische Mathematiker und Physiker Alexander Friedmann verwarf diese Annahme eines statischen Universums und setzte die kosmologische Konstante gleich Null. Stattdessen stellte er mit den nach ihm benannten Friedmann-Gleichungen drei Modelle eines expandierenden Universums auf. Diese beeinflussten in der Folge erheblich die physikalischen Auffassungen und Modelle Einsteins.
Die Gleichungen sagen in Abhängigkeit von der totalen Energiedichte verschiedene Werte für die Krümmung der Raumzeit voraus (entsprechend den Werten -1, 0 oder 1 für K in obigen Gleichungen):
- 1. Modell: Die Energiedichte des Universums ist größer als die kritische Energiedichte (siehe unten). Dann ist die Krümmung der Raumzeit positiv (K = 1), das Universum „sphärisch“ (ein zweidimensionales Analogon wäre die Oberfläche einer Kugel). Ein solches sphärisches Universum ist übrigens auch geschlossen: Obwohl unbegrenzt wäre es nur endlich groß. Wer lange genug in eine Richtung läuft, kommt irgendwann zu seinem Ausgangspunkt zurück.
- 2. Modell: Die Energiedichte ist genau so groß wie die kritische Energiedichte. Die Raumzeit hat verschwindende Krümmung (K = 0), das Universum ist „flach“ (entsprechend einer Ebene in zwei Dimensionen).
- 3. Modell: Die Energiedichte ist kleiner als der kritische Wert. Die Krümmung der Raumzeit ist negativ (K = − 1), das Universum „hyperbolisch“ (eine solche Raumzeit lässt sich nicht in zwei Dimensionen visualisieren).
Je nach Zustandsgleichung der im Universum enthaltenen Materie ergeben sich auch drei verschiedene Möglichkeiten für die weitere Entwicklung des Universums:
- 1. Möglichkeit: Die Gravitation ist in der Lage, die Expansion soweit abzubremsen, dass sie zum Stillstand kommt und sich umkehrt. Das Universum zieht sich auf einen einzigen Punkt zusammen (Big Crunch). Über die weitere Entwicklung „nach“ diesem Ereignis kann nur spekuliert werden. Einige Szenarien sehen die Möglichkeit eines „pulsierenden“ Universums vor.
- 2. Möglichkeit: Die Gravitation verlangsamt die Expansion immer weiter, bringt sie jedoch nicht zum Stillstand.
- 3. Möglichkeit: Die Expansion beschleunigt sich und die gewöhnliche Materie im Universum wird immer weiter ausgedünnt.
Die verschiedenen Möglichkeiten für die Krümmung und das Expansionsverhalten des Universums sind zunächst unabhängig von einander. Erst durch verschiedene einschränkende Annahmen über die vorkommenden Materieformen ergeben sich Abhängigkeiten.
Die Expansion des Universums wurde 1929 von Edwin Hubble durch astronomische Beobachtungen entdeckt. Diese Beobachtungen bestätigten damit Friedmanns Grundannahme eines expandierenden Universums.
Die Expansionsrate wird mit der Hubble-Konstante H0 angegeben. Aus H0 lässt sich das Alter des Universums bestimmen, wobei jedes der drei Modelle einen anderen Wert liefert.
Aus neuesten Messungen der Expansionsrate über die Hintergrundstrahlung des Weltalls ergibt sich derzeit (März 2004) folgendes Bild:
- Die Hubble-Konstante beträgt 71 km/(s * Megaparsec), wobei gilt: 1 Parsec = 3,26 Lichtjahre. Daraus ergibt sich ein Alter des Universums von 13,7 Milliarden Jahren.
- Das Universum ist im Rahmen der Messgenauigkeit flach.
- Die Expansion beschleunigt sich.
Die gesamte Energiedichte des Universums setzt sich nach neuesten Erkenntnissen zusammen aus:
- 73 % Vakuum-Energiedichte (Dunkle Energie)
- 23 % kalte dunkle Materie
- 4 % baryonische Materie, d. h die „normalen“ Elemente
- falls überhaupt, weniger als 1 % heiße dunkle Materie.
Herleitung der Friedmann-Gleichungen
Die Feldgleichungen der Allgemeinen Relativitätstheorie
Obwohl die Gravitation die schwächste der vier bekannten Wechselwirkungen ist, stellt sie auf größeren Maßstäben die dominierende Kraft im Universum dar und bestimmt dessen gesamte Entwicklung und Dynamik. Die gegenwärtig beste Beschreibung der Gravitation ist die Allgemeine Relativitätstheorie (ART). Diese verknüpft die Anziehungskraft der Materie eng mit der Krümmung und Dynamik der Raumzeit.
Der Übersichtlichkeit halber wird bei Berechnungen in der ART die Lichtgeschwindigkeit und die newtonsche Gravitationskonstante gleich 1 gesetzt („geometrische Einheiten“), so dass diese Größen nicht mehr explizit im Formalismus auftauchen. Die Feldgleichungen der ART lauten dann:
Hierin beschreibt der Einstein-Tensor G die Geometrie der Raumzeit, während der Energie-Impuls-Tensor T alle Materie- und Energiefelder umfasst. g stellt die relativistische Verallgemeinerung des metrischen Tensors
- (ημν) = diag( − 1,1,1,1)
für die statische und flache Minkowski-Raumzeit auf gekrümmte Raumzeiten dar. Λ steht für die kosmologische Konstante. Letztere wird oft als Vakuumenergie interpretiert, welche dem virtuellen Teilchenzoo entspringt, ihre tatsächliche Natur ist allerdings weiterhin ungeklärt.
Exakte Lösungen für die Feldgleichungen wurden bisher nur für hochsymmetrische Materieverteilungen gefunden. Das Problem besteht darin, für eine Materie- und Energieverteilung T eine passende Metrik g zu finden, aus der sich der Einsteintensor G in komplexer Weise zusammensetzt.
Die Metrik kann über das sogenannte Linienelement dargestellt werden,
wobei eine Summation über identische, hoch- und tiefgestellte Indizes impliziert ist (Einsteinsche Summenkonvention).
Lösung der Feldgleichungen für ein symmetrisches Universum
Die Materieverteilung im Universum ist auf geringen Entfernungen sehr unregelmäßig, erscheint allerdings ab mehreren hundert Megaparsec zunehmend isotrop, das heißt in alle Richtungen gleich aussehend. Unter der Annahme, dass ein Beobachter im Universum in keiner Weise privilegiert ist (kopernikanisches Prinzip), leitet sich daraus unmittelbar ab, dass das Universum von jedem Standpunkt aus isotrop aussieht und damit auch homogen ist. Dies ist auch als Kosmologisches Prinzip bekannt.
Howard Percy Robertson (1935) und Arthur Geoffrey Walker (1936) fanden unabhängig voneinander eine Lösung für die Feldgleichungen für den Fall eines solchen idealisierten Kosmos mit konstanter Krümmung. Das Linienelement dieser Metrik, welches bereits 1922 von Friedmann benutzt wurde, lautet
Hierbei stellt w die „mitbewegte“ Radialkoordinate dar, t die Eigenzeit eines „mitbewegten Beobachters“, a(t) den Expansionsfaktor des Universums, und θ und φ kennzeichnen die beiden Winkelkoordinaten, analog zu einem sphärischen Koordinatensystem. Ein mitbewegter Beobachter folgt der Expansion des Universums, seine mitbewegte Radialkoordinate behält hierbei ihren numerischen Wert.
Die Funktion fK(w) unterscheidet zwischen dreidimensionalen raumartigen Hyperflächen konstanter Zeit t mit positiver, verschwindender, oder negativer Krümmung K. Unter einer solchen Hyperfläche versteht man alle Ereignisse, die zur gleichen kosmologischen Zeit stattfinden. Zum Beispiel formen unsere Milchstraße und alle anderen Galaxien heute eine raumartige Hyperfläche. Nur sehen wir diese Galaxien aufgrund der Lichtlaufzeit nicht in diesem heutigen Zustand, sondern in einem individuellen und bereits vergangenen Zustand. Die raumartige Hyperfläche, welche sie aufspannen, ist daher keiner Beobachtung zugänglich.
fK(w) ist gegeben durch
Durch Umskalieren der Radialkoordinate w und Neudefinition des Skalenfaktors a lässt sich der Krümmungsparameter K auf einen der Werte -1, 0 oder 1 festlegen.
Mit dieser Metrik und den Feldgleichungen werden dann die Friedmann-Gleichungen abgeleitet. Details finden sich unter anderem in Gravitation (Misner, Thorne und Wheeler, 1973).
In einem ersten Schritt werden die Zusammenhangskoeffizienten (Christoffel-Symbole)
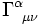 aus der Metrik berechnet. Sie erlauben den Vergleich eines Tensorfeldes zwischen zwei benachbarten Ereignissen in einer gekrümmten Raumzeit,
aus der Metrik berechnet. Sie erlauben den Vergleich eines Tensorfeldes zwischen zwei benachbarten Ereignissen in einer gekrümmten Raumzeit,Partielle Ableitungen werden hierbei geschrieben als
Hieraus leitet sich der Riemann-Tensor R ab, welcher die Krümmung der Raumzeit beschreibt als
Schließlich ergibt sich der Einstein-Tensor G aus R und der Metrik g,
Setzt man das Robertson-Walker-Linienelement in diese drei Gleichungen ein, und benutzt die beiden Zusammenhänge
so findet sich ein diagonaler Einstein-Tensor. Die Diagonalität rührt hierbei direkt aus der angenommenen Isotropie und Homogenität der Materieverteilung im Universum. G lautet
(t,w,θ,φ) stellen hierbei die (0,1,2,3)-Komponenten dar.
Die Friedmann-Gleichungen
Da die Nicht-Diagonal-Elemente des Einsteintensors verschwinden, muss dasselbe auch für den Energie-Impuls-Tensor gelten. Aus der Forderung nach Isotropie folgt weiterhin, dass sein räumlicher Anteil ein Vielfaches des Einheitstensors sein muss
wobei ρ = ρ(t) und p = p(t) die homogene Dichte und Druck darstellen, die nur von der Zeit abhängen.
Setzt man diese Größen in die Feldgleichungen ein, so erhält man die beiden Friedmann-Gleichungen
Die zweite Gleichung wird (insbesondere im englischsprachigen Raum) auch als Raychaudhuri-Gleichung bezeichnet. Leitet man erstere nach der Zeit ab und setzt sie in die zweite ein, so ergibt sich die Energieerhaltung in der Form
Die erste Friedmann-Gleichung genügt daher, um zusammen mit dem Energieerhaltungssatz die globale Entwicklung des Universums zu beschreiben.
Die Gleichungen am Anfang des Artikels ergeben sich, indem man die Kosmologische Konstante in die Energiedichte und den Druck absorbiert.
Spezielle Lösungen der Gleichungen
Wir haben nun zwei Gleichungen für die drei Unbekannten a,ρ und p. Um eine eindeutige Lösung zu erhalten, ist daher eine weitere Gleichung, die Zustandsgleichung der Materie, nötig. Gewöhnliche (baryonische) Materie, Strahlung und die Kosmologische Konstante fungieren als Hauptquellen der Gravitation auf der rechten Seite der Feldgleichungen der ART. Die Materie kann hierbei als druckloser „Staub“ angesehen werden, d. h. die Teilchen bewegen sich kollisionsfrei mit nicht-relativistischen Geschwindigkeiten. Die Zustandsgleichungen dieser drei Bausteine lauten dann
- pd = 0
- pr = ρr / 3
- pΛ = − ρΛ.
Aus der Energieerhaltung ergibt sich der Zusammenhang zwischen Dichte ρ und Skalenfaktor a
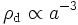
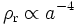
- ρΛ = const
Als Anfangswert für die erste Friedmann-Gleichung (auch als Friedmann-Lemaître-Gleichung bekannt) wird a(t0) = 1 verwendet, wobei t0 die kosmologische Zeit im Jetzt darstellt. Die Friedmann-Lemaître-Gleichung kann auch geschrieben werden als
wobei die Hubble-Funktion wie oben definiert wird als
Diese beschreibt die Expansionsrate des Universums, mit H0 = H(t0) zum heutigen Zeitpunkt. Weiterhin finden sich
welche die Materiedichte und Vakuumenergiedichte parametrisieren. Die Strahlungsdichte wird hier vernachlässigt, da sie mit a − 4 abfällt und daher gegenüber der Materiedichte rasch unbedeutend wird.
Löst man die Friedmann-Lemaître-Gleichung nach K für den Zeitpunkt t = t0, und setzt das erhaltene Ergebnis zurück ein, so erhält man die Friedmann-Lemaître-Gleichung in ihrer bekanntesten Form,
Für ein flaches Universum (1 − Ω0 − ΩΛ = 0) wie unseres, kann man eine explizite Lösung dieser Gleichung für den Skalenfaktor angeben: mit dem Verfahren der Variablentrennung lässt sich diese Differentialgleichung in ein Integral verwandeln, aus dem t(a) bestimmt wird zu
Dieser Ausdruck lässt sich invertieren. Wählt man t0 so, dass a(0) = 0 und das Universum somit einen kompakten Anfang besitzt, und benutzt man Ω0 = 1 − ΩΛ, so erhält man
Dieser Ausdruck beschreibt das Expansionsverhalten für ein flaches Universum mit kosmologischer Konstante. Peacock (2001) und Carroll (1992) haben einen identischen Ausdruck in anderer analytischer Form hergeleitet. Die über die Sonde WMAP gemessenen Schwankungen in der Hintergrundstrahlung erlauben Rückschlüsse auf die Geometrie unseres Universums. Demnach ist dieses flach, mit einem Materiedichteparameter Ω0 = 0.27, einem Vakuumdichteparameter ΩΛ = 0.73 und einer Hubblekonstante von H0 = 72km/s/Mpc.
Kosmologische Rotverschiebung und Entfernungsmaße
In dynamischen und gekrümmten Raumzeiten gibt es, im Gegensatz zu Euklidischen Räumen, kein eindeutiges Entfernungsmaß mehr. Es existieren verschiedene, gleichberechtigte Entfernungsdefinitionen, basierend auf dem Linienelement eines Photons und mit der kosmologischen Rotverschiebung als gemeinsamen Nenner.
Weblinks
Literatur
- Caroll, S. M., Press, W. H., Turner, E. L. 1992, Ann. Rev. Astr. Astrophys., 30, 499
- Friedmann, A. 1922, Zeitschrift für Physik, 10, 377
- Misner, C., Thorne, K. S., Wheeler, J. A.: Gravitation, W. H. Freeman, San Francisco, 1973. ISBN 0-7167-0344-0.
- Peacock, J. A. 2001, Cosmological Physics, Cambridge University Press, ISBN 0-521-42270-1.
- Robertson, H. P. 1935, Astrophysical Journal, 82, 284
- Walker, A. G. 1936, Proc. Lond. Math. Soc. (2), 42, 90
Wikimedia Foundation.

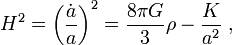
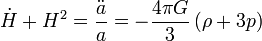

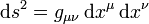
![\mathrm{d} s^{2} = -\mathrm{d} t^{2} + a^{2}(t)\left[\mathrm{d} w^2 + f_K^{\,2}(w)\left(\mathrm{d}\theta^2 +
\mathrm{sin}^2\theta\, \mathrm{d} \phi^2\right)\right]\,.](/pictures/dewiki/101/e31a79af942e79abee66890aeb930474.png)
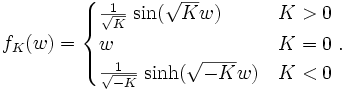
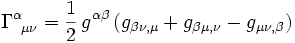
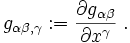
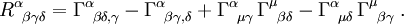
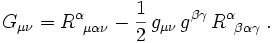
![[f'_K(w)]^2 = 1 - K f_K^{\,2}(w)](/pictures/dewiki/55/786ad939f309710b164031013d335838.png)