19-EDO

Ein Neunzehnstufiges Tonsystem organisiert die musikalischen Tonhöhen in 19 verschiedenen Stufen pro Oktavraum. Sind diese Stufen gleich groß, spricht man von der gleichmäßigen Neunzehntönigen Stimmung, in der direkt benachbarte Töne einen Höhenunterschied von ca. 63,16 Cent bzw. ein Frequenzverhältnis von

$\frac{f_2}{f_1} = \sqrt[19] \tfrac 2 1 \approx 1{,}037155$

haben.

Alle temperierten neunzehntönigen Stimmungen verfügen über dieselbe spezifische Enharmonik, die sich deutlich von der bei 12-tönigen Temperierungen gewohnten unterscheidet. So klingen die z. B. Töne Fis und Ges tatsächlich verschieden hoch, und bei einem 19-stufigen Quintenzirkel könnte man die Nahtstelle beispielsweise zwischen Ais und Fes legen. Hieraus resultieren von der klassischen 12-Stufigkeit differierende Modulationswege.

Ein weiterer wesentlicher Aspekt, dass nämlich einige grundlegende Intervalle in 19-tönigen Systemen gut angenähert werden können, wurde bereits im ausgehenden 16. Jahrhundert offenbar, als man diese aus dem Bemühen um eine optimale Mitteltönige Stimmung erstmals folgerte.

Erste Ansätze im 16. Jahrhundert

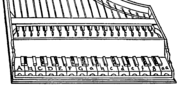Tastatur eines 19-stufigen Cembalos aus Le istituzioni harmoniche (Ausgabe 1573) von Gioseffo Zarlino

Im 16. Jahrhundert versuchten mehrere Theoretiker (mit Bezug auf die antike Musik Griechenlands, deren Tonarten sie wiederzugeben versuchten), den Kompromiss zwischen reinen Intervallen und den Verschiebungen durch zusätzliche Töne innerhalb der Oktave auszugleichen und enharmonische „Varianten“ zu den vorhandenen zwölf Tönen mit zusätzlichen Tasten (bei einer Tastatur) zu realisieren. Der Versuch, immer genauere Differenzierungen für enharmonische Tonleitern zu finden, führte zu Vorschlägen für 19-, aber auch für 24- und 36-stufige Tonleitern und Tastaturen, für die auch Instrumente gebaut wurden. 19-stufige Cembali waren im 16. Jahrhundert offenbar recht häufig. Dies ergab die Möglichkeit, mehr Intervalle relativ „rein“ erklingen zu lassen und somit mehr Tonarten „harmonisch“ klingend spielen zu können. Bei all dem gelang allerdings die mathematische Darstellung problemloser als die Stimmpraxis und der Bau entsprechender Instrumente.

Bereits 1558 erwähnte der italienische Komponist und Theoretiker Gioseffo Zarlino in seinem Werk Le istituzioni harmoniche eine Stimmung, die sich auf neunzehn Tonschritte innerhalb der Oktave bezog, ohne genau darauf einzugehen. Es handelt sich hierbei offenbar um die 1577 von dem Theoretiker Francisco de Salinas vorgeschlagene ¹/₃-Komma Mitteltönige Stimmung, die die damals üblichen zwölf Töne der Tonleiter - C, Cis, D, Es, E, F, Fis, G, Gis, A, B und H - um sieben weitere enharmonische Varianten - His, Des, Dis, Eis, Ges, As und Ais - ergänzt. Nach zeitgenössischem Zeugnis vermochte der blinde Salinas in dieser Temperatur sehr gewandt auf einem nach seinen Plänen konstruierten 19-stufigen Instrument zu spielen. Klaus Lang schreibt hierzu^[1]

„In dieser Stimmung sind die Quinten und großen Terzen um 1/3-(syntonisches) Komma verkleinert, während die großen Sexten rein bleiben. Zarlino meint selbst, dass diese Methode nicht so gut klinge wie die beiden anderen Methoden. Eine interessante Eigenschaft dieser Temperierungsmethode ist aber, dass sich, wenn man eines, der im 16. Jahrhundert relativ weit verbreiteten Instrumente mit 19 Stufen pro Oktave mit ihrer Hilfe einstimmt, der Quintenzirkel schließen lässt, also die Wolfsquinte beseitigt wird“

Die Chanson Seigneur Dieu ta pitié des französischen Komponisten Guillaume Costeley ist für eine 19-stufiges Tonsystem komponiert; denn Costeley berichtete 1570 davon, dass er diese chromatisch-enharmonische chanson spirituell „vor gut zwölf Jahren“ („il y bien douze ans“), also etwa 1557, als Übung im Gebrauch einer 19-stufigen Tonleiter komponiert habe. Er erläuterte nebenbei auch recht detailliert, wie man 19-stufige Tasteninstrumente zu bauen habe, und dachte dabei an eine gleichstufige Teilung der Oktav.

Gleichstufige Unterteilung der Oktave seit dem 19. Jahrhundert

Im 19. Jahrhundert begann die Forschung über Alternativen zur 12-tönigen gleichstufigen Stimmung. Um „reinere“ Intervalle zu erzeugen, wurde neben 31-, 43-, 50- und 53-stufigen Einteilungen der Oktave aus pragmatischen Gründen die 19-stufige besonders untersucht, sie ist die nächstliegende. Der Theoretiker Wesley Woolhouse propagierte in seinem Essay on Musical Intervals, Harmonics, and the Temperament of the Musical Scale 1835 neben anderen ein gleichstufig gestimmtes Tonsystem, welches die Oktave (entgegen der herkömmlichen Strömung) in 19 (statt in 12) gleiche Intervalle teilt. Das bemerkenswerte daran ist, dass für große und kleine Terzen und Sexten Frequenzverhältnisse entstehen, die um einiges näher am „reinen“ Intervall sind, als die in der üblichen gleichstufigen Stimmung. Alle anderen Intervalle sind allerdings weiter von ihren reinen Äquivalenten entfernt.

Für die gleichmäßige neunzehnstufige Stimmung existieren eine ganze Reihe von Kompositionen sowohl mit klassischem Anspruch als auch im Rock- und Pop-Sektor. Die Entwicklung im Bereich elektronischer Musikinstrumente bzw. computergestützter Systeme zur Soundsynthese geben Kompositionen in diesem und anderen alternativen Stimmungen erheblichen Vorschub.

Das Tonmaterial

Die mathematische Vorschrift zur Bestimmung der Frequenz eines Tons der 19-stufigen gleichsschwebenden Stimmung lautet

$f(i) = f(0) \cdot 2^{i/19} \,$,

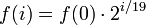wobei f(0) die Frequenz eines beliebigen Bezugston, f(i) die Frequenz des Tones, der um i 19tel-Oktav-Schritte höher liegt.

Der kleinste darstellbare Tonunterschied des Systems ist also

$f(1) = f(0) \cdot 2^{1/19} = \sqrt[19]{2^1} \approx 1{,}037155 \approx 63{,}16\,\mathrm{Cent}$

Wie in der zwölfstufigen gleichschwebenden Stimmung, lassen sich auch für die neunzehnstufige gleichsschwebende Stimmung Intervallgrößen als Vielfache des kleinsten darstellbaren Intervalls beschreiben. Man erhält folgende Werte für Schritt-Intervalle^[2]:

Intervallname	Beispiel	19-stufige Stimmung	12-stufige Stimmung
Diatonischer Ganzton	C−D	3 Schritte	2 Schritte
Diatonischer Halbton	E−F	2 Schritte	1 Schritt
Chromatischer Halbton	F−Fis	1 Schritt	1 Schritt

Eigenschaften ausgewählter Intervalle

Die in der klassischen Musik als Konsonanzen aufgefassten Intervalle der Reinen Stimmung werden von der 19-stufigen Stimmung teilweise besser (Terzen und Sexten), teilweise weniger gut (Quarte und Quinte) wiedergegeben. Hierzu eine tabellarische Gegenüberstellung (die Differenzen werden in Cent angegeben, die jeweils „bessere“ Annäherung ist hervorgehoben):

Intervall	Prime	kl. Terz	gr. Terz	Quarte	Quinte	kl. Sexte	gr. Sexte	Oktave
Diff. 19-stufig	0	0,15	-7,37	7,22	-7,22	7,37	-0,15	0
Diff. 12-stufig	0	-15,64	13,69	1,96	-1,96	-13,69	15,64	0

Die folgende Tabelle zeigt die Werte aller Intervalle, in gleichstufiger und reiner Stimmung sowie deren Abweichung voneinander in Cent:

Intervall	Gleichstufig temperiertes Intervall	Reines Intervall	Differenz in Cent 2)	Differenz in Cent der zwölfstufigen gleichstufigen Stimmung zum reinen Intervall 2)
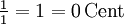
Prime	$\sqrt[19]{2^0} = 1 = 0\,\mathrm{Cent}$	$\tfrac{1}{1} = 1 = 0\,\mathrm{Cent}$	0 Cent	0 Cent
Übermäßige Prime und verminderte Sekunde	$\sqrt[19]{2^1} \approx 1{,}037155 \approx 63{,}16\,\mathrm{Cent}$
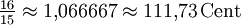
Kleine Sekunde	$\sqrt[19]{2^2} \approx 1{,}075691 \approx 126{,}32\,\mathrm{Cent}$	$\tfrac{16}{15} \approx 1{,}066667 \approx 111{,}73\,\mathrm{Cent}$	14,58 Cent	-11,73 Cent
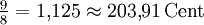
Große Sekunde	$\sqrt[19]{2^3} \approx 1{,}115658 \approx 189{,}47\,\mathrm{Cent}$	$\tfrac{9}{8} = 1{,}125 \approx 203{,}91\,\mathrm{Cent}$	-14,44 Cent	-3,91 Cent
Übermäßige Sekunde und verminderte Terz	$\sqrt[19]{2^4} \approx 1{,}157110\approx 252{,}63\,\mathrm{Cent}$
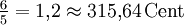
Kleine Terz	$\sqrt[19]{2^5} \approx 1{,}200103 \approx 315{,}79\,\mathrm{Cent}$	$\tfrac{6}{5} = 1{,}2 \approx 315{,}64\,\mathrm{Cent}$	0,15 Cent	-15,64 Cent
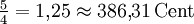
Große Terz	$\sqrt[19]{2^6} \approx 1{,}244693 \approx 378{,}95\,\mathrm{Cent}$	$\tfrac{5}{4} = 1{,}25 \approx 386{,}31\,\mathrm{Cent}$	-7,37 Cent	13,69 Cent
Übermäßige Terz und verminderte Quarte	$\sqrt[19]{2^7}\approx 1{,}290939 \approx 442{,}11\,\mathrm{Cent}$
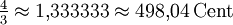
Quarte	$\sqrt[19]{2^8} \approx 1{,}338904 \approx 505{,}26\,\mathrm{Cent}$	$\tfrac{4}{3} \approx 1{,}333333 \approx 498{,}04\,\mathrm{Cent}$	7,22 Cent	1,96 Cent
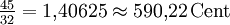
Übermäßige Quarte 1)	$\sqrt[19]{2^9} \approx 1{,}388651 \approx 568{,}42\,\mathrm{Cent}$	$\tfrac{45}{32} = 1{,}40625 \approx 590{,}22\,\mathrm{Cent}$	-21,8 Cent	9,78 Cent
Verminderte Quinte	$\sqrt[19]{2^{10}} \approx 1{,}440247 \approx 631{,}58\,\mathrm{Cent}$
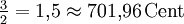
Quinte	$\sqrt[19]{2^{11}} \approx 1{,}493759 \approx 694{,}74\,\mathrm{Cent}$	$\tfrac{3}{2} = 1{,}5 \approx 701{,}96\,\mathrm{Cent}$	-7,22 Cent	-1,96 Cent
Übermäßige Quinte und verminderte Sexte	$\sqrt[19]{2^{12}} \approx 1{,}549260 \approx 757,89\,\mathrm{Cent}$
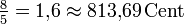
Kleine Sexte	$\sqrt[19]{2^{13}} \approx 1{,}606822 \approx 821{,}05\,\mathrm{Cent}$	$\tfrac{8}{5} = 1{,}6 \approx 813{,}69\,\mathrm{Cent}$	7,37 Cent	-13,69 Cent
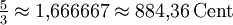
Große Sexte	$\sqrt[19]{2^{14}} \approx 1{,}666524 \approx 884{,}21\,\mathrm{Cent}$	$\tfrac{5}{3} \approx 1{,}666667 \approx 884{,}36\,\mathrm{Cent}$	-0,15 Cent	15,64 Cent
Übermäßige Sexte und verminderte Septime	$\sqrt[19]{2^{15}} \approx 1{,}728444 \approx 947{,}37\,\mathrm{Cent}$
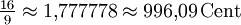
Kleine Septime	$\sqrt[19]{2^{16}} \approx 1{,}792664 \approx 1010{,}53\,\mathrm{Cent}$	$\tfrac{16}{9} \approx 1{,}777778 \approx 996{,}09\,\mathrm{Cent}$	14,44 Cent	3,91 Cent
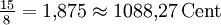
Große Septime	$\sqrt[19]{2^{17}} \approx 1{,}859270 \approx 1073{,}68\,\mathrm{Cent}$	$\tfrac{15}{8} = 1{,}875 \approx 1088{,}27\,\mathrm{Cent}$	-14,58 Cent	11,73 Cent
Übermäßige Septime und verminderte Oktave	$\sqrt[19]{2^{18}} \approx 1{,}928352 \approx 1136{,}84\,\mathrm{Cent}$
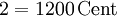
Oktave	$\sqrt[19]{2^{19}} = 2 = 1200\,\mathrm{Cent}$	$2 = 1200\,\mathrm{Cent}$	0 Cent	0 Cent
Anmerkungen: 1) Übermäßige Quarte, mitunter auch als Tritonus bezeichnet, definiert als: Große Terz (5/4) plus Große Sekunde (9/8). Das ist gleichbedeutend mit: Quinte (3/2) minus diatonischer Halbton (16/15). 2) Ist die Differenz negativ, so ist das gleichtemperierte Intervall enger als das reine.

Siehe auch

• Quintenzirkel
• Cent
• Viertelton-Musik

Quellen und Literatur

Quellen

1. ↑ Klaus Lang, Auf Wohlklangswellen durch der Töne Meer. Temperaturen und Stimmungen zwischen 11. und 19. Jahrhundert. Beiträge zur elektronischen Musik 10, Graz 1999, S.62
2. ↑ In der Musikpraxis werden Intervalle mitunter nach absoluter Größe unterschieden: alles was kleiner oder gleich der Sekunde ist, wird Schritt genannt, größere Intervalle Sprung; diese Unterscheidung wird z.B. in den Regeln des Kontrapunkts beachtet.

Literatur

• Klaus Lang: Auf Wohlklangswellen durch der Töne Meer. Temperaturen und Stimmungen zwischen 11. und 19. Jahrhundert. Beiträge zur elektronischen Musik 10, Graz 1999 (pdf)
• Mark Lindley: Stimmung und Temperatur. In Frieder Zaminer (Hrsg.): Geschichte der Musiktheorie. Bd. 6. Hören Messen und Rechnen in der frühen Neuzeit, S. 109-332, Darmstadt 1987

Weblinks

Zum 16. Jahrhundert

• Encyklopedia of Microtonal Music Theory, daraus:
  • 19-tone equal-temperament and 1/3-comma meantone
  • 2/7-comma meantone
• Guillaume Costeley: Seigneur dieu ta pitié:
  • Noten (ohne Text) und Tonaufnahme (mit elektronisch simulierter Orgel)
  • Essay (englisch, siehe das Postscript)

Zum 20. und 21. Jahrhundert

(alle Weblinks auf Englisch)

• Bucht, Saku and Huovinen, Erkki, Perceived consonance of harmonic intervals in 19-tone equal temperament (pdf)
• Darreg, Ivor, A Case for Nineteen
• Howe, Hubert S. Jr., 19-Tone Theory and Applications
• Sethares, William A., Tunings for 19 Tone Equal Tempered Guitar

Tonbeispiele

• Jacob Barton: Foum (mp3)
• Jeff Harrington: Prelude 1 for 19ET Piano (mp3)
• Jeff Harrington: Prelude 2 for 19ET Piano (mp3)
• Jeff Harrington: Prelude 3 for 19ET Piano (mp3)
• Aaron Kristler: Juggler (ogg)