Reine Stimmung

Die Reine Stimmung (auch natürliche oder harmonische Stimmung) entstand mit dem Aufkommen der Mehrstimmigkeit und benutzt in den Akkordverbindungen die reinen Intervalle Oktave, Quinte und Terz. Sie kann mit der menschlichen Stimme und vergleichbaren Instrumenten verwirklicht werden, jedoch auf üblichen Tasteninstrumenten mit zwölf Tasten pro Oktave nur eingeschränkt, da beim Übergang zu benachbarten Tonarten nicht nur jeweils ein Ton um einen Halbton verschoben (und dies durch die Notenbezeichnung angezeigt) wird, sondern zudem ein weiterer Ton um ein syntonisches Komma verändert ist (siehe Modulationen in reiner Stimmung). Die Stimmung oder Temperierung für Tasteninstrumente wandelte sich daher über die mitteltönigen Stimmungen und wohltemperierten Stimmungen bis hin zur gleichstufigen Stimmung, vor allem beim Klavier.

In der Mehrstimmigkeit trat die Reine Stimmung in Konkurrenz zur pythagoreischen Stimmung, die heute häufig noch beim melodischen Solovortrag anzutreffen ist.

Manchmal werden bei der reinen Stimmung auch Intervalle höherer Ordnung miteinbezogen, wie sie sich aus der Obertonreihe ergeben, beispielsweise die Naturseptime.

Tonarten in reiner Stimmung

Mit dem Aufkommen der in der Mehrstimmigkeit sich bildenden Akkordverbindungen wurde bald die Terz mit dem Frequenzverhältnis ⁵/₄ als Konsonanz anerkannt und neben der Oktave (Frequenzverhältnis ²/₁) und Quinte (Frequenzverhältnis ³/₂) rein intoniert. Dieser Übergang war spätestens mit der polyphone Musik Palestrinas und dem protestantischen mehrstimmigen Choral abgeschlossen.

Es bildeten sich reine Tonarten heraus. Diese spielen in der Aufführungspraxis der Musik der Renaissance und des Barocks beim reinen Intonieren beispielsweise von A-cappella-Chören, Streichquartetten oder guten Orchestern eine ausschlaggebende Rolle. Bei reiner Intonation und guter Akustik erhält man betonte Bässe (wegen der Differenztöne) und kristallklaren Klang (wegen der Übereinstimmung von Obertönen). ^[1] In den mitteltönigen Stimmungen, die jahrhundertelang dann vorherrschte, wird diese Stimmung mit den reinen Terzen am besten verwirklicht - allerdings nur für eine begrenzte Zahl von Tonarten.

A-Dur Kadenz	rein Anhören?/i (Keine Schwebungen.)	mitteltönig Anhören?/i (Geringe Schwebungen, durch die leicht "verstimmten" Quinten bedingt. Siehe: mitteltönige Quinten.)	gleichstufig Anhören?/i (Heftige Schwebungen - etwa zehn mal schneller als bei mitteltönig, hauptsächlich durch die "verstimmte" Terz bedingt.)

Die Oktave, die Quinte und die große Terz bilden die Grundintervalle der reinen Stimmung. Alle weiteren Intervalle lassen sich aus diesen Grundintervallen zusammensetzen. Man nennt deshalb dieses System auch Quint-Terz-System.

Tabelle der Frequenzverhältnisse der Dur- und Molltonleiter in reiner Stimmung

Reine Tonleitern beruhen auf folgenden Frequenzverhältnissen:

C-Dur (als Beispiel)		C		D		E		F		G		A		H		c
Intervall Frequenzverhältnis zum Grundton		Prim 1/1		große Sekunde 9/8		große Terz 5/4		Quarte 4/3		Quinte 3/2		große Sext 5/3		große Septime 15/8		Oktave 2/1
Frequenzverhältnis benachbarter Töne			9/8		10/9		16/15		9/8		10/9		9/8		16/15
c-Moll (als Beispiel)		C		D		Es		F		G		As		B		c
Intervall Frequenzverhältnis zum Grundton		Prim 1/1		große Sekunde 9/8		kleine Terz 6/5		Quarte 4/3		Quinte 3/2		kleine Sext 8/5		kleine Septime 9/5		Oktave 2/1
Frequenzverhältnis benachbarter Töne			9/8		16/15		10/9		9/8		16/15		9/8		10/9

Die Akkorde der Tonika C-E-G bzw. C-Es-G, der Subdominante F-A-c bzw. F-As-c und der Dominante G-H-d bzw. G-B-d (in moll) bestehen aus reinen Quinten und Terzen. Bei den Tonleitern in reiner Stimmung ist zu beachten, dass es zwei Arten von Ganztönen gibt, zum Beispiel C nach D mit dem Frequenzverhältnis ⁹/₈ und D nach E mit dem Frequenzverhältnis ¹⁰/₉.

Dadurch weichen diese Tonleitern unüberhörbar von den Tonleitern in pythagoreischer Stimmung und auch von der Tonleiter in gleichstufigen Stimmung ab, bei der jeder Halbton genau ein Zwölftel der Oktave ausmacht und ein Ganzton genau zwei Halbtönen entspricht.

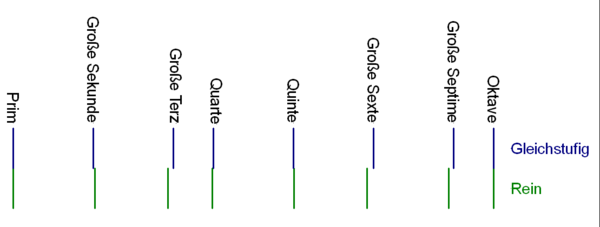Unterschied zwischen reiner und gleichstufiger Dur-Tonleiter. Die große Terz, die große Sexte und die große Septime sind bei der gleichstufigen Stimmung zu groß.

Unterschied zwischen reiner und gleichstufiger Moll-Tonleiter. Die kleine Terz, die kleine Sexte und die kleine Septime sind bei der gleichstufigen Stimmung zu klein.

Die große Terz

Grundlegend ist die charakteristische reine Terz mit dem Frequenzverhältnis ⁵/₄. Die mitteltönigen Stimmung mit ihren vielen reinen Terzen verwirklichte fast vollkommen die reine Stimmung für Tasteninstrumente - allerdings nur für eine begrenzte Zahl von Tonarten.

Anhören rein?/i Anhören mitteltönig?/i Anhören pythagoreisch?/i Anhören gleichstufig?/i

Die reine Terz mit dem Frequenzverhältnis 5/4 wurde nun (im Gegensatz zur pythagoreischen Terz mit dem Frequenzverhältnis 81/64) als Konsonanz empfunden. Es dauerte mehrere Jahrhunderte, bis man die (der pythagoreischen Terz ähnliche) gleichstufige Terz akzeptierte. In reiner und mitteltöniger Stimmung hört man bei der reinen Terz (386 Cent) keine Schwebung. Bei der mitteltönigen Stimmung hört man die etwas temperierte Quinte im zweiten Akkord in einer geringfügigen Schwebung. Die "geschärfte" Terz in gleichstufiger (400 Cent) oder gar pythagoreischer (408 Cent) Stimmung mit einer starken Schwebung wird als Reibung empfunden. (Siehe dazu auch das Beispiel der großen Terz mit verstärktem Differenzton).

Hinweis: Reine Intervalle sind durch ganzzahlige Frequenzverhältnisse charakterisiert, temperierte Intervalle haben dagegen meist ein irrationales Frequenzverhältnis. Deshalb erfolgt der Größenvergleich mit der Einheit Cent.

F-Dur-Kadenz
Anhören rein?/i	Die reine Terz im Sopran des Akkords - wie hier im ersten, dritten und letzten Akkord - erscheint dem an die gleichstufige Stimmung gewöhnten Ohr als zu tief intoniert. Der klare Klang dagegen überzeugt. Zum Vergleich: Anhören mitteltönig?/i     Anhören gleichstufig?/i

Probleme bei Tasteninstrumenten

Dass sich bei Modulationen nicht nur Töne um einen Halbton verändern (was durch die Notenbezeichnung sichtbar wird), sondern manche Töne sich auch um ein syntonisches Komma verändern (was in der Notenbezeichnung nicht sichtbar ist), wird beim Thema Modulationen gezeigt. Diese Flexibilität in der Anpassung der Tonhöhe ist nur der menschlichen Stimme oder vergleichbaren Instrumenten vorbehalten.

Deshalb ist bei (nicht elektronischen) Tasteninstrumenten eine reine Intonation in allen Tonarten nicht möglich.

Diese Problematik spielte in der abendländischen Musikpraxis beim Stimmen von Tasteninstrumenten mit zwölf Tasten pro Oktave eine große Rolle.

Die lange Zeit vorherrschenden mitteltönigen Stimmungen mit vielen reinen Terzen nähern die reine Stimmung hervorragend an, allerdings nur (in der 1/4-Komma mitteltönigen Stimmung) in den Tonarten B-, F-, C-, G-, D- und A-Dur, sowie g-, d-, a-, e-, h- und fis-moll. In diesen Tonarten erklingen die Akkorde der Tonika, der Subdominante und der Dominante in den Terzen rein und in den Quinten nur mit geringfügigen als "farbliche Nuancierung" empfundene Schwebungen. Anzuhören: mitteltönige Quinten.

Um die Tonarten des gesamten Quintenzirkels spielbar zu machen, wurden die mitteltönige Stimmungen zu wohltemperierten Stimmungen so erweitert, dass die Tonarten des gesamten Quintenzirkels spielbar wurden. Dies wurde aber nur ermöglicht, indem man die reinen Terzen je nach Tonart mehr oder weniger wieder den pythagoreischen Terzen annäherte (schärfte). Vor allem beim Klavier hat sich die gleichstufigen Stimmung schließlich durchgesetzt, bei der es keine "Tonartencharakter" mehr gibt.

Der Cellist Pablo Casals äußert sich zu diesem Problem ("The Way They Play" 1972): Erschrecke nicht, wenn Du eine andere Intonation als das Klavier hast. Das liegt am Klavier, das verstimmt ist.

Der Intonationsunterschied zwischen reiner Stimmung und gleichstufiger Stimmung ist vernachlässigbar bei den Quinten (rein: 702 Cent, gleichstufig 700 Cent) aber durchaus hörbar - und dies wird häufig übersehen - in den Terzen (Große Terz rein: 386 Cent, gleichstufig: 400 Cent. Kleine Terz rein: 316 Cent, gleichstufig 300 Cent).

Zu beobachten ist, dass historisch gestimmte Cembali und Orgeln wieder an Bedeutung gewinnen.

diatonische Harmonika

Die diatonische Harmonika mit ein bis drei Reihen wurde üblicherweise in ihrem möglichen Tonvorrat in vielen Fällen fast rein gestimmt, oder die Stimmung war einer der mitteltönigen Stimmungen angenähert. Erst in den letzten Jahrzehnten wurde in vielen Fällen die gleichstufige Stimmung verwendet. Auch heute bevorzugen einzelne Hersteller traditionelle Stimmungen für die steirische Harmonika. Einreihige Instrumente für Cajun-Musik oder manche Mundharmonikas sind auch der reinen Stimmung zumindest angenähert. Wenn auf mehrreihigen Instrumenten die reine Stimmung zur Anwendung kommt, stehen bei manchen Tönen Alterierungen mit geringfügigen Tonhöhenunterschieden zur Verfügung, zum Beispiel zwei Ds, wobei es aber von der jeweiligen Spielreihe abhängt, wie die Töne zueinander greifbar sind. Die doppelt vorkommenden Töne sind pro Reihe rein oder mit Terzen gestimmt, die nur eine sehr geringe Schwebung aufweisen. Somit ergibt sich durch die Quartabstände von Reihe zu Reihe insgesamt ein Tonnetz. Die Möglichkeiten sind damit nicht so dramatisch wie mit einem Reintonistrument aber doch beachtlich, wenn ein Musiker weiß wie man diese Eigenheiten auch nutzt.

Modulationen erfordern eine Anpassung der Tonhöhe

Wenn im folgenden von reinen Akkorden die Rede ist, ist gemeint, dass vorkommenden Quinten (Frequenzverhältnis³/₂), große Terzen (Frequenzverhältnis⁵/₄) und kleine Terzen (Frequenzverhältnis⁶/₅) rein sind.

Faustregel: Bei einer Modulation in eine Nachbartonart (Dur oder moll) ändern sich zwei Töne, einer davon erkennbar mit Vorzeichenwechsel, der andere geringfügig um ein syntonisches Komma. (Das ist ungefähr ¹/₅ Halbton.)

Modulation in Richtung Subdominante

Faustregel: Der 2. und 7. Ton ändern sich

Beispiel: Modulation von C-Dur über a-moll nach F-Dur

C-Dur

Name des Tones		C		D		E		F		G		A		H		c
Frequenz		264		297		330		352		396		440		495		528
Frequenzverhältnis			9/8		10/9		16/15		9/8		10/9		9/8		16/15

Die Akkorde der Tonika C-E-G, der Subdominante F-A-c und der Dominante G-H-d sind rein.

a-moll (absteigend) Zum besseren Vergleich nicht in der Reihenfolge A-H-c-d-e-f-g-a sondern wieder C-D-E-F-G-A-H-c.

Name des Tones		C		D(!)		E		F		G		A		H		c
Frequenz		264		293,3(!)		330		352		396		440		495		528
Frequenzverhältnis			10/9		9/8		16/15		9/8		10/9		9/8		16/15

Hier sind die Akkorde der Tonika A-c-e, der Subdominante D-F-A (in C-Dur: die II. Stufe) und der Dominante (in moll) E-G-H rein.

Wie man hier erkennen kann, bedeutet in C-Dur der Akkord der II. Stufe D-F-A den Beginn eine Modulation in Richtung Subdominante. (Dieser Akkord kann jedoch auch als Doppeldominante - oft verdeutlicht als D-Fis-A gedeutet werden.)

F-Dur

Name des Tones		C		D(!)		E		F		G		A		B(!)		c
Frequenz		264		293,3(!)		330		352		396		440		469,3(!)		528
Frequenzverhältnis			10/9		9/8		16/15		9/8		10/9		16/15		9/8

Hier sind die Akkorde der Tonika F-A-c, der Subdominante B-d-f und der Dominante C-E-G rein.

Im Vergleich zu C-Dur hat sich bei F-Dur das H um einen Halbton zu B erniedrigt (das zeigt auch die Notenbezeichnung), aber auch - wie bei der Modulation von C-Dur nach a-moll - hat sich das D um ein syntonisches Komma (Frequenzverhältnis ⁸¹/₈₀$\widehat{=}$21,5 Cent) geändert. Sonst bestünde die Subdominante in F-Dur B-d-f bzw. in A-moll D-F-A nicht mehr aus reinen Terzen und Quinten.

Nebenbei bemerkt: In der Kirchtonart Jonisch (heute Dur) war schon immer der 2. und 7. Ton schwankend. (Oft wurde bekanntlich statt dem Ton B der Ton H intoniert, aber auch das D wurde mal als reine Quinte zu G, ein anderes Mal als reine Quarte zu A (ein Komma tiefer) intoniert.

Beispiel: Modulation von c-moll nach f-moll

Hier erniedrigt sich D um einen Halbton zu Des (wie bei der Modulation von c-moll nach As-Dur, das zeigt auch die Notenbezeichnung) und B um ein syntonisches Komma.

Modulation in Richtung Dominante

Faustregel: Der 2. und der 7. Ton der Zieltonart ändern sich.

Beispiel: Modulation von C-Dur über E-moll nach G-Dur

C-Dur

Name des Tones		C		D		E		F		G		A		H		c
Frequenz		264		297		330		352		396		440		495		528
Frequenzverhältnis			9/8		10/9		16/15		9/8		10/9		9/8		16/15

Die Akkorde der Tonika C-E-G, der Subdominante F-A-c und der Dominante G-H-d sind rein.

E-moll Zum besseren Vergleich nicht in der Reihenfolge E-FIS-G-A-H-c-d-e sondern C-D-E-FIS-G-A-H-c.

Name des Tones		C		D		E		FIS(!)		G		A		H		c
Frequenz		264		297		330		371,3(!)		396		440		495		528
Frequenzverhältnis			9/8		10/9		9/8		16/15		10/9		9/8		16/15

Hier sind die Akkorde der Tonika E-G-H, der Subdominante A-c-e und der Dominante (in moll) H-d-fis rein.

G-dur

Name des Tones		C		D		E		FIS(!)		G		A(!)		H		c
Frequenz		264		297		330		371,3(!)		396		445,5		495		528
Frequenzverhältnis			9/8		10/9		9/8		16/15		9/8		10/9		16/15

Hier sind die Akkorde der Tonika G-H-d, der Subdominante C-E-G und der Dominante D-Fis-A rein.

Im Vergleich zu C-Dur hat sich bei G-Dur das das F um einen Halbton zu FIS erhöht - wie bei der Modulation von C-Dur nach e-moll - (das zeigt auch die Notenbezeichnung), aber auch das A um ein syntonisches Komma (Frequenzverhältnis ⁸¹/₈₀$\widehat{=}$21,5 Cent) geändert. Sonst bestünde die Dominante in G-Dur D-FIS-A bzw. in E-moll H-d-fis nicht mehr aus reinen Terzen und Quinten.

Hörbeispiel

Modulation C-Dur nach G-Dur	Nur Sopran	Die reine Terz im Sopran des Akkords - wie hier im zweiten und letzten Akkord - erscheint dem an die gleichstufige Stimmung gewöhnten Ohr als zu tief intoniert. Der klare Klang dagegen überzeugt: Die Wirkung der Modulation als Steigerung und Aufhellung verblasst etwas in der gleichstufigen Stimmung. Zum Vergleich: Anhören gleichstufig?/i
Anhören rein?/i	Anhören rein?/i

Beispiel: Modulation von c-moll nach g-Moll

Hier erhöht sich F um ein syntonisches Komma (wie bei der Modulation von c-moll nach Es-Dur) und As um einen Halbton zu A (das zeigt auch die Notenbezeichnung).

Vergleich der erweiterten reinen Stimmung mit der gleichstufigen Stimmung

Nimmt man zu den Tönen der Dur- und Molltonleiter das FIS von G-Dur und das DES von f-moll dazu, erhält man die 12-stufige chromatische Skala der reinen Stimmung.

Chromatische Skala der reinen Stimmung von C-Dur und C-moll ergänzt um FIS und DES:

Hinweis: Beim Vergleich von Intervallen verwendet man die Einheit Cent. Dabei gilt: 1 Oktave = 1200 Cent.

Name des Tones	C	DES	D	ES	E	F	FIS	G	AS	A	B	H	c
Frequenz	264	281,6	297	316,8	330	352	371,25	396	422,4	440	475,2	495	528
In Cent	0	112	204	316	386	498	590	702	814	884	1018	1088	1200

Folgende Dreiklänge enthalten reine Quinten und reine kleine und große Terzen.

In dieser Stimmung kann man nur C-Dur und c-moll sowie As-Dur und e-moll (mit Molldominante H-D-Fis) rein spielen. (Wird das Dis im Dur-Dominantakkord H-Dis-Fis von e-moll durch seine enharmonische Verwechslung ersetzt, so erhält man ein Es, das um 41 Cent zu hoch ist.) Um in allen Tonarten spielen zu können, werden bei der gleichstufigen Stimmung die Halbtöne angepasst. Dass hierbei kein Dreiklang mehr rein erklingt, wird als Kompromiss akzeptiert.

Chromatische Skala der gleichstufigen Stimmung:

Name des Tones	C	CIS/DES	D	DIS/ES	E	F	FIS/GES	G	GIS/AS	A	AIS/B	H	c
Frequenz	261,6	277,2	293,7	311,1	329,6	349,2	370	392	415,3	440	466,2	493,9	523,3
In Cent	0	100	200	300	400	500	600	700	800	900	1000	1100	1200

Die gleichstufige Stimmung erhält man auch, indem man das pythagoreische Komma im Quintenzirkel F-C-G-D-A-E-H-Fis-Cis-Gis-Dis-Ais-Eis-His=(C?) auf die zwölf Quinten verteilt. Die reine Quinte (702 Cent) unterscheidet sich von der gleichstufigen (700 Cent) nur geringfügig. Die große Terz (386 Cent) wird bei der gleichstufigen Stimmung (400 Cent) immerhin um 14 Cent "geschärft".

Tabelle der Frequenzverhältnisse der erweiterten Tonleiter

Nimmt man zur C-Dur- und c-Moll-Tonleiter noch das Fis von G-Dur (dominantisch) und das Des von f-Moll (subdominantisch) hinzu, erhält man die 12-stufige chromatische Tonleiter.

C-Dur/c-moll chromatisch		C		Des		D		Es		E		F		Fis		G		As		A		B		H		c
Frequenzverhältnis zum Grundton		1/1		16/15		9/8		6/5		5/4		4/3		45/32		3/2		8/5		5/3		9/5   (16/9)		15/8		2/1
Frequenzverhältnis benachbarter Töne			16/15		135/128		16/15		25/24		16/15		135/128		16/15		16/15		25/24		27/25   (16/15)		25/24   (135/128)		16/15
in Cent			112		92		112		71		112		92		112		112		71		133 (112)		71 (92)		112

Hier ist das B als reine kleine Terz zu G gewählt (zu c-Moll gehörig). In manchen (quintenbetonten) Darstellungen wird das B als Quarte zu F gewählt werden (Angabe in Klammer) mit dem Vorteil, dass das Intervall AB ein diatonischer Halbton ist. Dann gehört dieses B aber schon zu F-Dur.

Wie man feststellen kann, ist ein in dieser Stimmung gestimmtes Instrument nur für C-Dur und c-moll (bei geeignetem B) sowie As-Dur und e-moll brauchbar und wird praktisch nicht realisiert.

Siehe auch: ausführliche Tabelle der Intervalle der reinen Stimmung

Kleiner und großer Halbton

→ Hauptartikel: Halbton

Bei der reinen Stimmung gibt es den großen, den diatonischen Halbton mit dem Frequenzverhältnis $\frac{16}{15} \widehat{\approx}\ \text {112 Cent}$ und die kleinen, die chromatischen Halbtöne mit den Frequenzverhältnissen $\frac{135}{128} \widehat{\approx}\ \text {92 Cent}$ und $\frac{25}{24} \widehat{\approx}\ \text {71 Cent}$

In der chromatisch erweiterten C-Dur/c-moll-Tonleiter:

Diatonische Halbtöne mit 112 Cent: E→F und H→c, sowie C→Des, Cis→D, D→Es und Dis→E.

Chromatische Halbtöne mit 92 Cent: C→Cis sowie Des→D.

Chromatische Halbtöne mit 71 Cent: D→Dis sowie Es→E.

(Beachte: C→D ist ein großer Ganzton mit 204 Cent und D→E ein kleiner Ganzton mit 182 Cent. Daher unterscheiden sich die zwei chromatischen Halbtöne um 21 Cent.)

Mathematische Beschreibung

Siehe: Hauptartikel Tonstruktur (mathematische_Beschreibung) Die reine Stimmung.

Der Intervallraum der reinen Stimmung ist das Quint-Terz-System $\mathcal Q \mathcal T = \{n \cdot Ok + m \cdot Q +k \cdot T\|n,m,k \in \Z\}$.

Alle Intervall lassen sich als Vielfache der drei Grundintervalle Ok (Oktave), Q (Quint) und T (große Terz) darstellen.

Intervall	Darstellung	Frequenzverhältnis
Oktave	Ok (Grundintervall)	2:1
Quinte	Q (Grundintervall)	3:2
Große Terz	T (Grundintervall)	5:4
Quarte	Ok - Q	4:3
Kleine Sext	Ok - T	8:5
Kleine Terz	Q - T	6:5
Große Sext	Ok + T - Q	5:3
(Großer) Ganzton	Q + Q - Ok	9:8
Kleiner Ganzton	T - (Großer Ganzton) = Ok + T - Q - Q	10:9
Kleine Septime (1. Möglichkeit)	Ok - (Großer Ganzton) = 2Ok - 2Q	16:9
Kleine Septime (2. Möglichkeit)	Ok - (Kleiner Ganzton) = Q + Q - T	9:5
Halbton	Quarte - T = Ok - Q - T	16:15
Große Septime	Ok - Halbton = Q + T	15:8
Syntonisches Komma	2(Große Ganztöne) - T = 4Q - 2Ok - T	81:80
ausführliche Tabelle

Historische Entwicklung

Das Quint-Terz-Schema

Die Einführung der reinen Großterz (mit dem Saitenlängenverhältnis zwischen unterem und oberem Ton von 5:4) – als Ersatz und Vereinfachung des pythagoreischen Ditonus (81:64) – geht zurück auf die enharmonische Tetrachordteilung Didymos' (etwa 100 Jahre nach Pythagoras).

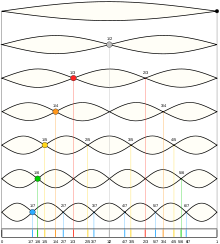
In der abendländischen Musik wurde die reine Großterz emanzipiert, indem sie zusammen mit der Sexte (8:5) im 15. Jahrhundert nicht mehr als Dissonanz, sondern als zunächst noch unvollkommene Konsonanz aufgefasst wurde und vor allem als Bestandteil des Dreiklanges zunehmend an musikalischer Bedeutung gewann. Die Deutung der Großterz als 5. Oberton in der Natur- bzw. Teiltonreihe sowie des Durdreiklanges als Zusammenklang von 4., 5. und 6. Oberton ist dabei eine (umstrittene) Definition der Neuzeit.

   C-Dur Akkord in der Obertonreihe^?/i

Wie jedes Tonsystem basiert auch das harmonisch-reine auf Intervallen, die als gegeben betrachtet werden. Das sind hier die Oktave ²/₁, Quinte ³/₂ und Terz ⁵/₄. Die anderen Intervalle das Tonsystems lassen sich so als Vielfache dieser Intervalle darstellen.

Wie schon bei den Beispielen mit Modulationen angedeutet wurde, ergibt sich aus der Vielzahl von Kombination dieser Intervalle ein (theoretisch) unendlicher Tonraum. Dieser Tonraum wird häufig mittels eines Tonnetzes wie folgt grafisch dargestellt:

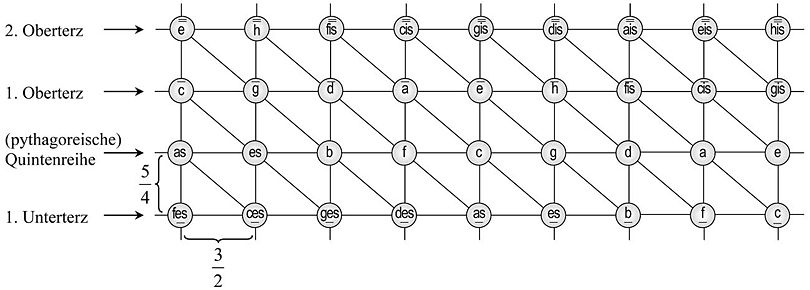
Darstellung im Tonnetz

Inspiriert von der pythagoreischen Stimmung, die auf der Kette von reinen Quinten basiert, hat sich in der Literatur seit Leonhard Euler die Darstellung des folgenden Beziehungsgeflechtes lange Zeit gehalten. Da die reine Terz nicht mit Quinten darstellbar war, mussten immer neue Quintenreihen betrachtet werden. (Alternativ dazu kann man die Veränderung der diatonischen Tonleitern bei Modulationen - wie oben - untersuchen.)

Diese grafische Darstellung des Quint-Terz-Schemas versteht sich als Beziehungsgeflecht von Tonigkeiten ohne fixierte Oktavlage (auch: „Chroma“, „Toncharakter“ ^[2]; engl.: „pitch class“), so dass zur Berechnung konkreter Intervallverhätnisse noch das entsprechende Vielfache der Oktave ²/₁ hinzu- oder weggenommen werden muss. Etwa bis zur Mitte des 19. Jahrhunderts galten die Oktave, die reine Quinte und Terz, sowie sämtliche Intervalle, die aus deren Kombination resultieren, als von der jeweiligen Stimmung unabhängiges, eigentlich „gemeintes“ Tonsystem der Dur-/Moll-tonalen Musik und das „Tonnetz“ als entsprechende Abbildung dieser Tonbeziehungen. Durch die zunehmende Alterations-Harmonik, enharmonische Verwechslungen und Ganztonskalen ist eine solche Trennung von „gedachtem System“ und „realisierbarer Stimmung“ (spätestens) ab der Spätromantik nicht mehr gegeben, da derartige Phänomene nicht nur pragmatisch, sondern auch (musik-)theoretisch die gleichschwebende Temperatur voraussetzen.

Das eigentliche „Tonnetz“ wurde 1773 von Leonhard Euler als speculum musicum („Abbild der Musik“) in seiner gleichnamigen Schrift „De harmoniae veris principiis per speculum musicum repraesentatis“ ^[3] vorgestellt, und von da an – zusammen mit den von Moritz Hauptmann ^[4] eingeführten „Kommastrichen“ a, e, h und des, as, es, usw. – von zahlreichen Theoretikern zu verschiedenen Zwecken abgewandelt (u. a. von Hermann v. Helmholtz ^[5], Arthur v. Oettingen ^[6] und Hugo Riemann ^[7]). Die unterschiedlichen Charaktere von Tönen gleichen Namens aber verschiedener Lage im (unendlichen) Tonraum ergibt sich in harmonisch-reiner Stimmung nicht nur aus einer jeweils anderen Tonumgebung und Harmonisierung (etwa das e im C-dur-Akkord c-e-g und das e im E-dur-Akkord e-gis-h), sondern auch aus einem (minimalem) Tonhöhenunterschied zwischen den jeweiligen Tonstufen (e und e):

Über c liegt seine Terz ⁵/₄ e. In der Quintenreihe von c liegt aber auch ein e; als 4. Oberquinte von c kommt ihm das Tonverhältnis ⁸¹/₁₆ zu (3⁴/2⁴). Wird diese Oberquinte um 2 Oktaven nach unten verschoben, so dass sie bei ⁵/₄ e liegt, ergibt sich ihr Tonverhältnis zu c wie folgt:

$\tfrac{81}{16} \cdot \tfrac{1}{4} = \tfrac{81}{64}$

Vergleichen wir die beiden e miteinander,

$\tfrac{5}{4} : \tfrac{81}{64} = \tfrac{5}{4} \cdot \tfrac{64}{81} = \tfrac{5 \cdot 16}{81} = \tfrac{80}{81}$

zeigt sich, dass der Tonhöhenunterschied ⁸⁰/₈₁ beträgt. Er wird syntonisches Komma genannt.
Die 80 ist der Terz ⁵/₄ e zuzuordnen (⁵/₄ = ⁸⁰/₆₄), also ist ⁵/₄ e [um ca. 21,51 Cent, bzw. etwa einen Zehntel-Ton] tiefer als das gleichnamige ⁸¹/₆₄ e“ ^[8]

Umgekehrt liegt das as (etwa im f-Moll-Akkord f-as-c) ein syntonisches Komma über der gleichnamigen Tonstufe in der Quintenkette as-es-b-f-c:

$\tfrac{4}{5} : \tfrac{64}{81} = \tfrac{4}{5} \cdot \tfrac{81}{64} = \tfrac{81}{5 \cdot 16} = \tfrac{81}{80}$

Die C-Dur-Tonleiter in harmonisch-reiner Quint-Terz Stimmung

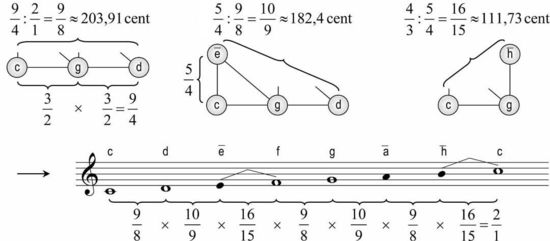
Die reine C-Dur-Tonleiter kann verstanden werden als Auswahl derjenigen sieben Tonstufen aus dem Quint-Terz-Schema, die zur Intonation der drei Hauptfunktionen Subdominante (S), Tonika (T) und Dominante (D) – also für die „authentische“ Kadenz benötigt werden:

   C-Dur-Tonalität^?/i

Die eigentliche Skala entsteht durch Transposition dieser Tonstufen in die entsprechende Oktavlage – beispielsweise zwischen c¹ und c². Sie besteht nun – im Gegensatz zur pythagoreischen Skala – nicht mehr aus zwei, sondern aus drei Intervallschritten verschiedener Größe, dem großen Ganzton ⁹/₈, dem kleinen Ganzton ¹⁰/₉ und dem diatonischen Halbton ¹⁶/₁₅ :

   reine C-Dur-Tonleiter^?/i

Diese siebenstufige Tonleiter erlaubt nun zwar die harmonisch-reine Intonation der Hauptfunktionen T, S und D, doch wirkt sie melodisch unsauber, da die jeweiligen Terzen e, a und h in melodischen Zusammenhang als zu niedrig empfunden werden können. Insbesondere der Leitton h-c ist mit seinen 111,73 Cent problematisch, da er der Tendenz widerspricht, die Strebewirkung von Leittönen durch eine möglichst enge Intonation zu erhöhen (beispielsweise durch das pythagoreische Limma h-c ²⁵⁶/₂₄₃ zu 90,22 Cent). Viele der Intonationsschwierigkeiten – etwa von Streichern, die häufig geschärfte Terzen bzw. Leittöne spielen, und Bläsern – lassen sich auf die Unvereinbarkeit von harmonischer und quasi pythagoreisch-melodischer Reinheit zurückführen.^[9].

„In didymischer Auffassung ist cis tiefer als des, gis tiefer als as, dis tiefer als es, usw. Eine Bewertung, die dem melodischen Schrittempfinden des instinktiven Musikers durchaus widerspricht! Und in der Tat ist die naturgewollte primäre Terz gar kein melodisches, sondern ein harmonisches Intervall. […] Die griechische, mathematisch orientierte Musiktheorie zählte die pythagoreische Terz den Dissonanzen zu. Sie hatte in dem Sinne recht, als der Begriff der Konsonanz und Dissonanz ja durchaus eine harmonische Wertung ist. […] Die Linearität der Melodie hat nichts mit großen und kleinen Ganztönen, mit Kommadifferenzen und dergleichen zu schaffen.“ − Sigfrid Karg-Elert  ^[10]

Die zwei verschieden großen Ganztöne ⁹/₈ und ¹⁰/₉ – die Auslöser dieses „Konflikts“ – ergeben sich (zwangsläufig) aus der arithmetischen Teilung der (reinen) Großterz ⁵/₄. Deren Differenz entspricht dem sog. syntonischen oder didymischem Komma ⁸¹/₈₀ mit ca. 21,51 Cent; d. h. die Tonstufen, die in der Reihe über den (gleichnamigen) Tonstufen im Tonnetz liegen, werden etwa einen Zehntel-Ton tiefer als diese intoniert (e:e = 80:81). Eine Lösung dieses zusätzlichen Problems liefert die mitteltönige Stimmung mit der geometrischen Teilung der Großterz, was zu zwei gleichgroßen Ganztönen (jeweils 193,156 Cent) führt, ohne die Reinheit der Terz in Frage zu stellen.

Die „zweierlei d in C-Dur“

Siehe Modulation in Richtung Subdominante. Dort wird erläutert, dass der Akkord auf der II. Stufe als Beginn einer Modulation gesehen werden muss.

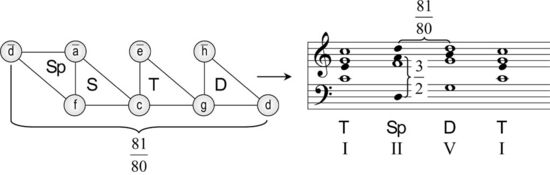
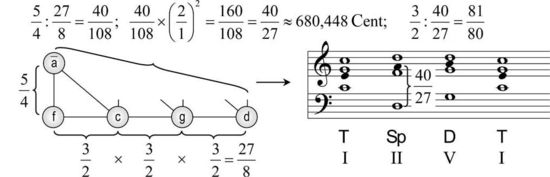
Ein anderes Problem besteht in der Intonation der Quinte d-a, die 680,448 Cent um ein syntonisches Komma zu eng, und damit dissonant, erscheint. Sie erklingt u. a. im d-Moll-Akkord (d-f-a) auf der zweiten Stufe bzw. in der Kadenz mit Subdominantparallele (T-Sp-D-T):

   dissonantes d-Moll in C-Dur^?/i

Die Bereinigung dieses dissonanten Intervalls erfordert eine zusätzliche Tonstufe d (d:a= 2:3 statt d:a = 27:40), wodurch allerdings das syntonische Komma ⁸¹/₈₀ zu einem musikalisch relevanten (hörbaren) Intervallschritt wird.

   zweierlei d in C-Dur^?/i

Abgrenzung

Obertonpositionen

Nicht nur in der abendländischen Musiktradition, auch in außereuropäischen Musikkulturen trifft man auf den Begriff der „reinen Stimmung“, wenn harmonisch-rein intoniert wird. In Einzelfällen können auch weitere Intervalle der Obertonreihe einbezogen werden wie etwa die Naturseptime (7. Teilton) oder das Alphorn-Fa (11. Teilton).

Klangbeispiel: Vergleich reine, mitteltönige und gleichstufige Stimmung

Anhören
Reine Stimmung	Reine Stimmung langsam	1/4-Komma-Mitteltönige Stimmung	gleichsrufige Stimmung
1. Zeile?/i 2. Zeile?/i	1. Zeile?/i 2. Zeile ?/i	1. Zeile?/i 2. Zeile?/i	1. Zeile?/i 2. Zeile?/i

Hier sind in reiner Stimmung in g-Moll die Kadenzakkorde G-B-D, C-Es-G und D-Fis-A rein. Bei der Modulation zu B-Dur mit den reinen Kadenzakkorden B-D-F, Es-G-B und F-A-C erhöht sich der Ton C um ein syntonisches Komma.

weitere Klangbeispiele

Für die klangliche Darstellung reiner Stimmungen wurde ein bekanntes, freilich historisch nicht korrektes Beispiel gewählt, das es möglich macht, die diffizilen Unterschiede deutlich zu hören. Es wurde von Johann Sebastian Bach für eine der (vielen) wohltemperierten Stimmungen konzipiert; für welche genau lässt sich heute nicht mehr mit Sicherheit rekonstruieren.

Johann Sebastian Bach: Präludium in C-Dur aus dem ersten Band des Wohltemperierten Klaviers, BWV 846

Beispiel 1: Takte 1 bis 5

• Die im Text beschriebene 7stufige (reine) C-Dur-Tonleiter führt zwar zu einem melodisch sinnvollen großen Ganzton (⁹/₈) c-d [bei a)], doch wird die Quinte d-a [bei b)] dadurch unrein (⁴⁰/₂₇ statt ³/₂, sie ist mit ca. 680,448 Cent um ein syntonisches Komma zu klein). Anhören^?/i

• Durch Erweiterung der Skala um ein erniedrigtes d [bei a)] wird die Quinte d-a [bei b)] nun zwar bereinigt, doch entsteht zum einen ein unmelodischer kleiner Ganzton (¹⁰/₉) und zum anderen eine deutlich hörbare (syntonische) Kommadifferenz (⁸¹/₈₀) zwischen den d's des zweiten und des dritten Taktes [bei c)]. Anhören^?/i

• Bei Annahme der Naturseptime (⁷/₄ statt ⁹/₅) im Dominantseptakkord [bei d)] entsteht ein zusätzliches „septimales Komma“ (⁶⁴/₆₃, ca. 27,264 Cent) zwischen dem f des zweiten und des dritten Taktes [bei e)]. Der Gleitton f-e wird als „septimaler Halbton“ (²¹/₂₀, ca. 84,467 Cent) eng intoniert [bei f)]. Anhören^?/i

Beispiel 2: Takte 5 bis 11

• Auch die 12stufige, chromatische Skala beinhaltet (nur) die unreine Quinte d-a (⁴⁰/₂₇), die hier zweimal als Teil des Doppeldominant-Septakkordes erklingt [bei a)]. Anhören^?/i

• Der Ausgleich dieser Quinte erfordert nun ein pythagoreisch eingestimmtes a (²⁷/₁₆ statt ⁵/₃), das gegenüber dem a als Grundton der Tonikaparallele um ein syntonisches Komma erhöht ist [bei b)]. Da die Kommadifferenzen hier in einer der Mittelstimmen erklingen fallen sie kaum ins Gewicht – mit einem durchaus annehmbaren klanglichen Resultat. Anhören^?/i

• Im Gegensatz dazu führt der als Naturseptime intonierte Ton c der Doppeldominante wiederum zum deutlich hörbaren „septimalen Komma“ [bei c)]. Anhören^?/i

Trivia

Arnold Schönberg beschreibt in seinem musiktheoretischen Werk Harmonielehre. (Wien, 1911; 3te Auflage 1922) die Reine Stimmung, wobei er dem Tritonus (Fis) die Oktavmitte (gleichschwebend) zuordnet.

Literatur

• Hermann von Helmholtz Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, Vieweg, Braunschweig 1863, Nachdruck: Minerva-Verlag, Frankfurt/Main 1981, ISBN 3-8102-0715-2 Auszug

• Ludwig Riemann Populäre Darstellung der Akustik in Beziehung zur Musik. Verlag Friedrich Vieweg, Braunschweig ebenfalls 1896.

• Bettina Gratzki: Die reine Intonation im Chorgesang. Verlag für systematische Musikwissenschaft GmbH Bonn 1993 (Exzerpt)

• Ross W. Duffin: How Equal Temperament Ruined Harmony (And Why You should Care) Verlag W.W.Norton&Company, New York · London, 2007 (Exzerpt)

• Albert Limbach: Die Kunst reiner Intonation. Studien zu unbegleitetem Chorgesang in Oper und Konzert. Wiesbaden 1980

Weblinks

• "Die reine Stimmung" von Joachim Mohr

Siehe auch

• Solmisation
• Tonic sol-fa, dort auch der Bericht von Hermann von Helmholtz, einem Verfechter der reinen Stimmung
• Mitteltönige Stimmung
• Wohltemperierte Stimmung
• Gleichstufige Stimmung
• Quintenzirkel

Quellen

1. ↑ Dies gilt auch für die Aufführungspraxis der Musik der Klassik und Romantik bei lang ausgehaltenen Akkorden. Eine Musik jedoch, die Leittöne bevorzugt (Romantik), weicht von der reinen Stimmung insofern ab, dass der Leitton die (tiefer gestimmte) Terz einer (Zwischen)Dominante ist. Beim "expressive" Leitton wird statt eines reinen Halbtons (112 Cent) ein Limma (90 Cent) oder ein noch engeres Intervall intoniert.
2. ↑ vgl.: Jacques Handschin: Der Toncharakter. Eine Einfuhrung in die Tonpsychologie; Zürich, 1948
3. ↑ Leonhard Euler: De harmoniae veris principiis per speculum musicum repraesentatis, veröffentlicht in Novi Commentarii academiae scientiarum Petropolitanae 18, St. Petersburg, 1774
4. ↑ Moritz Hauptmann: Die Natur der Harmonik und Metrik, Leipzig, 1853
5. ↑ Hermann v. Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, Braunschweig, 1863
6. ↑ Arthur von Oettingen: Harmoniesystem in dualer Entwicklung. Studien zur Theorie der Musik, Dorpat u. Leipzig, 1866; überarbeitete zweite Auflage als Das duale Harmoniesystem, Leipzig, 1913
7. ↑ z.B.: Hugo Riemann: Ideen zu einer „Lehre von den Tonvorstellungen“, in: Jahrbuch Peters 21/22, 1914/15
8. ↑ Martin Vogel: Die Lehre von den Tonbeziehungen, Bonn – Bad Godesberg, 1975, S. 103f
9. ↑ Ross W. Duffin ("How Equal Temperament Ruined Harmony (And Why You should Care)" Verlag W.W.Norton&Company, New York · London, 2007) belegt allerdings, dass diese "Expressive Intonation", d.h. die Verwendung von geschärften Leittönen, vor allem seit Pablo Casals (1876-1973) eine durchaus moderne Erscheinung ist. Hermann von Helmholtz, der das Spiel von Joseph Joachim physikalisch untersuchte, stellt fest, dass Joachim die Terzen (fast) rein intonierte, was sich auch in seinen Schallplattenaufnahmen von 1903 - trotz technischer Mängel - bestätigt.
10. ↑ Sigfrid Karg-Elert: Polaristische Klang- und Tonalitätslehre. Leipzig, 1930, S. 6f

Stimmungen des abendländischen zwölfstufigen Tonsystems

Aulos-Modi | Gleichstufige Stimmung | Kirnberger-Stimmung | Mitteltönige Stimmung | Pythagoreische Stimmung | Reine Stimmung | Silbermann-Sorge-Temperatur | Vallotti-Stimmung | Werckmeister-Stimmung | Wohltemperierte Stimmung