Bahnstörung

Bahnstörungen sind Abweichungen der tatsächlichen Flugbahn eines Himmelskörpers von der nach einem Modell berechneten theoretischen Flugbahn.

Was unter einer Bahnstörung zu verstehen ist, hängt vom Detaillierungsgrad des zugrundeliegenden Modells ab, und von den darin enthaltenen Vereinfachungen.

Das Modell der Flugbahn

Erstes keplersches Gesetz

Die mathematische Grundlage für die Darstellung einer Flugbahn eines Himmelskörpers wurde durch Johannes Kepler geschaffen und nach ihm als keplersches Gesetz benannt. Diese Theorie konnte später durch das Newton'sche Gravitationsgesetz von Isaac Newton bestätigt werden. Die Beschreibung der Abhängigkeiten der Himmelskörper, zum einen der Flugbahn (auch als Trajektorie bezeichnet) und zum anderen die Kräfteeinwirkung von zwei Massekörpern, erfolgt bei diesen zwei Modellen unter der Annahme von Vereinfachungen. Streng genommen ist das keplersche Gesetz ein Zweikörperproblem, da mit diesem Modell lediglich die Flugbahn eines Himmelskörpers um eine Zentralmasse, z. B. Erde und Sonne, beschrieben wird. Beim Newtonschen Gesetz wird eine Vereinfachung durch die Betrachtung der Himmelskörper als Punktmassen erreicht.

In der Realität ist der Raum (der Weltraum), in dem die Flugbahnen der zu beschreibenden Himmelskörper verlaufen, „nicht leer“ und die Objekte können auch nicht als Punktmasse betrachtet werden. Vielmehr ist dieser Raum mit unterschiedlichen, zeitlich veränderlichen Massendichten und elektrischen Ladungsdichten gefüllt. Objekte in diesem Raum können sich über Gravitationsfelder, elektrische Felder, Magnetfelder oder Materieströme gegenseitig beeinflussen. Bei Betrachtung der Gravitation wird hierbei das Zweikörperproblem zu einem Mehrkörperproblem und die Betrachtung weiterer bisher vernachlässigter Krafteinflüsse (Strahlungsdruck, Luftwiderstand, u. ä.) gewinnt an Bedeutung. Bahnstörungen ergeben sich demzufolge aus der Vereinfachung des zugrunde liegenden mathematischen Modells zur Beschreibung von Flugbahnen der Himmelskörpern in Bezug zu den in der Realität existierenden Bedingungen.

Arten von Bahnstörungen

Bahnstörungen entstehen durch äußere Krafteinwirkung auf ein Objekt im Weltraum. Dies führt zu einer Abweichung der Flugbahn des Objektes, das nach dem vereinfachten keplerschen Modell beschrieben werden kann. Die Ursachen können hervorgerufen werden durch:

• Heterogenes Gravitationsfeld der Zentralmasse
• Gravitationskräfte anderer Himmelskörper
• Materieansammlung (Nebel, Atmosphären, …)
• Strahlungsdruck
• Magnetfelder und Ionenflüsse
• Relativistische Effekte

Gravitative Kräfte

Zur besseren Visualisierung der gravitativen Störungen wird im Nachfolgenden der erdnahe Raum näher betrachtet. Diese Störungen können in drei Rubriken unterteilt werden. Zum einen das Störpotential aus der Masseverteilung der Erde (bzw. der Zentralmasse), zum anderen das Störpotential aus den gravitativen Kräften anderer Himmelskörper auf das Erdgravitationsfeld (bzw. auf das Gravitationsfeld der Zentralmasse) und zum Schluss der direkte gravitative Einfluss der anderen Himmelskörper auf ein Objekt in der Erdumlaufbahn.

Die Erde als Geoid

Erdschwerefeld, Abweichungen stark überhöht

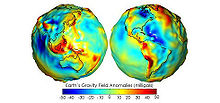
Das Newton´sche Modell betrachtet die Erde als Punktmasse, diese Vereinfachung ist nicht korrekt. In erster Näherung kann die Erde als ein abgeplatteter Rotationsellipsoid gesehen werden, was bedeutet, dass aufgrund der Erdrotation und der daraus resultierenden Zentrifugalkraft die Materie in Äquatornähe weiter nach außen gedrückt wird (Erdabplattung). Der Radius der Erde ist deshalb am Äquator größer als an den Polen. Weiterhin ist die Dichte der Erde nicht homogen. Zum einen ist die Dichteverteilung im Erdmantel, aufgrund von Strömungs- und Thermalschwankungen (siehe z. B. Mantelkonvektion), nicht einheitlich. Und zum anderen ist die Verteilung der Masse in der Lithosphäre sehr unterschiedlich. Auf der Erde existieren größere Land- und Wasserflächen. Die Landflächen besitzen, im Gegensatz zu den Ozeanen größere Massedichten, da hier u. a. Metalle und Schwermetalle anzutreffen sind. Dies führt zu dem Effekt, dass aus Sicht der Massedichtenverteilung die Erde aussieht wie eine Kartoffel (Geoid). Diese unterschiedliche Verteilung führt zu regional unterschiedlichen Gravitationspotentialen die auf ein Objekt im Erdorbit einwirken. Neue Erkenntnisse lieferten hier die Missionen CHAMP, GRACE und GOCE.

Die Gezeiten

Schematische Darstellung der Gezeitenkräfte und Flutberge

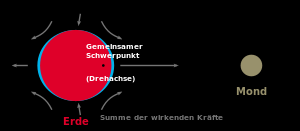
Die Auswirkung anderer Himmelskörper auf die Erde, wie Sonne und Mond, sind durch die Gezeiten sichtbar. Diese können in drei Arten unterschieden werden: Erdgezeiten, Ozeangezeiten und Atmosphärengezeiten. Die Gezeiten beeinflussen die Massedichtenverteilung auf der Erde und beeinflussen somit wieder das Gravitationspotential regional. Neben der gravitativen Auswirkung spielt auch die Ausdehnung der Atmosphäre eine weitere Rolle (siehe nicht-gravitative Kräfte).

Der direkte Einfluss anderer Himmelskörper

Der dritte gravitative Einfluss entsteht direkt durch die Krafteinwirkung anderer Himmelskörper auf ein Objekt in der Erdumlaufbahn. Der Einfluss hängt von den Orbitparametern ab. So spielen Mond und Sonne eine wesentliche Rolle, aber auch die Venus und der Jupiter besitzen einen kleinen Einfluss. Dieser Einfluss ist im Bereich der geostationären Satelliten (GEO) größer als bei den Satelliten in den unteren Erdumlaufbahnen (LEO und MEO). Neben den direkten Einfluss eines Himmelskörpers durch dessen Gravitationsfeld existiert noch ein indirekter Einfluss, der auf die Interaktion der Gravitationsfelder von Massen zurückzuführen ist. Durch diese Interaktion entstehen Gravitationswellen, die den Raum stauchen und dehnen. Diese Art der Störung könnte bisher nur indirekt nachgewiesen werden, da die Auswirkung minimal ist und deshalb bisher noch nicht experimentell nachgewiesen werden konnte.

Nicht-gravitative Kräfte

Durchschnittlicher Luftdruck und Luftdichte in Abhängigkeit von der Höhe

Sonnensegel (Entwurf)

Die Magnetosphäre der Erde

Der Strömungswiderstand

Die erste bedeutende Art von nicht-gravitativen Bahnstörungen ist der Strömungs- oder Luftwiderstand eines sich bewegenden Objektes durch ein Fluid der eine Abbremsung dieses Objektes bewirkt. Die Größe der Krafteinwirkung hängt von der Dichte des Fluids, bzw. in den unteren Erdumlaufbahnen von der Luftdichte, der senkrecht zur Flugrichtung gegebenen Fläche des Objektes und der relativen Geschwindigkeit zwischen Fluid und bewegtem Objekt ab. Zur Beschreibung des Widerstands wurde der ballistische Faktor eingeführt. Ein präzise Berechnung des Widerstandes in der oberen Erdatmosphäre ist nur durch die Berücksichtigung der Gezeiteneinwirkung und der Atmosphärenaufheizung aufgrund der Tag-Nacht-Seite, durch derer sich die Atmosphäre unterschiedlich ausdehnt, möglich. Für erste Überschlagsrechnungen kann die barometrische Höhenformel verwendet werden.

Der Strahlungsdruck

Neben dem Luftwiderstand existiert, als weitere mögliche Bahnstörung, der Strahlungsdruck. Bei diesem Effekt wird der Impuls eines Photons bei Absorption oder Emission (bzw. Reflexion) dieses Teilchens (siehe Welle-Teilchen-Dualismus) auf ein Objekt übertragen. Im erdnahen Raum wird diese Krafteinwirkung durch die Sonnenstrahlung oder dem reflektierten Sonnenlicht von der Erde (Albedo-Strahlung) generiert. Eine Anwendung findet dieser Effekt im Bereich der Raumfahrtantriebe: als Solarsegel.

Die elektromagnetische Wechselwirkung

Für ionisierte oder magnetische Objekte spielt die elektromagnetische Wechselwirkung eine besondere Rolle. Neben den Himmelskörpern, wie Erde, Jupiter, Saturn, … die ein planetares Magnetfeld die Magnetosphäre besitzen, existiert durch die Sonne ein interplanetares Magnetfeld das durch den Sonnenwind verstärkt wird. Aufgrund der Wechselwirkung zwischen den Magnetfeldern oder dem Magnetfeld und den elektrischen Ladungen der Objekte wirkt eine weitere Kraft die eine Bahnstörung hervorrufen kann. Eine Anwendung findet dieser Effekt im Bereich der Raumfahrtantriebe: als Mini-Magnetospheric Plasma Propulsion (M2P2).

Kollisionen

Auch eine Kollision von zwei Himmelskörpern führt zu Bahnstörungen dieser beiden Objekte. Im erdnahen Raum ist das Ausmaß der Bahnstörung eines Objektes, im Gegensatz zu dem anzurichtenden Schaden (siehe z. B. Satellitenkollision), eher gering. Eine besondere Rolle nimmt hierbei der Weltraummüll ein. Mit dem zunehmenden Weltraummüll und den Einsatz von passiven Schutzsystemen (Meteoriten und Fremdkörper Schutzschild, engl.: Meteoroids and Debris Protection System, MDPS) könnten derartige Einflüsse, Bahnstörungen von Satelliten aufgrund von Kollisionen, eventuell an Bedeutung gewinnen. Im Sonnensystem oder im Universum spielen Kollisionen eine wesentlich bedeutendere Rolle als im erdnahen Raum. Ob Einschläge, Sternenkollisionen oder Galaxiekollisionen, die theoretischen Bahnen der aufeinander stoßenden Objekte können sich hierdurch extrem verändern. So ist eine Theorie bzgl. der Entstehung des Mondes auf eine Kollision zwischen der Proto-Erde mit einem anderen Himmelskörper zurückzuführen. Durch diese „Verschmelzung“ wird aus zwei Objekten mit zwei theoretischen Flugbahnen ein Objekt mit einer neuen theoretischen Flugbahn.

Relativistische Kräfte

Vollständige Schwarzschildsche Lösung – Gravitationsfeld eines nicht-rotierenden Objektes

Die Zeitdilatation

Die relativistischen Effekte ergeben sich aus der Raum-Zeit-Krümmung des umgebenden Raumes eines bewegten Objektes im Bezug zu anderen Objekten. Zum einen muss die relativistische Zeitdilatation beachtet werden. Die Zeitdilatation kann zwar nicht als direkte Bahnstörung im eigentlichen Sinn gesehen werden, jedoch besitzt diese eine Auswirkung auf die technische Anwendung, so dass dieser Effekt in diesem Zusammenhang erwähnt wird. Die Zeitdilatation tritt zutage, da die Zeit keine absolute Größe ist, sondern von den Koordinatensystemen und deren Relation zueinander abhängt. In einem bewegten System vergeht die Zeit langsamer als in einem nicht bewegten System. In der technischen Anwendung hat dies zur Folge, dass zur Positionsbestimmung mittels eines GPS-Systems mindestens vier Satelliten benötigt werden, um diesen relativistischen Effekt ausgleichen zu können.

Die Raumkrümmung

Ein zweiter Effekt, ergibt sich aus der Raumkrümmung der zu Abweichungen der Beschleunigungen am Satelliten führt, gegenüber einen nicht gekrümmten Raum. Dies bedeutet, dass Objekte im Orbit um eine Zentralmasse betroffen sind, die den Raum krümmt. Die Berechnung der Korrekturen zu den Beschleunigungen erfolgt mittels der Schwarzschild-Metrik. Dieser Effekt konnte bei der Periheldrehung von Merkur nachgewiesen werden, bei dem nicht nur die Einflüsse der Planeten des Sonnensystems, sondern auch der relativistische Effekt eine Rolle spielen.

Der Lense-Thirring-Effekt

Der dritte relativistische Effekt ist der Lense-Thirring-Effekt, der eine Präzessionsänderung eines rotierenden Satelliten bewirkt, aufgrund der Verdrillung der Raumzeit. Die Satellitenmission Gravity Probe B bestätigte diesen Effekt.

Auswirkungen auf die Bahnelemente

Bahnelemente eines Himmelskörpers

Bahnstörungen können eingeteilt werden in:

• Säkulare Störung - die immer in gleicher Richtung (mathematisch monoton) wirken.
• Periodische Störung – die eine Regelmäßigkeit von Ereignissen aufweisen.
• Unregelmäßige Störungen und
• Zufällige Störungen

Die Wirkung von Bahnstörungen kann säkular (immer in gleicher Richtung) oder periodisch sein, sowie unregelmäßig in der Nähe irregulär geformter Himmelskörper oder in Materiewolken. Generell ändern sich die Zahlenwerte der jeweils sechs Bahnelemente (bzw. Satellitenbahnelemente) und können genähert mit dem Verfahren der Variation der Elemente berechnet werden. Dabei erhält (fast) jedes der Bahnelemente (a, e, i, Ω, ω, T) einen zeitabhängigen Term, die Bahnwinkel Ω, ω und der Zeitparameter T auch mehrere. Eine detaillierte Beschreibung der Berechnung muss aus den Quellen im Anhang entnommen werden.

Gravitative Kräfte

Änderung der Rektaszension und des Arguments des Perigäums aufgrund der Erdabplattung

Der Geoid

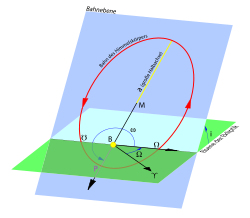
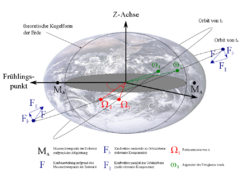
Auf die Bahnebene der Umlaufbahn eines erdnahen Satelliten übt das unregelmäßige Gravitationsfeld der Erde ein „Kippmoment“ aus, dem die Bahnebene durch eine Präzessionsbewegung nach den Kreiselgesetzen ausweicht. Diese Ausweichbewegung führt dazu, dass der aufsteigende Knoten bzw. die Knotenlinie nicht feststeht, sondern langsam in der Äquatorebene rotiert und sich damit die Rektaszension des aufsteigenden Knotens $\Omega\$ ständig ändert. Die Bahnebene dreht sich quasi um die z-Achse des astronomischen Koordinatensystems (Abb.: Bahnelemente 01, Bahnelemente 02). Gleichzeitig dreht sich die Apsidenlinie in der Bahnebene – ebenfalls durch Schwerkrafteinflüsse – um den Erdmittelpunkt. Damit erfährt auch das Argument des Perigäums $\omega\$ eine zeitliche Änderung. Diese zeitliche Änderung in Grad pro Tag (°/d) kann mit folgender Beziehung berechnet werden (siehe Satellitenbahnelement):

$\dot\Omega=-9{,}9641\cdot\left({\frac{{r_{A}}}{a}}\right)^{\frac{7}{2}}\cdot\frac{{\cos i}}{{\left({1-\varepsilon^2}\right)^2}}$.	(1)
$\dot\omega = 4{,}98\cdot\left({\frac{{r_{A}}}{a}}\right)^{\frac{7}{2}}\cdot\frac{{5\cos^2 i-1}}{{\left({1-\varepsilon^2}\right)^2}}$.	(2)

mit r_A als Erdradius.

Die Auswirkung dieser Bahnstörung kann auch positiv genutzt werden. Es kann durch entsprechende Auswahl der Inklination ein sonnensynchroner Orbit generiert oder das Perigäum über einen festen Erdpunkt gehalten werden. Dies kann wie folgt berechnet werden ^[1]:

$\dot \Omega = \frac{{360^\circ}}{{365\,\mathrm{Tage}}}$	$\quad\Rightarrow i = 96^\circ{-}99^\circ$
$\dot\omega = 0$	$\quad\Rightarrow i = 63{,}43^\circ$

Anmerkung: Eine weitere Auswirkung aufgrund der Inhomogenität der Erde ist die Ost-West-Drift. Diese wird aufgrund von Gravitationspotentialtälern und –bergen verursacht. Details sind der angegebenen Literatur zu entnehmen.

Auswirkungen anderer Himmelskörper

Gravitationskräfte durch Sonne und Mond

Wie zuvor schon erwähnt, können die Gravitationskräfte der anderen Planeten des Sonnensystems eine Periheldrehung eines Orbits verursachen (siehe Merkur). Für die Erdumlaufbahn gibt es jedoch zwei Himmelskörper, mit einem stärkeren Einfluss: Sonne und Mond.

Für geostationäre Satelliten sind diese Einflüsse von besonderer Bedeutung. In der nebenstehenden Abbildung sind die Kräfte aufgrund der Sonnen- und Mondgravitation eingezeichnet. Die Kraftvektoren können zerlegt werden in eine Komponente parallel und eine senkrecht zur Satellitenbahnebene (Seitenansicht). Die senkrechte Komponente ist eine säkulare und die parallele eine periodische Störung. Die säkulare Störung wirkt akkumulierend in eine Richtung und beeinflusst analog der Erdabplattung die Bahnelemente i, Ω und ω. Für GEO-Satelliten sind $\dot\Omega$ und $\dot\omega$ gleich Null, aufgrund von e = i = 0, so dass diese Störung lediglich eine Auswirkung auf die Inklination hat. Wird bei einem geostationären Satelliten diese Störung nicht korrigiert (z. B. durch eine entsprechende Bahnregelung), so wie dies beim Artemis Satelliten der Fall ist, erfährt dieser eine Nord-Süd-Drift von:

$\Delta i = 0{,}76^\circ/\text{Jahr}$

Die periodische Komponente (Abb. Draufsicht) ändert im Laufe der Zeit seine Richtung und auch seinen Wert. Eine Akkumulation über einen entsprechenden Zeitraum hat eine annähernde Kompensation der Krafteinwirkung zur Folge. Aufgrund des geringen Störungswertes und des Wechsels der Richtung werden die Bahnelemente langfristig nicht beeinflusst. Es können sich lediglich lokale Abweichungen ergeben.

Nicht-gravitative Kräfte

Auswirkung des Sonnenwindes auf einen Orbit

Der Sonnendruck

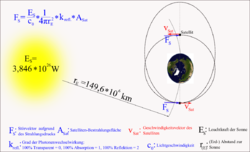
Der Strahlungsdruck der Sonne wird durch die Impulsübertragung der Photonen auf absorbierende und emittierende Flächen hervorgerufen. Diese Krafteinwirkung bewirkt eine kontinuierliche Beschleunigung die von der Sonne weg führt und so eine Änderung der Exzentrizität $\epsilon$ des Orbits hervorruft. Die Störgröße ist abhängig von der Größe der bestrahlten Fläche (u. a. der Solarpanel) und von dessen Reflexionsfaktor. Die Impulsübertragung des Photons erfolgt zum einem bei der Absorption und wird ein zweites Mal bei der Emission übertragen, das bedeutet, dass das Photon bei einer Reflexion maximal zwei Impulse übertragen kann. Eine Exentrizitätsänderung wird hervorgerufen (siehe Abb.), da das Objekt bei seiner Umkreisung des Zentralkörpers auf der einen Seite beschleunigt wird (Störgröße wirkt in Richtung des Flugvektors) und auf der anderen Seite gebremst wird (Störgröße wirkt entgegen der Richtung des Flugvektors). Da die Störgrößen in beiden Fällen gleich groß sind und sich demzufolge kompensieren, ändert sich die Energie des Orbits nicht, so dass die Umlaufzeit konstant bleibt. Der Sonnendruck p kann wie folgt berechnet werden:

$p = (1+r) \frac{S}{c} = 4{,}46 \cdot 10^{-5}\, \mathrm{N}/\mathrm{m}^2$

wobei S die Leuchtkraft der Sonne (in Erdnähe 1372 W/m²) und c die Lichtgeschwindigkeit darstellt. Der Reflexionsfaktor r besitzt einen Wert zwischen 0 und 1.

Weiterhin kann die Auswirkung des Sonnenwindes auch bei Kometenschweife und Materiewolken beobachtet werden. Darüber hinaus hindert der Sonnenwind die Teilchenströme der interstellaren Materie daran in das Sonnensystem einzudringen und erzeugt so die Heliosphäre.

Restatmosphäre

Bis zu einer Höhe von ungefähr 500 km ist die Restatmosphäre eine der stärksten Störgrößen. Diese wirkt in Flugrichtung, wobei die Fläche senkrecht zur Flugrichtung von Bedeutung ist. Die Störgröße (oder auch Strömungswiderstand unter freier Molekularströmung - siehe Knudsen-Zahl) führt zu einem Energieverlust der Orbitbahn des Objektes (siehe Vis-Viva-Gleichung – kinetische und potentielle Energie), was zur Folge hat, dass sich das Objekt auf einer Spiralbahn der Erde nähert und dort in der Erdatmosphäre verglüht. Die Störgröße berechnet sich zu:

$F_{D}= \frac{1}{2} c_{w} A \rho v^2$

wobei:

• C_D – ist der Widerstandsbeiwert für freie Molekularströmung und liegt zwischen 2,3 und 2,5^[2]
• A – Fläche senkrecht zu Flugrichtung
• ρ – Luftdichte in entsprechender Höhe
• v – Geschwindigkeit des Objektes

Um die Charakteristika von Objekte bei einem Wiedereintritt vergleichen zu können wurde der ballistische Faktor B eingeführt. Dieser gibt Auskunft über die Masse, Fläche und den Widerstandbeiwert und berechnet sich zu:

$B=c_{w}\frac{A}{m}$

Die Störgröße kann auch zu Gunsten einer Raumfahrtmission als Aerobraking Manöver eingesetzt werden.

Berechnung von Bahnstörungen

Wegen der Vielzahl der oben aufgeführten Vereinfachungen – Einführung des Begriffes „Flugbahn“ usw. – ist klar, dass alle Versuche, das Sonnensystem in Formeln zu fassen, immer nur Teilaspekte modellieren können.

Dieser Abschnitt erläutert die Verfahren und Vereinfachungen, die zur Anwendung gelangen, allgemeinverständlich. Detailliertere Informationen zu den Rechenverfahren finden sich unter Satellitenbahnelement und Bahnstörungen eines Satelliten.

Häufiger Fehler

Weil dieser Fehler den Medien regelmäßig unterläuft, hier ein kurzer Hinweis: Die Auswirkungen anderer Himmelskörper (Planeten) lassen sich nicht einfach durch den Vergleich der relativen Stärke ihrer Gravitations-(Kraft-)felder abschätzen. Die energetischen Auswirkungen der Störungen durch andere Planeten folgen vielmehr aus der Tatsache, dass sich die Erde auf ihrer Bahn um die Sonne im Gravitationspotential des jeweiligen Planeten um ca. 300 Millionen Kilometer auf und ab bewegt.

Analytische Näherungsverfahren

Ein einfaches Näherungsverfahren zur Berechnung der Periheldrehung der Bahn eines Planeten vereinfacht die (von diesem Planeten aus betrachtet) inneren Planeten zu Massenpunkten im Zentrum der Sonne, und die äußeren Planeten zu Masseringen mit der Gesamtmasse des betreffenden äußeren Planeten. Die Analyse liefert die Bahn des untersuchten Planeten wieder als Keplerbahn, deren Perihel sich aber langsam um die Sonne dreht. Dies ist die sogenannte Periheldrehung. (Genauer gesagt, ist dies die Periheldrehung der Newtonschen Gravitationstheorie, die Allgemeine Relativitätstheorie liefert eine etwas abweichende Periheldrehung.)

Die Anwendung solcher und ähnlicher analytischer Verfahren wird als Störungsrechnung bezeichnet.

Numerische Verfahren

Die Finite-Elemente-Methode und Numerische Integration bieten prinzipiell die Möglichkeit, ein Raumvolumen wie das Sonnensystem oder ein Planet-Satelliten-System in kleine Raumeinheiten (z. B. Würfel) mit bestimmten Eigenschaften zu unterteilen und die Wechselwirkung dieser Raumeinheiten untereinander in diskreten zeitlichen Schritten zu berechnen. Diese Methode stößt wegen der dafür benötigten Rechenzeit an Grenzen.

In einem weiteren Vereinfachungsschritt wird den Planeten ein Massenschwerpunkt zugewiesen, bzw. einem Planeten mit Monden ein Systemschwerpunkt. Dann wird in kleinen zeitlichen Schritten jeweils berechnet, wie sich diese Punkte unter dem Einfluss der Gravititation bewegen würden (numerische Integration). Dies ähnelt der Finite-Elemente-Methode auf einem groben Raster.

Ephemeriden

Die Bahnen der Systemschwerpunkte und der darin enthaltenen Massenpunkte der Himmelskörper im Sonnensystem werden periodisch in den Ephemeriden (Planetentafeln) von renommierten Observatorien veröffentlicht. Zusätzlich wird dabei berücksichtigt, dass ein Beobachter sich auf der Oberfläche der Erde befindet und nicht in ihrem Massenschwerpunkt sitzt, und dass die Atmosphäre und die relative Geschwindigkeit der Körper untereinander optische Effekte verursachen.

Die Ephemeriden können in ganz verschiedenen Koordinatensystemen relevant sein (bzw. werden in solchen Tabellen veröffentlicht), zum Beispiel als Koordinaten der Himmelskörper (bzw. der Schwerpunkte von Planet-Mond-Systemen) in einem Bezugssystem, dessen Mittelpunkt ein nichtrotierendes Koordinatensystem im Schwerpunkt des Sonnensystems ist. Nichtrotierend ist relativ zu den fernen Sternen definiert. Streng genommen ist dies nicht identisch mit dem heliozentrischen System, da sich der Schwerpunkt der Sonne nicht genau im Schwerpunkt des Sonnensystems befindet. Aus diesen Koordinaten kann dann errechnet werden, wie sich ein Himmelskörper einem Astronomen an einem bestimmten Ort zu einer bestimmten Zeit zeigen würde.

Siehe auch

• Kozai-Effekt: Bahnstörung eines kleineren Objektes im Zuge des Dreikörperproblems
• Jarkowski-Effekt: Bahnstörung aufgrund schwankender Oberflächenerwärmung
• YORP-Effekt: Änderung der Rotationsbewegung eines Objektes aufgrund von Wärmeeinstrahlung
• Poynting-Robertson-Effekt: Bahnabbremsung von Partikeln aufgrund des Strahlungsdrucks der Sonne
• Apsidendrehung oder auch Periheldrehung: „Rotation“ der Ellipsenbahn um den Zentralkörper

Literatur

• Ernst Messerschmid, Stefanos Fasoulas: Raumfahrtsysteme. Eine Einführung mit Übungen und Lösungen. 3. neu bearbeitete Auflage. Springer, Berlin u. a. 2009, ISBN 978-3-540-77699-4.
• Ulrich Walter: Astronautics. Wiley-VCH-Verlag GmbH & Co. KGaA, Weinheim 2008, ISBN 978-3-527-40685-2 (Physics Textbook).
• Wiley J. Larson, James R. Wertz (Hrsg.): Space Mission Analysis and Design. 3. edition, 8. printing. Microcosm Press u. a., El Segundo CA u. a. 2006, ISBN 0-7923-5901-1 (Space Technology Library).
• Udo Renner, Joachim Nauck, Nikolaos Balteas: Satellitentechnik. Eine Einführung. Springer, Berlin u. a. 1988, ISBN 3-540-18030-3.

Weblinks

• Ahmed, Kamran (2005): "Obrital Perturbation" (pdf), Präsentation
• Bauer, Oliver (2002): "Ozeangezeitenlösung aus Bahnstörungen erdnaher Satelliten" (pdf), Geodätisches Institut der Universität Stuttgart und GeoForschungsZentrum Potsdam, Diplomarbeit
• Daubrawa, Julian (2007): "Bahnstörungen durch Ozeangezeiten" (pdf), Geodätisches Institut Stuttgart, IfEN GmbH, Diplomarbeit
• Eshagh, M; Najafi Alamdari, M. (2007): "Perturbations in orbital elements of a low earth orbiting satellite" (pdf), Journal of the Earth & Space Physics. Vol. 33, No. 1, P. 1-12, Artikel
• Flechtner, Frank (2010): "Beobachtung von Massenverteilung und Massenvariationen im System Erde mit den Satelliten CHAMP, GRACE, GOCE" (pdf), Deutsches GeoForschungsZentrum - GFZ, Präsentation
• Montag, Horst (2005): "Zu relativistischen Effekten in der Satelliten- bzw. Raumgeodäsie" (pdf), Sitzungsbericht der Leibniz-Sozietät 78/79 2005, S. 277-290, Bericht
• Pressezentrum: "Die Erde als Kartoffel - Das Potsdamer Geoid" (pdf), Helmholtz-Zentrum Potsdam, Deutsches GeoForschungsZentrum – GFZ, Telegrafenberg, 14473 Potsdam, Presseinformation
• Meisinger, R.; Karaca, T.; Taufer, M. (2002): "Simulation der Wiedereintrittsbahn der ISS – Rettungskapsel" (pdf), ISSN 1616-0762 Sonderdruck Schriftenreihe der Georg-Simon-Ohm-Fachhochschule Nürnberg Nr. 12

Einzelnachweise

1. ↑ Sneewu, Nico (2006): Lectures Notes, S.30/31, Institute of Geodesy, Universität Stuttgart (englisch)
2. ↑ Gräßlin, Michael (2004): Widereintritts-Satellit – Ein Satellit kommt zurück, Vorlesung, Universität Stuttgart