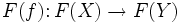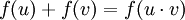- Isomorphe Gruppe
-
In der Mathematik ist ein Isomorphismus eine Abbildung zwischen zwei mathematischen Strukturen, durch die Teile einer Struktur auf „bedeutungsgleiche“ Teile einer anderen Struktur umkehrbar eindeutig (bijektiv) abgebildet werden.
Inhaltsverzeichnis
Definition
Eine Funktion f zwischen zwei Strukturen heißt Isomorphismus, wenn:
- f bijektiv ist,
- f ein Homomorphismus ist,
- die Umkehrfunktion f -1 ein Homomorphismus ist.
Gibt es einen Isomorphismus zwischen zwei Strukturen, dann heißen die beiden Strukturen zueinander isomorph. Isomorphe Strukturen sind in gewisser Weise „dasselbe“, nämlich dann, wenn man von der Darstellung der Elemente der zugrundeliegenden Mengen und den Namen der Relationen und Verknüpfungen absieht.
Die Aussage „X und Y sind isomorph“ wird üblicherweise als
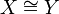 geschrieben; es sind aber auch die Zeichen
geschrieben; es sind aber auch die Zeichen 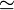 oder
oder 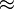 üblich.
üblich.Man beachte, dass bei Gruppen, Ringen, Körpern, Vektorräumen und einigen anderen Strukturen die dritte Bedingung aus den anderen beiden folgt, man im Allgemeinen jedoch nicht auf sie verzichten kann.
Definition in der Kategorientheorie
In der Kategorientheorie wird die oben angegebene Definition noch verallgemeinert. Ein Morphismus
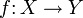 heißt ein Isomorphismus, wenn er ein beidseitiges Inverses
heißt ein Isomorphismus, wenn er ein beidseitiges Inverses 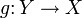 besitzt, d. h.
besitzt, d. h.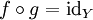 und
und 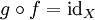 .
.
Spezialfälle dieses Isomorphiebegriffes sind beispielsweise Homöomorphismen als Isomorphismen in der Kategorie der topologischen Räume und stetigen Abbildungen oder Homotopieäquivalenzen als Isomorphismen in der Kategorie der topologischen Räume mit den Homotopieklassen von Abbildungen als Morphismen.
Bedeutung
Oft kann man bestimmte Strukturen nur bis auf Isomorphie eindeutig bestimmen, wie z.B.
- den einzigen endlichen Körper der Ordnung pn,
- den algebraischen Abschluss eines Körpers,
- die Vervollständigung eines metrischen Raums.
Isomorphismen werden in der Mathematik gern ausgenutzt, um einen leichteren Rechenweg zu beschreiten. Durch die oben genannten Definitionen (bijektiv) ist dies möglich.
Beispiele: Laplace-Transformation; s-Transformation
In der Kategorientheorie ist von entscheidender Bedeutung, dass Funktoren Isomorphismen erhalten, d. h. ist
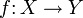 ein Morphismus in einer Kategorie C und
ein Morphismus in einer Kategorie C und 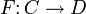 ein Funktor, dann ist
ein Funktor, dann istein Isomorphismus in der Kategorie D. In der algebraischen Topologie wird diese Eigenschaft häufig ausgenutzt, um Räume unterscheiden zu können: Sind beispielsweise die Fundamentalgruppen zweier Räume nicht isomorph, so sind die Räume nicht homöomorph.
Beispiele
Sind
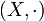 und
und 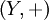 Mengen mit einer binären Verknüpfung, dann ist ein Isomorphismus von X nach Y eine Bijektion
Mengen mit einer binären Verknüpfung, dann ist ein Isomorphismus von X nach Y eine Bijektion 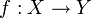 mit
mitfür alle
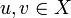 . So ist etwa der Logarithmus ein Isomorphismus von
. So ist etwa der Logarithmus ein Isomorphismus von 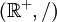 nach
nach 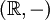 , da
, da 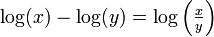 .
.Sind die Strukturen Gruppen, dann heißt ein solcher Isomorphismus Gruppenisomorphismus. Meist meint man mit Isomorphismen solche zwischen algebraischen Strukturen wie Gruppen, Ringen, Körpern oder Vektorräumen.
Sind
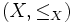 und
und 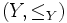 total geordnete Mengen, dann ist ein Isomorphismus von X nach Y eine ordnungserhaltende Bijektion. Diese Isomorphismen spielen in der Theorie der Ordinalzahlen eine wichtige Rolle.
total geordnete Mengen, dann ist ein Isomorphismus von X nach Y eine ordnungserhaltende Bijektion. Diese Isomorphismen spielen in der Theorie der Ordinalzahlen eine wichtige Rolle.Sind
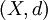 und
und 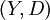 metrische Räume und ist f ein Isomorphismus von X nach Y mit der Eigenschaft
metrische Räume und ist f ein Isomorphismus von X nach Y mit der Eigenschaft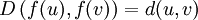 für alle
für alle 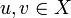 ,
,
dann nennt man man f einen isometrischen Isomorphismus.
In der universellen Algebra kann man eine allgemeine Definition eines Isomorphismus angeben, die diese und andere Situationen abdeckt. Die Definition eines Isomorphismus in der Kategorientheorie ist noch allgemeiner.
Lässt man in den gegebenen Beispielen die Forderung der Bijektivität weg, erhält man jeweils Homomorphismen.
Siehe auch
Weblinks
Wikimedia Foundation.