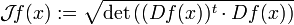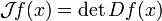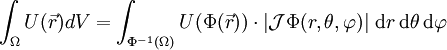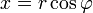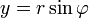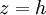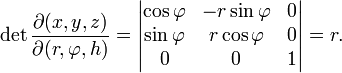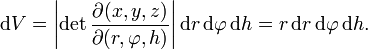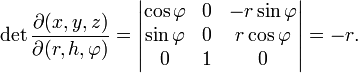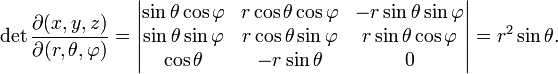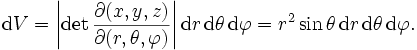Jacobideterminante

Die Funktionaldeterminante oder Jacobi-Determinante ist eine mathematische Größe, die in der mehrdimensionalen Integralrechnung, also der Berechnung von Oberflächen- und Volumenintegralen, eine Rolle spielt. Insbesondere findet sie in der Flächenformel und dem aus dieser hervorgehenden Transformationssatz Verwendung.

Lokales Verhalten einer Funktion

Die Funktionaldeterminante gibt zu einem gegebenen Punkt wichtige Informationen über das Verhalten der Funktion f in der Nähe dieses Punktes. Wenn beispielsweise die Funktionaldeterminante einer stetig differenzierbaren Funktion in einem Punkt p nicht null ist, so ist die Funktion in einer Umgebung von p invertierbar. Weiterhin gilt, dass bei positiver Determinante in p die Funktion ihre Orientierung beibehält und bei negativer Funktionaldeterminante die Orientierung umkehrt. Der absolute Wert der Determinante im Punkt p gibt den Wert an, mit dem die Funktion in der Nähe von p expandiert oder schrumpft.

Definition

Die Funktionaldeterminante einer Funktion 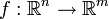$f: \R^n \to \R^m$ ist definiert als

$\mathcal J \! f(x) := \sqrt{\det \left( (Df(x))^t \cdot Df(x) \right)}$

Dabei bezeichnet Df(x) die Jacobi-Matrix und (Df(x))^t ihre Adjungierte.

Im Fall einer Selbstabbildung 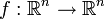$f: \R^n \to \R^n$ gilt

$\mathcal J \! f(x) = \det Df(x)$

in Übereinstimmung mit der intuitiven Interpretation des Begriffes.

Beispiele

Bei der Integration über geometrische Objekte ist es oft unpraktisch, über kartesische Koordinaten zu integrieren. So lässt sich in der Physik das Integral über ein radialsymmetrisches Potentialfeld, dessen Wert nur von einem Radius r abhängt, wesentlich leichter in Kugelkoordinaten berechnen.

Um dies zu tun, wendet man eine Koordinatentransformation Φ an. Nach dem Transformationssatz gilt dann in diesem Beispiel:

$\int_{\Omega} U(\vec r) dV = \int_{\Phi^{-1}(\Omega)} U(\Phi(\vec r)) \cdot \left|\mathcal J \Phi(r, \theta, \varphi)\right| \,\mathrm{d}r \,\mathrm{d}\theta \,\mathrm{d}\varphi$

Im Folgenden sind Rechnungen zu zwei Koordinatensystemen aufgeführt:

Zylinderkoordinaten

Die Umrechnungsformeln von Zylinderkoordinaten (r, $\varphi$, h) in kartesische Koordinaten lauten:

$x = r \cos\varphi$

$y = r \sin\varphi$

$\! z = h$

Die Funktionaldeterminante lautet also:

$\det\frac{\partial(x,y,z)}{\partial(r,\varphi,h)}=\begin{vmatrix} \cos\varphi & -r\sin\varphi & 0 \\ \sin\varphi & r\cos\varphi & 0 \\ 0 & 0 & 1 \end{vmatrix}=r.$

Folglich ergibt sich für das Volumenelement dV:

$\mathrm{d}V=\left|\det \frac{\partial(x,y,z)}{\partial(r,\varphi,h)} \right| \mathrm{d}r \,\mathrm{d}\varphi \,\mathrm{d}h=r \,\mathrm{d}r\, \mathrm{d}\varphi \, \mathrm{d}h.$

Genauso gut hätte man eine andere Reihenfolge der Zylinderkoordinaten wählen können. Die Funktionaldeterminante lautet dann beispielsweise:

$\det\frac{\partial(x,y,z)}{\partial(r,h,\varphi)}=\begin{vmatrix} \cos\varphi & 0 & -r\sin\varphi \\ \sin\varphi & 0 & r\cos\varphi \\ 0 & 1 & 0 \end{vmatrix}=-r.$

In das Transformationsgesetz geht jedoch immer nur der Betrag der Determinante ein, also ist das Ergebnis dann unabhängig von der gewählten Reihenfolge der Variablen, nach denen abgeleitet wird.

Kugelkoordinaten

Die Umrechnungsformeln von Kugelkoordinaten (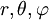$r, \theta,\varphi$) in kartesische Koordinaten lauten:

$x = r \sin \theta \cos \varphi$,

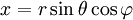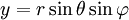$y = r \sin \theta \sin \varphi$ und

$z = r \cos \theta \quad$.

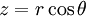Die Funktionaldeterminante lautet also:

$\det\frac{\partial(x,y,z)}{\partial(r, \theta, \varphi)}=\begin{vmatrix} \sin\theta\cos\varphi&r\cos\theta\cos\varphi&-r\sin\theta\sin\varphi\\ \sin\theta \sin\varphi&r\cos\theta\sin\varphi&r\sin\theta\cos\varphi\\ \cos\theta&-r\sin\theta&0 \end{vmatrix}=r^2\sin\theta.$

Folglich ergibt sich für das Volumenelement dV:

$\mathrm{d}V=\left|\det \frac{\partial(x,y,z)}{\partial(r,\theta,\varphi)} \right| \mathrm{d}r \,\mathrm{d}\theta \,\mathrm{d}\varphi=r^2 \sin\theta \,\mathrm{d}r\, \mathrm{d}\theta\, \mathrm{d}\varphi.$