Koordinatensingularität

Dieser Artikel wurde den Mitarbeitern der Redaktion Physik zur Qualitätssicherung aufgetragen. Wenn Du Dich mit dem Thema auskennst, bist Du herzlich eingeladen, Dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Koordinatensingularitäten an Nord- und Südpol einer Sphäre bei Verwendung geographischer Koordinaten

In der Physik spricht man von einer Koordinatensingularität, wenn ein Koordinatensystem aufgrund seiner besonderen Eigenschaften für einen bestimmten Punkt keine eindeutigen Koordinaten angeben kann. So sind zum Beispiel an Nord- und Südpol der Erde eindeutige Angaben zur geografischen Länge weder möglich noch erforderlich, da sich alle Längenkreise in diesem Punkt schneiden. Anders als eine physikalische Singularität ist eine Koordinatensingularität für einen Beobachter ohne Auffälligkeit, da sie nur aufgrund der Eigenschaften des Koordinatensystems erscheint. Sie verschwindet bei Anwendung eines geeigneteren Koordinatensystems.

Definition

Ein Punkt ${\mathbf g}$ einer n-dimensionalen Untermannigfaltigkeit G des euklidischen Raums $\R^m$ mit $m \geq n$ oder einer (abstrakten) Mannigfaltigkeit dieser Dimension, lässt sich durch Wahl eines Koordinatensystems mit Hilfe von Koordinaten $(v_1, v_2, \ldots , v_n)$ mit $v_1, \ldots , v_n \in \R$ identifizieren. Der Einfachheit halber soll es sich dabei um orthogonale Koordinaten handeln, das heißt der Punkt ${\mathbf g} \in G$ habe die Darstellung

${\mathbf g} = v_1 \cdot {\mathbf e}_1 + v_2 \cdot {\mathbf e}_2 + \ldots + v_n \cdot {\mathbf e}_n,$

wobei die n Einheitsvektoren ${\mathbf e}_1, \ldots , {\mathbf e}_n$ eine Orthonormalbasis bilden. Eine Koordinatensingularität entsteht an einem Punkt ${\mathbf g} \in G$, wenn dieser Punkt in dem gewählten Koordinatensystem keine eindeutigen Koordinaten besitzt, also auch durch einen anderen Koordinatenvektor $(v'_1, \ldots , v'_n)$ repräsentiert wird.

Eigenschaften

Die Natur einer solchen Koordinatensingularität erkennt man, wenn man ein anderes Koordinatensystem betrachtet, in dem jeder Punkt ${\mathbf g} \in G$ eindeutige orthogonale Koordinaten $(x_1, \ldots , x_n)$ besitzt. Im Fall des Euklidischen Raums können dies kartesische Koordinaten sein, im Fall von Mannigfaltigkeiten kann dies mit einer Menge von Karten geschehen. Dann gibt es eine Koordinatentransformation T der Form

$(x_1, \ldots , x_n) = T(v_1, \ldots , v_n),$

die allerdings an einer Koordinatensingularität nicht invertierbar ist, da $T(v_1, \ldots , v_n) = T(v'_1, \ldots , v'_n)$ gilt. Ist die Koordinatentransformation T komponentenweise differenzierbar, was bei gängigen Koordinatensystemen der Fall ist, dann ist die Jacobi-Matrix

$J(T) = \frac{\partial(x_1, \ldots , x_n)}{\partial(v_1, \ldots , v_n)}$

an einer Koordinatensingularität singulär, daher die Bezeichnung „Koordinatensingularität“.

Beispiele

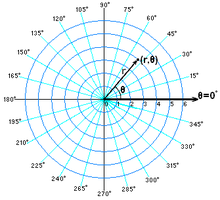
Polarkoordinaten

Polarkoordinaten $\scriptstyle(r, \theta)$

Im Polarkoordinatensystem wird jeder Punkt der Ebene durch eine Radialkoordinate $r \in \R_{+}$ und eine Winkelkoordinate $\theta \in (-\pi,\pi]$ beschrieben. Die Umrechnung von Polarkoordinaten in kartesische Koordinaten $(x,y) \in \R^2$ erfolgt durch die Koordinatentransformation

$x = r \cdot \cos \theta$

$y = r \cdot \sin \theta$

Im Nullpunkt (0,0) erhält man dabei eine Koordinatensingularität: ist r = 0, so ist das Ergebnis der Transformation unabhängig von der Winkelkoordinate θ. In Polarkoordinaten hat der Nullpunkt damit keine eindeutige Darstellung. Erweitert man Polarkoordinaten um eine Höhenkoordinate h, die den Abstand von der Ebene des Polarkoordinatensystems angibt,

z = h

erhält man Zylinderkoordinaten des Raumes, die an allen Punkten (0,0,z) singulär sind.

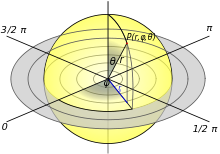
Kugelkoordinaten

Kugelkoordinaten $\scriptstyle(r, \phi, \theta)$

Im Kugelkoordinatensystem wird jeder Punkt des Raums durch eine Radialkoordinate $r \in \R_{+}$ und zwei Winkelkoordinaten $\phi \in (-\pi,\pi]$ und $\theta \in [0,\pi]$ beschrieben. Die Umrechnung von Kugelkoordinaten in kartesische Koordinaten $(x,y,z) \in \R^3$ erfolgt durch die Koordinatentransformation

$x = r \cdot \sin \theta \cdot \cos \varphi$

$y = r \cdot \sin \theta \cdot \sin \varphi$

$z = r \cdot \cos \theta$

Man erhält durch diese Transformation die folgenden Koordinatensingularitäten:

• ist θ = 0, so ist das Ergebnis der Transformation der Punkt (0,0,r) auf der positiven z-Achse unabhängig von der Winkelkoordinate φ
• ist θ = π, so ist das Ergebnis der Transformation der Punkt (0,0, − r) auf der negativen z-Achse unabhängig von der Winkelkoordinate φ
• ist r = 0, so ist das Ergebnis der Transformation der Nullpunkt (0,0,0) unabhängig von beiden Winkelkoordinaten φ und θ

In Kugelkoordinaten hat somit die gesamte z-Achse keine eindeutige Darstellung. Durch Setzen von r = 1 erhält man sphärische Koordinaten (geographische Koordinaten) auf der Kugeloberfläche, die nur an den beiden Polen (0,0,1) und (0,0, − 1) singulär sind.

Siehe auch

• Schwarzschild-Metrik

Literatur

• Franz Embacher: Mathematische Grundlagen für das Lehramtsstudium Physik. 2. Auflage. Vieweg+Teubner, Wiesbaden 2008, ISBN 978-3-8348-0948-3, S. 167 (Online).
• Hans Jörg Dirschmid: Tensoren und Felder. 1. Auflage. Springer, Wien 1996, ISBN 978-3211827543, S. 492 (Online).
• Thomas Filk,Domenico Giulini: Am Anfang war die Ewigkeit: auf der Suche nach dem Ursprung der Zeit. 1. Auflage. Beck, München 2004, ISBN 978-3406521874, S. 243 (Online).