- Köthe-Raum
-
Ein Folgenraum ist ein in der Mathematik betrachteter Raum, dessen Punkte Zahlenfolgen sind. Viele in der Funktionalanalysis auftretende Vektorräume sind Folgenräume oder können durch solche repräsentiert werden. Zu den Beispielen zählen u.a. die wichtigen Räume wie
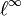 aller beschränkten Folgen oder c0 aller gegen 0 konvergenten Folgen. Die Folgenräume bieten vielfältige Möglichkeiten zur Konstruktion von Beispielen und können daher auch als eine Spielwiese für Funktionalanalytiker betrachtet werden.
aller beschränkten Folgen oder c0 aller gegen 0 konvergenten Folgen. Die Folgenräume bieten vielfältige Möglichkeiten zur Konstruktion von Beispielen und können daher auch als eine Spielwiese für Funktionalanalytiker betrachtet werden.Inhaltsverzeichnis
Einführung
Mit ω wird der Vektorraum aller Folgen in
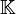 (=
(= 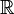 oder
oder  ) bezeichnet. Folgen können komponentenweise addiert und mit reellen bzw. komplexen Zahlen multipliziert werden. Sind etwa
) bezeichnet. Folgen können komponentenweise addiert und mit reellen bzw. komplexen Zahlen multipliziert werden. Sind etwa 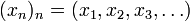 und
und 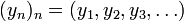 solche Folgen und ist
solche Folgen und ist 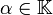 , so ist
, so ist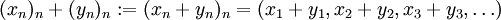
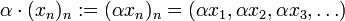 .
.Es ist klar, dass ω mit diesen Operationen ein
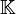 -Vektorraum ist. Folgenräume sind Unterräume dieses Vektorraums, die, um eine Mindestreichhaltigkeit zu sichern, alle Folgen e(n), die an der n-ten Stelle 1 und sonst überall 0 sind, enthalten.
-Vektorraum ist. Folgenräume sind Unterräume dieses Vektorraums, die, um eine Mindestreichhaltigkeit zu sichern, alle Folgen e(n), die an der n-ten Stelle 1 und sonst überall 0 sind, enthalten.Der kleinste Folgenraum ist damit der von den Folgen e(n) erzeugte Unterraum. Dieser wird mit c00 bezeichnet und besteht aus allen Folgen, die nur an endlichen vielen Stellen von 0 verschieden sind. Man nennt ihn daher auch den Raum der endlichen Folgen, wobei man sich jede endliche Folge durch Nullen zu einer unendlichen Folge fortgesetzt denkt. Also sind Folgenräume Unterräume von ω, die c00 enthalten.
Der Umstand, dass die Elemente eines Folgenraums Folgen sind, die man als Elemente eines Vektorraums auch einfach Punkte oder Vektoren nennt, kann zu Missverständnissen führen. Insbesondere wenn man Folgen in solchen Räumen betrachtet, hat man es mit Folgen von Folgen zu tun.
Wir werden gleich Normen bzw. Systeme von Normen oder Halbnormen auf Folgenräumen definieren und dadurch normierte Räume bzw. lokalkonvexe Räume erhalten.
c0 und c
Die wohl bekanntesten Folgenräume sind der Raum c0 aller gegen 0 konvergenten Folgen und der Raum c aller konvergenten Folgen. Betrachtet man auf diesen Räumen die Supremumsnorm, d.h.
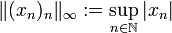 , so erhält man Banachräume. c0 ist ein 1-kodimensionaler Unterraum von c. Bezeichnet nämlich e die konstante Folge, die an jeder Stelle gleich 1 ist, so gilt offenbar
, so erhält man Banachräume. c0 ist ein 1-kodimensionaler Unterraum von c. Bezeichnet nämlich e die konstante Folge, die an jeder Stelle gleich 1 ist, so gilt offenbar 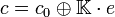 . Mit der komponentenweise erklärten Multiplikation sind c0 und c Banachalgebren, sogar C*-Algebren. Weiter kann man zeigen, dass
. Mit der komponentenweise erklärten Multiplikation sind c0 und c Banachalgebren, sogar C*-Algebren. Weiter kann man zeigen, dass 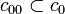 dicht liegt. Beide Räume sind damit separabel, denn die Menge aller endlichen Folgen mit Werten aus
dicht liegt. Beide Räume sind damit separabel, denn die Menge aller endlichen Folgen mit Werten aus 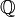 bzw.
bzw. 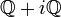 ist abzählbar und dicht.
ist abzählbar und dicht.lp
Es sei
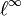 der Raum der beschränkten Folgen mit der Supremumsnorm. Für
der Raum der beschränkten Folgen mit der Supremumsnorm. Für 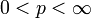 sei
sei .
.Ist 0 < p < 1, so erhält man durch die Definition
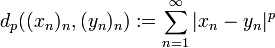 eine Metrik, die
eine Metrik, die  zu einem vollständigen topologischen Vektorraum macht, der kein normierter Raum ist. Für
zu einem vollständigen topologischen Vektorraum macht, der kein normierter Raum ist. Für 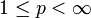 wird durch
wird durch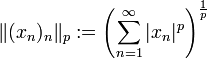
eine Norm definiert (dazu benötigt man die Minkowski-Ungleichung), die
 zu einem Banachraum macht. Der Unterraum c00 liegt dicht und es folgt die Separabilität von
zu einem Banachraum macht. Der Unterraum c00 liegt dicht und es folgt die Separabilität von  für
für 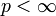 . Der Raum
. Der Raum 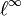 ist nicht separabel. Ist nämlich
ist nicht separabel. Ist nämlich 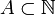 , so sei χA die Folge, die an jeder Komponente aus A gleich 1 und sonst 0 ist. Dann haben die überabzählbar vielen Folgen χA paarweise den
, so sei χA die Folge, die an jeder Komponente aus A gleich 1 und sonst 0 ist. Dann haben die überabzählbar vielen Folgen χA paarweise den 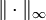 -Abstand 1 voneinander, weshalb
-Abstand 1 voneinander, weshalb 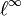 nicht separabel sein kann.
nicht separabel sein kann.Die
 -Räume sind ein Spezialfall der allgemeineren Lp-Räume, wenn man das Zählmaß auf dem Raum
-Räume sind ein Spezialfall der allgemeineren Lp-Räume, wenn man das Zählmaß auf dem Raum  betrachtet.
betrachtet.Unter den
 -Räumen befindet sich der Hilbertraum
-Räumen befindet sich der Hilbertraum  ; nach dem Satz von Fischer-Riesz ist das bis auf isometrische Isomorphie der einzige unendlich-dimensionale separable Hilbertraum. Alle
; nach dem Satz von Fischer-Riesz ist das bis auf isometrische Isomorphie der einzige unendlich-dimensionale separable Hilbertraum. Alle  -Räume sind mit der komponentenweisen Multiplikation Banachalgebren,
-Räume sind mit der komponentenweisen Multiplikation Banachalgebren,  ist eine H*-Algebra,
ist eine H*-Algebra, 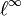 eine C*-Algebra, sogar eine von-Neumann-Algebra.
eine C*-Algebra, sogar eine von-Neumann-Algebra.Dualität
Man sagt, der normierte Folgenraum E hat den normierten Folgenraum F als Dualraum, wenn folgendes gilt:
- Für alle
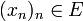 und
und 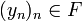 ist
ist 
- Jedes y = (yn)n definiert durch
 ein stetiges lineares Funktional auf E.
ein stetiges lineares Funktional auf E. - Die Abbildung
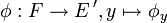 ist surjektiv und isometrisch.
ist surjektiv und isometrisch.
In diesem Sinne liegen folgende Dualitäten vor:
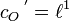 ,
, 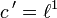
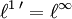
- Ist
 und
und  , so ist
, so ist 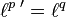 .
.
Lokalkonvexe Räume
Rein algebraisch hat man die Isomorphien
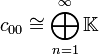 und
und 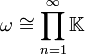 . Damit kann man auf c00 die Summentopologie, d.h. die Finaltopologie aller Inklusionen
. Damit kann man auf c00 die Summentopologie, d.h. die Finaltopologie aller Inklusionen 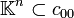 , definieren, was diesen Raum zu einem LF-Raum macht. ω wird durch die Produkttopologie, d.h. durch die Topologie der komponentenweisen Konvergenz, zu einem lokalkonvexen Raum.
, definieren, was diesen Raum zu einem LF-Raum macht. ω wird durch die Produkttopologie, d.h. durch die Topologie der komponentenweisen Konvergenz, zu einem lokalkonvexen Raum.Die oben definierte Dualität für normierte Folgenräume lässt sich auf lokalkonvexe Räume verallgemeinern, wenn man Punkt 3 durch die folgende Forderung ersetzt:
- Die Abbildung
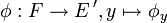 ist ein Homöomorphismus.
ist ein Homöomorphismus.
Dann gilt c00' = ω und
 .
.Köthe-Räume
Die folgende auf Gottfried Köthe zurückgehende Konstruktion von lokalkonvexen Folgenräumen bietet ein reichhaltiges Arsenal an Beispielen.
Unter einer Köthe-Matrix versteht man eine unendliche Matrix A = (an,m)n,m mit folgenden Eigenschaften:
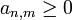 für alle Matrixelemente und zu jedem n gibt es ein m mit an,m > 0.
für alle Matrixelemente und zu jedem n gibt es ein m mit an,m > 0.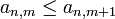 für alle Indizes n,m.
für alle Indizes n,m.
Mit diesen Daten werden nun die folgenden Räume definiert, wobei
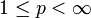 sei:
sei:
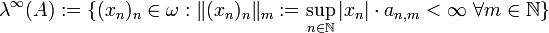
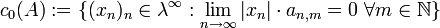 .
.Diese Räume heißen die durch die Köthe-Matrix definierten Köthe-Räume (oder auch Köthe'sche Stufenräume), die Normen
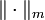 heißen die zugehörigen kanonischen Normen. Jeder dieser Räume wird mit dem System der kanonischen Normen ein lokalkonvexer Raum, sogar ein Fréchet-Raum.
heißen die zugehörigen kanonischen Normen. Jeder dieser Räume wird mit dem System der kanonischen Normen ein lokalkonvexer Raum, sogar ein Fréchet-Raum.Wählt man als Köthe-Matrix die Matrix I, die an jeder Komponente gleich 1 ist, so erhält man die oben definierten normierten Räume zurück:
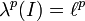 , c0(I) = c0. Indem man Köthe-Matrizen wählt, deren Matrix-Elemente ein bestimmtes Wachstumsverhalten zeigen, kann man Beispiele für ganz andere Raumklassen konstruieren.
, c0(I) = c0. Indem man Köthe-Matrizen wählt, deren Matrix-Elemente ein bestimmtes Wachstumsverhalten zeigen, kann man Beispiele für ganz andere Raumklassen konstruieren.So gilt z.B.:
Für eine Köthe-Matrix A = (an,m)n,m sind folgende Aussagen äquivalent:
- Für jedes
![p\in [1,\infty]](/pictures/dewiki/99/c4c80a6c10fc00791efca5fe92c6ee51.png) ist λp(A) ein Montel-Raum.
ist λp(A) ein Montel-Raum. - c0(A) ist eine Montel-Raum.
- Zu jeder unendlichen Teilmenge
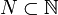 und jedem
und jedem 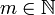 gibt es gibt es ein
gibt es gibt es ein 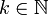 , so dass
, so dass 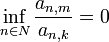 .
.
Für eine Köthe-Matrix A = (an,m)n,m sind folgende Aussagen äquivalent:
- Für jedes
![p\in [1,\infty]](/pictures/dewiki/99/c4c80a6c10fc00791efca5fe92c6ee51.png) ist λp(A) ein Schwartz-Raum.
ist λp(A) ein Schwartz-Raum. - Zu jedem
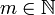 gibt es ein
gibt es ein 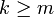 , so dass
, so dass 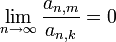 .
.
Für eine Köthe-Matrix A = (an,m)n,m sind folgende Aussagen äquivalent:
- Für jedes
![p\in [1,\infty]](/pictures/dewiki/99/c4c80a6c10fc00791efca5fe92c6ee51.png) ist λp(A) ein nuklearer Raum.
ist λp(A) ein nuklearer Raum. - c0(A) ist eine nuklearer Raum.
- Zu jedem
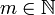 gibt es ein
gibt es ein 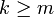 , so dass
, so dass 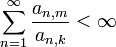 .
.
Als Anwendung dieser Aussagen kann man durch Wahl einer geeigneten Köthe-Matrix Beispiele für Montel-Räume konstruieren, die keine Schwartz-Räume sind. Derartige Beispiele sind sehr wichtig, um etwas Ordnung in den Zoo der lokalkonvexen Räume zu bringen.
Für die Matrix A = (nm)n,m nennt man s: = λ1(A) den Raum der schnell fallenden Folgen. Dieser Raum s spielt eine wichtige Rolle in der Theorie der nuklearen Räume, denn nach dem Satz von Kōmura-Kōmura ist dieser Raum ein Generator aller nuklearen Räume.
Literatur
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume. Lecture Notes in Mathematics 56, 1968.
- H. Jarchow: Locally Convex Spaces. Teubner, Stuttgart 1981, ISBN 3-519-02224-9.
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis. Vieweg, 1992, ISBN 3-528-07262-8.
- Für alle
Wikimedia Foundation.
