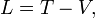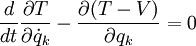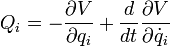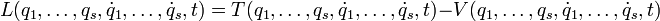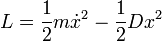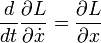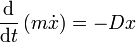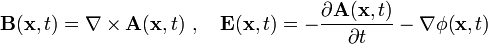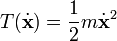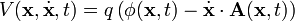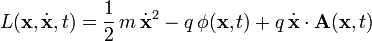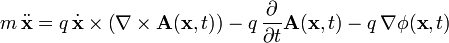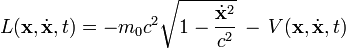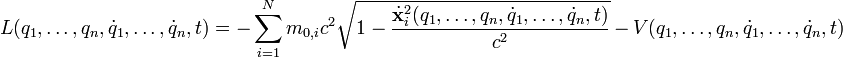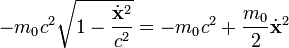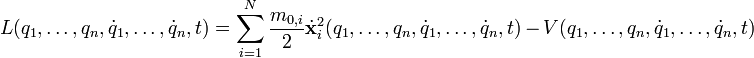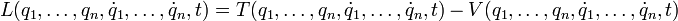- Lagrangian
-
Die Lagrange-Funktion (nach Joseph-Louis Lagrange) ist ein zentrales Element zur Beschreibung von physikalischen Systemen im Lagrange-Formalismus der Klassischen Mechanik. Für konservative Systeme sowie für nicht-konservative Systeme mit einem generalisierten Potential und holonome Zwangsbedingungen lautet sie
wobei T die kinetische und V die potenzielle Energie des betrachteten Systems bezeichnen.
Inhaltsverzeichnis
Mathematischer Ursprung
d'Alembertsches Prinzip in generalisierten Koordinaten
Das d'Alembertsche Prinzip kann geschrieben werden als
![\sum^s_{k=1}\left[\frac{d}{dt}\frac{\partial T}{\partial \dot q_k}-\frac{\partial T}{\partial q_k}-Q_k\right]\delta q_k=0](/pictures/dewiki/49/11c8ed2b55af5d73214d2ed6cb79ea3b.png) ,
,
wobei qk die generalisierten Koordinaten, Qk die generalisierte Kraft, δqk die virtuelle Verrückung der k-ten generalisierten Koordinate und s die Anzahl der Freiheitsgrade bezeichnet.
Betrachtet man das d'Alembert'sche Prinzip für holonome Zwangsbedingungen, so kann man verwenden, dass die generalisierten Koordinaten qk unabhängig sind, wodurch die obige Summe in s einzelne Gleichungen zerlegt werden kann.
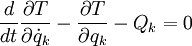 , mit k = 1,...,s
, mit k = 1,...,s
Konservative Kräfte
In einem konservativen System gilt
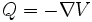 , also für die Komponenten:
, also für die Komponenten: 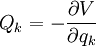
wodurch die Gleichungen umgeschrieben werden können zu
Da die potenzielle Energie V nicht von den generalisierten Geschwindigkeiten
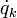 abhängt, kann man auch schreiben
abhängt, kann man auch schreiben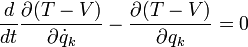 ,
,
weil es bei der Ableitung wieder wegfällt. Dies sind nun jedoch gerade die Lagrange-Gleichungen für eine Funktion :
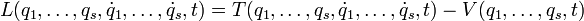 .
.
Spezielle nicht-konservative Kräfte
Lassen sich die generalisierten Kräfte durch ein geschwindigkeitsabhängiges generalisiertes Potential
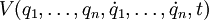 in folgender Form schreiben
in folgender Form schreibenbleiben die Euler-Lagrange-Gleichungen in ihrer gewohnten Form gültig
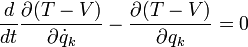 ,
,
und die Lagrangefunktion ist nun:
Beispiele
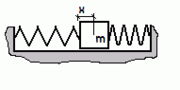
Konservatives System: Masse im harmonischen Potential
Eine Masse m sei über zwei Federn mit Gesamt-Federkonstante D und festen Randbedingungen verbunden (siehe Bild).
Grundvoraussetzung zur Beschreibung des Problems im Lagrange-Formalismus ist das Aufstellen der Lagrange-Funktion, indem man die Terme für kinetische und potentielle Energie aufstellt.
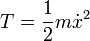 und
und 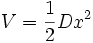
Die Lagrange-Funktion lautet daher:
Die Lagrange-Funktion wiederum wird zur analytischen Beschreibung des physikalischen Problems in die Euler-Lagrange-Gleichung eingesetzt, was dann auf Gleichungen führt, die den Bewegungsgleichungen in der Newtonschen Mechanik entsprechen. In unserem Beispiel lautet die generalisierte Koordinate einfach x, die Euler-Lagrange-Gleichung
und daraus dann
führt auf die Bewegungsgleichung des Systems:
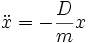 .
.
Die allgemeine Lösung dieser Differentialgleichung ist
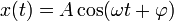 , t ist die Zeit,
, t ist die Zeit, 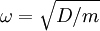 die Kreisfrequenz. Die Amplitude A = const und Phase
die Kreisfrequenz. Die Amplitude A = const und Phase 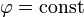 wird aus den Anfangsbedingungen bestimmt.
wird aus den Anfangsbedingungen bestimmt.Nicht-konservatives System: Geladenes Teilchen im elektromagnetischen Feld
Eine Punktladung q Masse m bewege sich im elektromagnetischen Feld. Die generalisierten Koordinaten entsprechen den kartesischen Koordinaten in 3 Raumdimensionen.
Die Felder (Magnetfeld
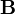 und elektrisches Feld
und elektrisches Feld 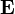 ) werden über das Skalarpotential φ und das Vektorpotential
) werden über das Skalarpotential φ und das Vektorpotential 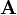 bestimmt:
bestimmt:Die kinetische Energie des Teilchens ist klassisch:
Das Potential ist hier allerdings geschwindigkeitsabhängig:
Somit ist die Lagrangefunktion eines geladenen Teilchens im elektromagnetischen Feld:
Die Euler-Lagrange-Gleichungen
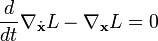 führt auf die Bewegungsgleichung, auf deren rechter Seite die Lorentzkraft steht:
führt auf die Bewegungsgleichung, auf deren rechter Seite die Lorentzkraft steht:Relativistische Mechanik
In der relativistischen Mechanik gilt L = T − V nicht mehr. Dort ist die Lagrangefunktion für ein Teilchen mit Ruhemasse m0 und Geschwindigkeit
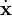 ohne Zwangsbedingungen gegeben durch:
ohne Zwangsbedingungen gegeben durch:Die relativistische kinetische Energie
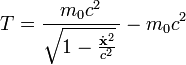 ist nicht mit dem ersten Term identisch.
ist nicht mit dem ersten Term identisch.Für ein N-Teilchensystem ist die Lagrangefunktion mit den generalisierten Koordinaten
wobei n = 3N − s die Anzahl der Freiheitsgrade und s die Anzahl der holonomen Zwangsbedingungen ist.
Für kleine Geschwindigkeiten
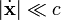 kann man die Wurzel bis zur ersten Ordnung entwickeln
kann man die Wurzel bis zur ersten Ordnung entwickeln 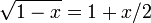 :
:Die nullte Ordnung der Entwicklung ist eine Konstante, die negative Ruheenergie. Da die Euler-Lagrange-Gleichungen invariant sind unter Addition einer Konstanten zur Lagrangefunktion, kann man den konstanten ersten Term vernachlässigen und man erhält wieder die klassische kinetische Energie:
Siehe auch
Weblinks
Literatur
- H. Goldstein: Klassische Mechanik. Wiley-VCH. ISBN 978-3527405893
Wikimedia Foundation.