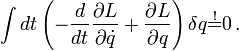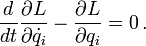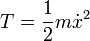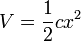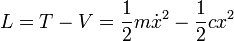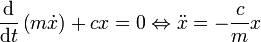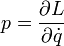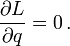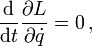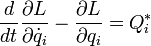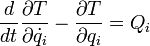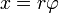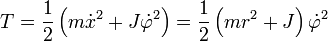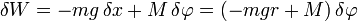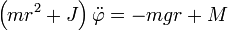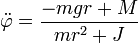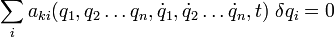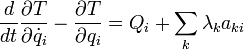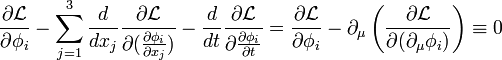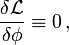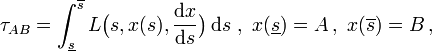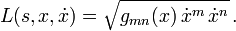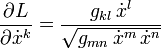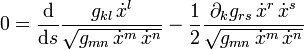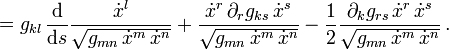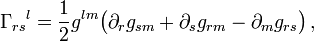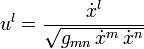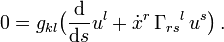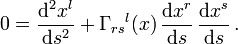- Euler-Lagrange-Gleichungen
-
Der Lagrange-Formalismus ist eine 1788 von Joseph Louis Lagrange eingeführte Formulierung der klassischen Mechanik, in der die Dynamik eines Systems durch eine einzige skalare Funktion, die Lagrangefunktion, beschrieben wird. Dadurch wird automatisch eine Invarianz gegen Koordinatentransformationen in den Formalismus „eingebaut“. Die Bewegungsgleichungen folgen als sogenannte Lagrangegleichungen aus dem Hamiltonschen Prinzip der stationären Wirkung.
Diese Betrachtungsweise vereinfacht viele physikalische Probleme, denn im Gegensatz zur Newton’schen Formulierung der Bewegungsgesetze lassen sich im Lagrange-Formalismus Zwangsbedingungen relativ einfach durch das explizite Ausrechnen der Zwangskräfte oder die Wahl geeigneter Koordinaten qi (generalisierte Koordinaten) berücksichtigen.
Lagrangesche Methode erster Art
Wir betrachten N Punktteilchen im
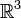 mit den Ortsvektoren
mit den Ortsvektoren 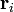 ,
, 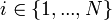 , deren Koordinaten durch s voneinander unabhängige (holonome) Zwangsbedingungen Fk der Form
, deren Koordinaten durch s voneinander unabhängige (holonome) Zwangsbedingungen Fk der Form 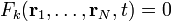 mit
mit 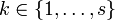 eingeschränkt sind (wobei eine explizite Zeitabhängigkeit zugelassen wurde). Dadurch werden die Lagen der Teilchen auf eine f = 3N − s-dimensionale Mannigfaltigkeit eingeschränkt (f ist die Anzahl der Freiheitsgrade).
eingeschränkt sind (wobei eine explizite Zeitabhängigkeit zugelassen wurde). Dadurch werden die Lagen der Teilchen auf eine f = 3N − s-dimensionale Mannigfaltigkeit eingeschränkt (f ist die Anzahl der Freiheitsgrade).Die Zwangskräfte
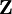 stehen senkrecht auf dieser Mannigfaltigkeit und können daher durch eine Linearkombination der Gradienten
stehen senkrecht auf dieser Mannigfaltigkeit und können daher durch eine Linearkombination der Gradienten 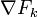 dargestellt werden:
dargestellt werden:Wenn man annimmt, dass sich die äußeren Kräfte aus einem Potential ableiten lassen, kann man die Bewegungsgleichung folgendermaßen schreiben:
Die mi sind die Massen der N Punktteilchen, V ist die potentielle Energie. Dies, zusammen mit den Zwangsbedingungen
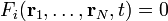 , sind 3N+s unabhängige Gleichungen für die 3N Koordinaten der
, sind 3N+s unabhängige Gleichungen für die 3N Koordinaten der 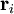 sowie für die s Lagrangemultiplikatoren λk. Somit ist die Lösung des Gleichungssystems eindeutig.
sowie für die s Lagrangemultiplikatoren λk. Somit ist die Lösung des Gleichungssystems eindeutig.Die Lagrangegleichungen erster Art sind äquivalent zu den Gleichungen, die sich aus dem D’Alembertsches Prinzip ergeben.
Bemerkung: Hier wurden nur holonome Zwangsbedingungen behandelt. Der Formalismus lässt sich aber auch auf Zwangsbedingungen der Form
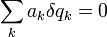 anwenden, die z. B. bei nicht-holonomen Zwangsbedingungen zwischen den Geschwindigkeiten der Teilchen folgen [1]. Diese Zwangsbedingungsgleichungen lassen sich im Gegensatz zu holonomen Zwangsbedingungen nicht als vollständiges Differential einer Funktion darstellen, das heißt zwischen den Koeffizientenfunktionen gilt nicht
anwenden, die z. B. bei nicht-holonomen Zwangsbedingungen zwischen den Geschwindigkeiten der Teilchen folgen [1]. Diese Zwangsbedingungsgleichungen lassen sich im Gegensatz zu holonomen Zwangsbedingungen nicht als vollständiges Differential einer Funktion darstellen, das heißt zwischen den Koeffizientenfunktionen gilt nicht 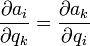 .
.Ähnlich wie oben können die Zwangsbedingungen in den Bewegungsgleichungen über Lagrangemultiplikatoren berücksichtigt werden (siehe unten).
Beispiel – Fallmaschine nach Atwood
Bei der Fallmaschine nach Atwood betracht man zwei Punktmassen im Gravitationsfeld der Erde, die über eine Rolle in der Höhe h aufgehängt und durch ein Seil der Länge l- verbunden seien. Die Zwangsbedingung lautet in diesem Fall:
Wird das Seil berücksichtigt, das auf der Rolle (Rollenradius r) liegt, dann ergibt sich:
Die potentielle Energie V berechnet sich zu:
Für die Gradienten erhält man
Dies führt auf das System der Lagrange-Gleichungen 1. Art:Dies kann man auflösen und erhält z. B. für bekannte Anfangsbedingungen:
Lagrangesche Methode zweiter Art
Herleitung der Lagrange-Gleichungen
Die Lagrange-Funktion der klassischen Mechanik für konservative Systeme mit holonomen Zwangsbedingungen ist
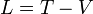 , wobei die kinetische Energie T und die potentielle Energie V mit unterschiedlichem Vorzeichen eingehen.
, wobei die kinetische Energie T und die potentielle Energie V mit unterschiedlichem Vorzeichen eingehen.Die (Euler-)Lagrange-Gleichungen erhält man durch Variation des mit der Lagrangefunktion gebildeten Wirkungsintegrals im Hamiltonschen Prinzip. Dazu variiert man die generalisierten Koordinaten mit
Das Hamiltonsche Prinzip wird dann zu
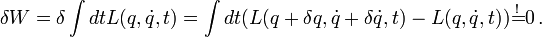 .
.
Eine Näherung in erster Ordnung lautet für eine gewöhnliche Funktion f(x,y)
also
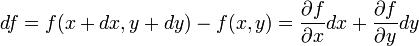 .
.
In erster Ordnung ergibt sich die Variation des Integrals also zu
Nun führt man eine partielle Integration in dem Term aus, der die Ableitung nach der Zeit enthält.
Hierbei wird benutzt, dass
ist, da Anfangs- und Endpunkt festgehalten werden. Daher gilt für die Randterme
Damit resultiert schließlich
Da nun δq als Faktor des gesamten Integrals auftritt und beliebig ist, kann das Integral nur dann nach dem Variationsprinzip verschwinden, wenn der Integrand selbst verschwindet. Es folgen die Euler-Lagrange-Gleichungen (Ursprünglich Euler-Gleichungen aus der Variationsrechnung, hier angewandt auf die Lagrangefunktion), häufig nur kurz als Lagrange-Gleichungen bezeichnet:
Für jede generalisierte Koordinate qi (und die zugehörige generalisierte Geschwindigkeit
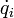 ) gibt es eine solche Gleichung. Die Lagrange-Gleichungen bilden ein System gewöhnlicher Differentialgleichungen zweiter Ordnung.
) gibt es eine solche Gleichung. Die Lagrange-Gleichungen bilden ein System gewöhnlicher Differentialgleichungen zweiter Ordnung.Beispiel
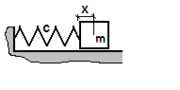
Für einen eindimensionalen harmonischen Oszillator gilt
Mit x als generalisierter Koordinate folgt die Bewegungsgleichung direkt aus der Euler-Lagrange-Gleichung. Die Lagrangefunktion ist
und damit
Die allgemeine Lösung dieser Gleichung ist
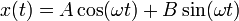 ,
,
wobei
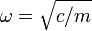 die Kreisfrequenz ist und A,B reelle Konstanten sind.
die Kreisfrequenz ist und A,B reelle Konstanten sind.Zyklische Variable
Wenn die Lagrangefunktion L nicht von einer Koordinate q abhängt, sondern nur von der zugehörigen Geschwindigkeit
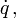 dann nennt man q zyklisch oder zyklische Koordinate oder zyklische Variable. Der zur zyklischen Variablen q konjugierte Impuls
dann nennt man q zyklisch oder zyklische Koordinate oder zyklische Variable. Der zur zyklischen Variablen q konjugierte Impulsist eine Erhaltungsgröße: ihr Wert ändert sich nicht während der Bewegung.
Denn weil die Lagrangefunktion nicht von q abhängt, gilt
Dann besagt die Euler-Lagrangegleichung
dass die Zeitableitung des zugehörigen konjugierten Impulses verschwindet.
Allgemeiner gehört nach dem Noether-Theorem zu jeder kontinuierlichen Symmetrie der Wirkung eine Erhaltungsgröße und umgekehrt zu jeder Erhaltungsgröße eine kontinuierliche Symmetrie der Wirkung. Bei einer zyklischen Variablen ist die Wirkung invariant unter der Verschiebung von q um eine beliebige Konstante,
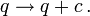
Erweiterung auf nicht-konservative Systeme
Für nicht-konservative Systeme (Systeme, bei denen nicht alle Kräfte Potentialkräfte sind) lassen sich die Lagrangeschen Bewegungsgleichungen wie folgt formulieren:
bzw.
- T: kinetische Energie
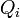 : generalisierte Kräfte als Summe der nicht-konservativen Kräfte und der Potentialkräfte
: generalisierte Kräfte als Summe der nicht-konservativen Kräfte und der Potentialkräfte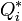 : generalisierte Kräfte ausschließlich nicht-konservativer Natur
: generalisierte Kräfte ausschließlich nicht-konservativer Natur
Die generalisierten Kräfte bestimmt man aus der virtuellen Arbeit der eingeprägten Kräfte
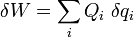
durch Vergleich der Koeffizienten von δqi.
Beispiel
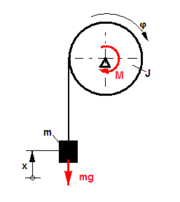
Die Achse einer Aufzugtrommel wird durch ein Moment M angetrieben. Die Masse der Last beträgt m, das Massenträgheitsmoment der Trommel ist J. Der Radius der Trommel ist r.
Zwischen den Koordinaten x und φ besteht folgende Beziehung:
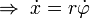
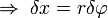
Die kinetische Energie ist:
Die virtuelle Arbeit der eingeprägten Kräfte ist
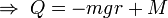
Daraus folgt schließlich die Bewegungsgleichung
Die Auflösung dieser Gleichung nach der Winkelbeschleunigung ergibt
Erweiterung auf Systeme mit Nebenbedingungen
Zwischen den generalisierten Koordinaten mögen noch n Nebenbedingungen folgender Form existieren:
(Nur bei holonomen Systemen lassen sich mit Hilfe der Nebenbedingungen überzählige Koordinaten eliminieren.)
Für Systeme mit Nebenbedingungen lassen sich die Lagrangeschen Bewegungsgleichungen wie folgt formulieren:
- λk: beim Integrationsprozess zu bestimmende Lagrangesche Multiplikatoren
Siehe auch: Hamiltonsche Mechanik
Erweiterung auf Felder
In der Feldtheorie ergibt sich die Bewegungsgleichung aus dem Hamiltonschen Prinzip für Felder zu
wobei Φ = Φ(x,y,z,t) das betrachtete Feld und
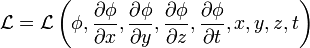 die Lagrange-Dichte sind.
die Lagrange-Dichte sind.Man kann dies in Kurzform auch schreiben als
mit der so definierten Variationsableitung
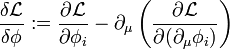 .
.Der Lagrangeformalismus ist auch der Ausgangspunkt vieler Formulierungen der Quantenfeldtheorie.
Zusammenhang mit Pfadintegralen in der Quantenmechanik
Richard Feynman als erster hat diese Herangehensweise auch konsequent für die Herleitung der Gleichungen der Quantenmechanik verwendet. In der klassischen Physik ergeben sich die oben beschriebenen Lagrange-Gleichungen aus der Forderung, dass das Wirkungsintegral (bei dem über die Lagrange-Funktion integriert wird) stationär wird (durch die Variation des Integrals erhält man die Differenzialgleichungen). In Feynmans Pfadintegral-Formalismus ist die quantenmechanische Wahrscheinlichkeitsamplitude, das ein System zwischen Anfangs- und Endbedingungen einen bestimmten Pfad einschlägt proportional
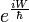 mit dem Wirkungsintegral W. Pfade in der Umgebung des klassischen Weges, für den die Variation von W verschwindet, liefern dabei meist die Hauptbeiträge, da sich in ihrer Umgebung die Beiträge mit fast gleichen Phasenfaktoren addieren. Mehr Details sind im unten angegebenen Lehrbuch online nachzulesen.
mit dem Wirkungsintegral W. Pfade in der Umgebung des klassischen Weges, für den die Variation von W verschwindet, liefern dabei meist die Hauptbeiträge, da sich in ihrer Umgebung die Beiträge mit fast gleichen Phasenfaktoren addieren. Mehr Details sind im unten angegebenen Lehrbuch online nachzulesen.Frei fallende Teilchen in der allgemeinen Relativitätstheorie
In der allgemeinen Relativitätstheorie durchlaufen frei fallende Teilchen Weltlinien längster Zeit: zwischen zwei (genügend nah beieinander liegenden) Ereignissen A und B vergeht auf einer mitgeführten Uhr mehr Zeit, als auf allen anderen Weltlinien durch diese Ereignisse. Sei s ein entlang des Pfades monoton wachsender Laufparameter, so ergibt sich die verstrichene Zeit zu
mit der Lagrangefunktion
Dabei sind gmn(x) die Komponentenfunktionen der Metrik. Wir rechnen einfachheitshalber in Maßsystemen, in denen die Lichtgeschwindigkeit dimensionslos ist und den Wert c = 1 hat, und verwenden die Einsteinsche Summenkonvention.Der zu xk konjugierte Impuls ist
und die Euler-Lagrange-Gleichungen lautenVerwenden wir hier als Abkürzung das Christoffel-Symbol
so erweist sich die Weltlinie längster Dauer als Gerade: die Richtung der Tangente an die Weltlinie
ändert sich nicht bei Parallelverschiebung längs der Weltlinie
Die Parametrisierung wird nicht festgelegt. Verfügen wir so über sie, dass der Tangentialvektor überall gleich lang ist, dann ist
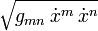 konstant und der Tangentialvektor geht beim Durchlaufen der Weltlinie in sich über. Sie erfüllt die Geodätengleichung
konstant und der Tangentialvektor geht beim Durchlaufen der Weltlinie in sich über. Sie erfüllt die GeodätengleichungDies ist die allgemein-relativistische Form der Bewegungsgleichung eines frei fallenden Teilchens. Die Gravitation ist in den Γrsl voll berücksichtigt.
Literatur
- Lehrbücher der klassischen Mechanik wie
- Herbert Goldstein, Charles P. Poole, John L. Safko: Klassische Mechanik. 3. Auflage. Wiley-VCH, 2006, ISBN 3527405895.
- Cornelius Lanczos: The Variational Principles of Mechanics. 4. Auflage. Dover Pubn Inc, 1986, ISBN 0486650677.
- Friedhelm Kuypers: Klassische Mechanik. 8. Auflage. Wiley-Vch, 2008, ISBN 3527407219.
- zu Pfadintegralen
- Hagen Kleinert: Pfadintegrale in Quantenmechanik, Statistik und Polymerphysik. Spektrum Akad. Vlg., Mannheim 1993, ISBN 3860256130
- Hagen Kleinert: Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets. 4. Auflage, World Scientific, Singapore 2006, ISBN 978-9812700087 ([1] auch online lesbar hier)
Einzelnachweise
- ↑ Die realen anholonomen Zwangsbedingungen wären
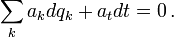 Das Zeitdifferential dt verschwindet per definitionem bei den zugehörigen sog. virtuellen Verschiebungen δqk
Das Zeitdifferential dt verschwindet per definitionem bei den zugehörigen sog. virtuellen Verschiebungen δqk
Weblinks
Wikimedia Foundation.

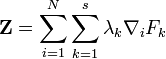
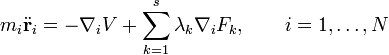
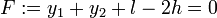
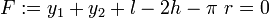
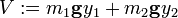
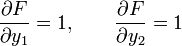
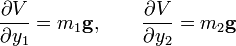
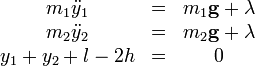
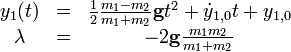
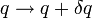
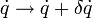
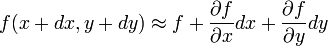
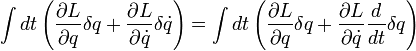
![\int_{t_1}^{t_2} dt \left(\frac{\partial L}{\partial \dot q} \frac{d}{dt} \delta q \right) = \left[\frac{\partial L}{\partial \dot q}\delta q\right]_{t_1}^{t_2} - \int_{t_1}^{t_2} \frac{d}{dt} \frac{\partial L}{\partial \dot q} \delta q \, dt](/pictures/dewiki/48/01ee503440609184ea8cd75661b40c7c.png)
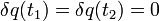
![\left[\frac{\partial L}{\partial \dot q}\delta q\right]_{t_1}^{t_2} = 0](/pictures/dewiki/48/00a7d4ddecf6e110f458d16ec8e74196.png)