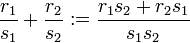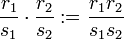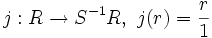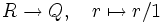- Lokalisation (Ringtheorie)
-
In der Algebra ist Lokalisierung eine Methode, einem Ring R systematisch neue multiplikativ inverse Elemente hinzuzufügen. Möchte man, dass die Elemente einer Teilmenge S von R invertierbar werden, dann konstruiert man einen neuen Ring S − 1R, die „Lokalisierung von R nach S“, und einen Ringhomomorphismus von R nach S − 1R, der S auf Einheiten von S − 1R abbildet. S − 1R und dieser Ringhomomorphismus erfüllen die universelle Eigenschaft der „besten Wahl“.
Inhaltsverzeichnis
Wortherkunft
Die Verwendung des Begriffs „Lokalisierung“ entspringt der algebraischen Geometrie: Ist R ein Ring von reell- oder komplexwertigen Funktionen auf einem geometrischen Objekt (z.B. einer algebraischen Varietät) und will man das Verhalten der Funktionen in der Nähe eines Punktes p untersuchen, dann wählt man für S die Menge der Funktionen, die bei p ungleich 0 sind und lokalisiert R nach S. Die Lokalisierung enthält dann nur noch Informationen über das Verhalten der Funktionen nahe bei p.
Definition
Da die Lokalisierung eines nichtkommutativen Ringes ungleich schwieriger und nicht immer möglich ist, beschränken wir uns in diesem Artikel auf kommutative Ringe mit 1.
Sei also R ein kommutativer Ring mit 1 und S eine Teilmenge von R. Da das Produkt von Einheiten wieder eine Einheit ist, 1 eine Einheit ist, und wir die Elemente von S zu Einheiten machen wollen, können wir S vergrößern und die 1 und alle Produkte von Elementen von S zu S hinzufügen; wir nehmen also gleich an, dass S multiplikativ abgeschlossen ist.
Lokalisierung eines Integritätsbereichs
Im einfachsten Fall ist R ein Integritätsring. Hier unterscheiden wir, ob S die 0 enthält oder nicht.
Ist
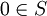 , dann kommt für die Lokalisierung nur der Nullring {0} in Frage, weil er der einzige Ring ist, in dem die 0 Einheit ist. Wir definieren also S − 1R = {0}, falls 0 in S liegt.
, dann kommt für die Lokalisierung nur der Nullring {0} in Frage, weil er der einzige Ring ist, in dem die 0 Einheit ist. Wir definieren also S − 1R = {0}, falls 0 in S liegt.Ist 0 kein Element von S, dann betrachten wir den Quotientenkörper K von R. Der Teilring S − 1R von K, der aus allen Brüchen besteht, deren Zähler in R und deren Nenner in S liegt, hat die gewünschten Eigenschaften: Die kanonische Einbettung von R in K ist ein Ringhomomorphismus, der sogar injektiv ist, und die Elemente von S sind invertierbar. Dieser Ring S − 1R ist der kleinste Teilring von K, der R enthält und in dem die Elemente von S invertierbar sind.
Hier folgen einige Beispiele von Lokalisierungen von Z bezüglich verschiedener Teilmengen S:
- Lokalisiert man Z bzgl. der Menge der ungeraden ganzen Zahlen, erhält man den Ring
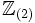 aller rationalen Zahlen mit ungeradem Nenner. Die Verwendung des „(2)“ wird weiter unten erklärt.
aller rationalen Zahlen mit ungeradem Nenner. Die Verwendung des „(2)“ wird weiter unten erklärt. - Lokalisiert man Z bzgl. der Menge der geraden Zahlen ohne die 0, erhält man ganz Q, weil sich jede rationale Zahl durch eventuelle Erweiterung mit 2 als Bruch mit geradem Nenner darstellen lässt.
- Lokalisiert man Z bzgl. der Menge der Zweierpotenzen, erhält man den Ring der Dualbrüche. Dies sind genau die rationalen Zahlen, deren Dualdarstellung nur endlich viele Nachkommastellen hat.
Lokalisierung eines allgemeinen kommutativen Ringes
Für einen beliebigen kommutativen Ring R mit 1 haben wir keinen Quotientenkörper, wir konstruieren also einen neuen Ring, dessen Elemente wir als Brüche aufschreiben werden.
Die folgende Konstruktion liefert für Integritätsringe R einen Ring, der zu dem oben definierten Teilring des Quotientenkörpers isomorph ist.
Auf dem kartesischen Produkt
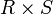 führen wir eine Äquivalenzrelation ein:
führen wir eine Äquivalenzrelation ein:Die Äquivalenzklasse eines Paares (r1,s1) schreiben wir als Bruch
Addition und Multiplikation der Äquivalenzklassen werden analog zu den üblichen Bruchrechenregeln definiert:
Der in der Definition der Äquivalenzrelation auftretende Faktor t ist für die Wohldefiniertheit der Äquivalenzrelation (genauer: der Transitivität) nötig, falls der vorliegende Ring kein Integritätsbereich ist. Mit den so definierten Verknüpfungen erhalten wir einen Ring S − 1R, und die Abbildung
ist ein (nicht notwendig injektiver) Ringhomomorphismus.
Universelle Eigenschaft
Die „beste Wahl“ des Ringes S − 1R und des Homomorphismus
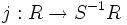 wird durch die Erfüllung einer universellen Eigenschaft definiert:
wird durch die Erfüllung einer universellen Eigenschaft definiert:- Ist R ein kommutativer Ring mit 1, S eine multiplikativ abgeschlossene Teilmenge von R, T ein Ring mit 1,
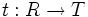 ein Ringhomomorphismus, der jedes Element von S auf eine Einheit abbildet, dann gibt es genau einen Ringhomomorphismus
ein Ringhomomorphismus, der jedes Element von S auf eine Einheit abbildet, dann gibt es genau einen Ringhomomorphismus 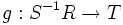 mit
mit 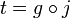 .
.
Die oben definierten Ringe erfüllen diese universelle Eigenschaft.
Häufige Arten der Lokalisierung
Lokalisierung an einem Element
Indem man
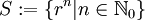 schreibt, lässt man alle Potenzen eines Elementes
schreibt, lässt man alle Potenzen eines Elementes 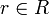 als Nenner zu. Gebräuchliche Schreibweisen dafür sind Rr,
als Nenner zu. Gebräuchliche Schreibweisen dafür sind Rr, ![R\left[\frac1r\right]](/pictures/dewiki/51/3bb95de5e74b6f413e6f0e998ba6276f.png) oder R[r − 1]. Die erhaltene Lokalisierung ist kanonisch isomorph zu R[X] / (rX − 1).
oder R[r − 1]. Die erhaltene Lokalisierung ist kanonisch isomorph zu R[X] / (rX − 1).Lokalisierung nach einem Primideal
Wenn
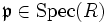 ein Primideal bezeichnet, so spricht man für
ein Primideal bezeichnet, so spricht man für 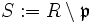 von der „Lokalisierung in
von der „Lokalisierung in 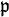 “ oder „nach
“ oder „nach 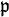 “
“ 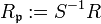 . Der entstehende Ring ist lokal mit dem maximalen Ideal
. Der entstehende Ring ist lokal mit dem maximalen Ideal 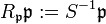 , seine Primideale entsprechen den in
, seine Primideale entsprechen den in 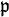 enthaltenen Primidealen. Ist genauer
enthaltenen Primidealen. Ist genauer 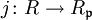 der oben angegebene Ringhomomorphismus, so ist
der oben angegebene Ringhomomorphismus, so ist 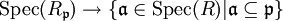 ,
, 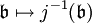 eine inklusionserhaltende Bijektion. Der oben genannte Ring
eine inklusionserhaltende Bijektion. Der oben genannte Ring 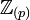 für eine Primzahl p ist ein Beispiel für diese Konstruktion.
für eine Primzahl p ist ein Beispiel für diese Konstruktion.Da
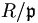 nullteilerfrei ist, kann man den Quotientenkörper bilden. Es gilt dann
nullteilerfrei ist, kann man den Quotientenkörper bilden. Es gilt dann 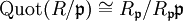 .
.Man kann die Lokalisierung nach einem Primideal auch noch wie folgt deuten: Fasst man Elemente von R als Funktionen auf dem Spektrum von R auf, deren Wert in einem Punkt P das jeweilige Bild im Restklassenkörper
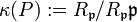 ist, so „besteht“ der lokale Ring bei P aus Brüchen, in deren Nenner Funktionen stehen, die bei P nicht verschwinden, „durch die man also lokal bei P teilen darf“.
ist, so „besteht“ der lokale Ring bei P aus Brüchen, in deren Nenner Funktionen stehen, die bei P nicht verschwinden, „durch die man also lokal bei P teilen darf“.„Ganzabgeschlossen“ ist eine lokale Eigenschaft, d.h. für einen nullteilerfreien Ring R sind äquivalent:
- R ist ganzabgeschlossen
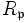 ist ganzabgeschlossen für alle Primideale
ist ganzabgeschlossen für alle Primideale 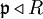
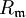 ist ganzabgeschlossen für alle maximalen Ideale
ist ganzabgeschlossen für alle maximalen Ideale 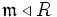
Totalquotientenring
Der Totalquotientenring Q eines Ringes R ist die Lokalisierung von R an der Menge der Nichtnullteiler von R. Er ist die „stärkste“ Lokalisierung, für die die Lokalisierungsabbildung
injektiv ist. Ist R ein Integritätsbereich, so ist der Totalquotientenring der Quotientenkörper von R.
Lokalisierung von Moduln
Ist R ein Ring, S eine multiplikative Teilmenge von R und M ein R-Modul, so ist die Lokalisierung von M bezüglich S definiert als die Menge S−1M der Äquivalenzklassen von Paaren (m,s), auch geschrieben m/s, wobei zwei Paare (m1,s1), (m2,s2) äquivalent sein sollen, wenn es ein Element s von S gibt, so dass
- s(s2m1 − s1m2) = 0
gilt. S−1M ist ein S−1R-Modul.
Entsprechend zum Fall von Ringen schreibt man auch Mr oder MP für Elemente r bzw. Primideale P von R.
Die Lokalisierung eines Moduls besitzt ebenfalls eine universelle Eigenschaft: Jeder R-Homomorphismus von M in einen Modul N, in dem alle Elemente durch die Elemente von S "teilbar" sind, d.h. die Linksmultiplikation mit einem Element aus S ein Modul-Isomorphismus ist, lässt sich auf eindeutige Weise zu einem R-Homomorphismus S−1M → N fortsetzen. Dies bedeutet auch, dass man die Lokalisierung eines Moduls auch als Tensorprodukt beschreiben kann:
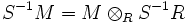 .
.
- Lokalisiert man Z bzgl. der Menge der ungeraden ganzen Zahlen, erhält man den Ring
Wikimedia Foundation.

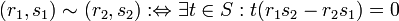
![\frac{r_1}{s_1} := [(r_1, s_1)] := \{(r_2, s_2) \in R \times S : (r_1, s_1) \sim (r_2, s_2)\}](/pictures/dewiki/53/57deda3d992a0193196a668f8ea059e7.png)