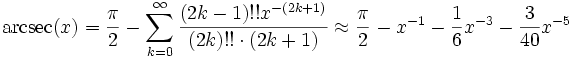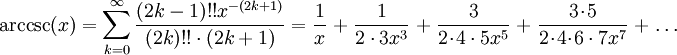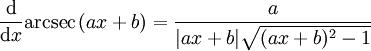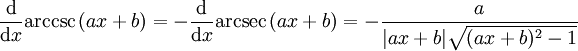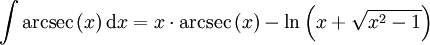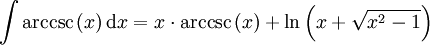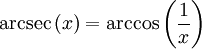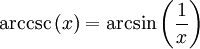- Arkus Kosekans
-
Arkussekans und Arkuskosekans sind trigonometrische Funktionen. Sie sind die Umkehrfunktionen der Sekansfunktion bzw. der Kosekansfunktion und damit Arkusfunktionen. Da die Sekans- und die Kosekansfunktion periodisch sind, wird zur Umkehrung der Definitionsbereich von Sekans auf
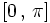 , und der Definitionsbereich von Kosekans auf
, und der Definitionsbereich von Kosekans auf 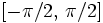 beschränkt. Der Arkussekans wird mit
beschränkt. Der Arkussekans wird mit 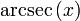 bezeichnet und der Arkuskosekans mit
bezeichnet und der Arkuskosekans mit 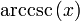 . Seltener, vor allem aber im Englischen verwendet man auch die Schreibweisen sec − 1(x) und csc − 1; sie bedeuten aber nicht, dass
. Seltener, vor allem aber im Englischen verwendet man auch die Schreibweisen sec − 1(x) und csc − 1; sie bedeuten aber nicht, dass 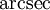 bzw.
bzw. 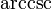 die Kehrwerte von sec und csc sind.
die Kehrwerte von sec und csc sind.Inhaltsverzeichnis
Eigenschaften
Arkussekans Arkuskosekans Funktions-
Graphen

Definitionsbereich 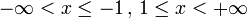
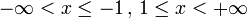
Wertebereich 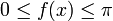
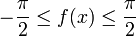
Monotonie In beiden Abschnitten jeweils streng monoton steigend In beiden Abschnitten jeweils streng monoton fallend Symmetrien Punktsymmetrie zum Punkt 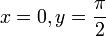
Ungerade Funktion 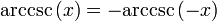
Asymptoten 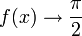 für
für 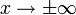
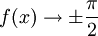 für
für 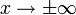
Nullstellen 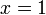
keine Sprungstellen keine keine Polstellen keine keine Extrema Minimum bei 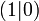 , Maximum bei
, Maximum bei 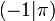
Minimum bei 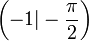 , Maximum bei
, Maximum bei 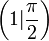
Wendepunkte keine keine Reihenentwicklungen
Die Reihenentwicklungen von Arkussekans und Arkuskosekans sind:
Ableitungen
Die Ableitungen sind gegeben durch:
Integrale
Umrechnung und Beziehungen zu anderen trigonometrischen Funktionen
Siehe auch
Weblinks
- Eric W. Weisstein: Inverse Secant und Inverse Cosecant auf MathWorld
Primäre trigonometrische Funktionen
Sinus und Kosinus | Tangens und Kotangens | Sekans und KosekansUmkehrfunktionen (Arkusfunktionen)
Arkussinus und Arkuskosinus | Arkustangens und Arkuskotangens | Arkussekans und ArkuskosekansHyperbelfunktionen
Sinus Hyperbolicus und Kosinus Hyperbolicus | Tangens Hyperbolicus und Kotangens Hyperbolicus | Sekans Hyperbolicus und Kosekans HyperbolicusAreafunktionen
Areasinus Hyperbolicus und Areakosinus Hyperbolicus | Areatangens Hyperbolicus und Areakotangens Hyperbolicus | Areasekans Hyperbolicus und Areakosekans Hyperbolicus
Wikimedia Foundation.