- Quantisierungsrauschen
-
Als Quantisierungsrauschen bezeichnet man bestimmte Störungen bei der Digitalisierung von Analogsignalen.
Da bei der digitalen Repräsentation nur diskrete Werte möglich sind, müssen die abweichenden analogen Messwerte gerundet werden. Der dabei auftretende Fehler − also die Differenz von Originalsignal zu Digitalsignal − wird als Quantisierungsfehler bezeichnet.
Das analoge Signal wird auf endlich viele Werte abgebildet. Je weniger diskrete Werte zur Verfügung stehen, desto höher ist das resultierende Quantisierungsrauschen; der Signal-Rausch-Abstand sinkt.
Um den Signal-Rausch-Abstand bei einem Informationssignal möglichst hoch zu halten, werden Signale mit kleineren Amplituden bei Bedarf feiner und größere Amplituden gröber aufgelöst, was auch als nichtlineare Quantisierung bezeichnet wird.
Dieses Verfahren findet unter anderem auch in der Telekommunikation Anwendung. Es entstand die genormte 13-Segment-Kennlinie.
Die statistischen und spektralen Eigenschaften des Quantisierungsrauschens hängen vom Originalsignal ab. In der Theorie geht man oft vereinfachend von einem weißen Rauschen aus.
Inhaltsverzeichnis
Messgrößen
Das Quantisierungsrauschen wird durch das Signal-Rausch-Verhältnis (SNR, signal to noise ratio) quantitativ angegeben. Die Signalgüte nimmt mit dem Quadrat der Anzahl der Quantisierungsschritte k zu:
- SNR ≈ k2
Bei N Bits ist k=2N, also:
Um den Signal-Rausch-Abstand des Quantisierungsrauschens genau zu bestimmen, sind die Art der Quantisierung und das zu quantisierende Signal zu berücksichtigen. Für den einfachen Fall einer linearen Puls-Code-Modulation und einem sinusförmigen Signalspannungsverlauf mit Vollpegelaussteuerung am Umsetzer gilt:
bzw in Dezibel
- Herleitung
Zur Herleitung dieser Beziehung wird zunächst der Quantisierungsschritt q des A/D-Umsetzers bestimmt. Bei reinen Wechselgrößen entspricht die Vollaussteuerung der doppelten Amplitude A. Bei einem Umsetzer mit N-Bit Auflösung ergibt sich somit ein Quantisierungsschritt zu
Der Quantisierungsfehler pro Schritt wird als gleichmäßig verteilt über das Intervall von -q/2 bis +q/2 angenommen. Damit ist die Leistungsdichte (Varianz) zufolge der Quantisierung gegeben als:
Sigma drückt das „Störsignal“ der Quantisierung aus, welches das Rauschen verursacht. Das sinusförmige Eingangssignal mit Vollpegel hat eine mittlere Leistung von:
Das Verhältnis aus PA und σ2 entspricht dem Signal-Rausch-Verhältnis. Nach Eliminierung von p aus den Gleichungen kommt man zu folgender bekannten Gleichung:
Somit hätte ein 16-bit A/D-Umsetzer bei sinusförmigem Eingangssignal und Vollpegel einen Signal-Rausch-Abstand von 98,1 dB. Wesentlich ist, dass diese Berechnung nur unter den oben genannten Voraussetzungen gültige Ergebnisse liefert und diese Gleichung keine allgemein gültige Lösung zum Berechnen des Quantisierungsrauschens darstellt. Bei A/D-Umsetzern mit nichtlinearer Kennlinie, wie sie beispielsweise bei dem A-law-Verfahren im Bereich der Telekommunikation eingesetzt werden, gilt aufgrund der nichtlinearen Übertragungsfunktion die hergeleitete Beziehung des Quantisierungsrauschens nicht.
Quantisierungsrauschen bei nicht sinusförmigen Signalen
Soll das Quantisierungsrauschen nicht nur bei sinusförmigen Signalen ermittelt werden, lässt sich für beliebige, stationäre Signale und bei linearem A/D-Umsetzer auch folgende, verallgemeinerte Berechnung für das Quantisierungsrauschen bei Vollpegel ermitteln:
Dabei stellt Apeak den Spitzenwert des Nutzsignals und Aeff den Effektivwert dar. Bei einem sinusförmigen Signal ist die Beziehung zwischen Spitzenwert und Effektivwert
 was nach Einsetzen auf obige Gleichung führt.
was nach Einsetzen auf obige Gleichung führt.Bei typischen Audiosignalen wie Musik und Sprache kann mit einem Faktor von rund 4 als Relation zwischen Spitzenwert und Effektivwert in guter Näherung gerechnet werden. Damit ist bei sonst gleichen Parametern der Signal-Rausch-Abstand zufolge des Quantisierungsrauschen bei einem Sprachsignal um etwa 9 dB schlechter als bei einem rein sinusförmigen Signal.
Beispiele
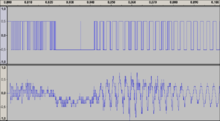
Das Diagramm zeigt den Amplitudenverlauf zweier Signale, die durch Quantisieren des Signals 8, (8 Bit Abtastung) entstanden. Das untere wurde mit 4 Bits quantisiert (Signal 4), entsprechend 16 unterschiedlichen Werten. Für das obere Signal (Signal 1) stand ein Bit mit entsprechend 2 verschiedenen Amplitudenwerten zur Verfügung.
Der Abstand zwischen Nutzsignalleistung und Rauschleistung bei 1-Bit-Quantisierung beträgt fast 8 dB. Es liegt oberhalb der Rauschschwelle, die für Sprachverständlichkeit erforderlich ist. Auch bei einer Abtastung mit nur zwei verschiedenen Amplitudenwerten bleibt Sprache verständlich. Selbst Lautstärkemodulationen bleiben erkennbar.
Klangbeispiele:
- Signal mit 8 Bit Abtastung, ca. 50 dB Signal-Rausch-Abstand:
- Signal mit 4 Bit, ca. 25 dB:
- Signal 1 mit 1 Bit, ca 8 dB:
Literatur
- Alan V. Oppenheim, Ronald W. Schafer: Zeitdiskrete Signalverarbeitung. 3. durchgesehene Auflage. Oldenbourg Verlag, München u. a. 1999, ISBN 3-486-24145-1.
Wikimedia Foundation.