Simpsonregel

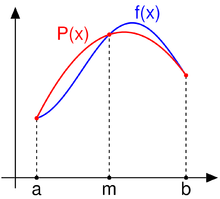
Die Simpsonregel oder Simpson'sche Formel (nach Thomas Simpson), manchmal auch Kepler'sche Fassregel (nach Johannes Kepler) ist ein Verfahren der numerischen Integration, bei dem eine Näherung zum Integral einer Funktion f(x) im Intervall [a,b] berechnet wird, indem man sie durch eine Parabel annähert.

Simpsonsche Formel

Die Parabel wird als Interpolationspolynom durch Funktionswerte an den Stellen $a, b, m=\tfrac{(a+b)}2$ gelegt. Das Integral nähert man dann durch das Integral der Parabel an. Die Simpsonregel ist damit eine sogenannte abgeschlossene Newton-Cotes-Formel. Damit ergibt sich dann

$Q(f) = \frac{b-a}{6} \cdot \left( f(a)+4f \left( \frac{a+b}{2} \right)+f(b) \right).$

Geschichte

Die Formel wurde erstmals benutzt von Evangelista Torricelli, ist aber benannt nach dem englischen Mathematiker Thomas Simpson. Sie entspricht der Keplerschen Fassregel, die Johannes Kepler bereits 1615 aufstellte.

Über die Entstehungsgeschichte berichtet Kepler in der Widmung der späteren Veröffentlichung. Nachdem 1611 Keplers erste Frau in Prag gestorben war, heiratete er – nun in Linz arbeitend – 1613 wieder. Er kaufte für die Hochzeit einige Fässer Wein. Als der Wein eingekellert war, kam der Verkäufer mit einer Messrute und bestimmte den Inhalt für alle Fässer ohne Überlegung oder Rechnung nach der gleichen Methode. Die Messrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden eingeführt und die Marke am Spundloch ergab den Rauminhalt. Kepler wunderte sich, dass eine Diagonale durch die Fasshälfte ein Maß für den Rauminhalt abgeben sollte und bezweifelte die Richtigkeit dieser Methode, da ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Rauminhalt die gleiche Visierlänge besitzen könnte.

Kepler verfasste daraufhin die Schrift Nova Stereometria doliorum vinariorum 1615 (Neue Inhaltsberechnung von Weinfässern), in der er nach überprüfbaren Methoden zur Inhaltsberechnung von Weinfässern suchte. Eine dieser Methoden bestand darin, die Krümmung des Fasses durch eine Parabel anzunähern, da Inhaltsberechnungen mit Hilfe von Parabeln seit Archimedes exakt durchgeführt werden konnten.

Unter anderem beschrieb er darin eine Formel zur Berechnung der Kapazität (genauer des Volumens) von Weinfässern mit unregelmäßigen Formen. Diese Formel liefert exakte Werte für den Pyramidenstumpf (einschließlich Pyramide), Kugel, elliptisches Paraboloid, einschaliges Hyperboloid und alle anderen Körperschichten, die sich durch ebene Körperschnitte senkrecht zu den Körperachsen erzeugen lassen.

Fehlerabschätzung

Ist f(x) viermal stetig differenzierbar in [a,b], dann gilt für den Fehler E(f) die Abschätzung

$\left| E(f) \right| \le \frac{(b-a)^5}{2880} \max_{a\le x \le b} {\left| f^{(4)}(x) \right|}.$

Ist f(x) zusätzlich noch reellwertig, dann gilt mit einer Zwischenstelle ζ aus [a,b] für das Restglied

$E(f) = - \frac{(b-a)^5}{2880}{{f^{(4)}(\zeta)}}.$

Diese Restglieddarstellung wurde 1887 von Giuseppe Peano gefunden. Sie besagt insbesondere, dass die Simpsonregel Polynome vom Grad drei exakt integriert, also einen Grad höher als man nach Konstruktion erwarten würde. Diese Eigenschaft haben alle abgeschlossenen Newton-Cotes-Formeln von geradem Grad.

Summierte simpsonsche Formel

Um das Integral noch besser annähern zu können unterteilt man das Intervall [a,b] in N nebeneinanderliegende, gleich große Teilintervalle der Länge h. In jedem Teilintervall wendet man die simpsonsche Formel für die einzelnen Teilflächen an und addiert danach die entstandenen Näherungen. Damit erhält man die summierte oder zusammengesetzte Simpsonregel

$Q(f)=\frac h6 \cdot \left( f(x_0) + 4 \cdot f \left( \frac{x_{0}+x_1}2 \right) + 2 \cdot f(x_1) + 4 \cdot f \left( \frac{x_{1}+x_2}2 \right)+ \dots + 2 \cdot f(x_{N-1}) + 4 \cdot f \left( \frac{x_{N-1}+x_N}2 \right) + f(x_{N})\right)$

bzw.

$Q(f)=\frac h3 \cdot \left( \frac 12 f(x_0)+\sum_{k=1}^{N-1}f(x_k)+2\sum_{k=1}^{N}f \left( \frac{x_{k-1}+x_k}2 \right)+\frac 12 f(x_N) \right)$

mit $h = \frac{b-a}{N}, \ x_k=a+k\cdot h.$

Man sieht leicht einen Zusammenhang mit der Sehnentrapezformel Q_S(f) und der Tangententrapezformel Q_T(f):

$Q(f)=\frac 13 \Big( Q_S(f)+2Q_T(f) \Big).$

Die Fehlerabschätzung für das Restglied lautet nun

$\left| E(f) \right| \le \frac{(b-a)}{2880}h^4 \max_{a\le x \le b} {\left| f^{(4)}(x) \right|}$

beziehungsweise für reellwertige Funktionen mit einer Zwischenstelle ζ aus dem Intervall [a,b]

$E(f)=-\frac{(b-a)}{2880}h^4f^{(4)}(\zeta).$

Alternative Formulierung

Alternativ kann man die Simpsonsformel auch auf jeweils zwei Teilintervalle anwenden (bei geradem N).

$Q(f)=\frac{h}{3}\left( f(x_0)+4\cdot f(x_1)+2\cdot f(x_2)+4\cdot f(x_3)+2\cdot f(x_4)+\dots +4\cdot f(x_{N-1})+f(x_N)\right).$

bzw.

$Q(f)= \frac{h}{3}\left( f(x_0)+ 2 \sum_{k=1}^{N/2-1}f(x_{2k})+ 4\sum_{k=1}^{N/2}f(x_{2k-1})+f(x_N) \right)$

mit $h = \frac{b-a}{N}, \ x_k=a+k\cdot h.$

Volumenberechnung

Der Name Fassregel lässt sich durch die folgende Anwendung begründen: Zur Berechnung des Volumens eines Weinfasses sei q(x) die Querschnittsfläche quer zur Längsachse in der Entfernung x vom Boden des Fasses; sie lässt sich durch Bestimmung des Umfanges leicht ausrechnen. Ist h die Höhe des Fasses, so ist das Volumen gleich

$V = \int_0^h q(x)\,\mathrm dx.$

Die Keplersche Fassregel gibt nun

$V = \frac{h}{6} \cdot \left(q(0) + 4q \left( \frac{h}{2} \right) + q(h)\right)$

als Näherungswert für das Volumen eines Körpers, dessen Querschnitt an drei Stellen bekannt ist. Ist der Körper ein Rotationskörper, so gilt bei Rotation um die x-Achse:

$\begin{align} V &= \pi \cdot \int_a^b (f(x))^2 \mathrm{d}x\\ &\approx \pi \frac{b-a}{6} \cdot \left(\left(f(a)\right)^2 + 4\left(f \left( \frac{a+b}{2} \right)\right)^2 + (f(b))^2\right) \end{align}$

Für bestimmte Rotationskörper wie Kegel und Kegelstumpf, Zylinder und Rotationsparaboloid gibt diese Formel das genaue Volumen an.

Ist u der Umfang von Boden und Deckel und U der Umfang in der Mitte des Fasses, so ergibt sich daraus die Näherungsformel:

$\frac{h}{6}\cdot \left[ 2\pi \left( {\frac{u}{2\pi}} \right)^2 + 4 \left( {\frac{U}{2\pi}} \right)^2 \pi \right] \ = \ \frac{h}{6}\cdot \left[ 2\pi \left( \frac{u^2}{4\pi^2} \right) + 4 \left( \frac{U^2}{4\pi^2} \right) \pi \right]=\frac h{12\pi}\cdot \left[u^2 + 2U^2\right].$

Der genaue Wert für eine parabolische Krümmung der Fassdauben ist

$\frac{h}{60\pi}\cdot \left[3u^2 + 4Uu + 8 U^2 \right].$

Verwendung als Runge-Kutta-Verfahren

Die Simpsonregel lässt sich auch als Runge-Kutta-Verfahren darstellen, und zwar mit dem Butcher-Schema

$\begin{array}{c|ccc} 0 & 0 & 0 & 0\\ \frac{1}{2} & \frac{1}{2} & 0 & 0\\ 1 & -1 & 2 & 0\\ \hline & \frac{1}{6} & \frac{4}{6} & \frac{1}{6} \end{array}.$

Literatur

• Hans R. Schwarz, Norbert Köckler: Numerische Mathematik. 6. Auflage, Teubner, Stuttgart 2006, ISBN 3-519-42960-8, S. 311-316.
• Johannes Kepler: Neue Stereometrie der Fässer. Aus dem Lateinischen übersetzt und herausgegeben von R. Klug. W. Engelmann. Leipzig, 1908.

Weblinks

• Website des Museumsraum zu Johannes Kepler des Bundesrealgymnasium Kepler, Graz