- Stochastische Konvergenz
-
In der Stochastik existieren verschiedene Konzepte eines Grenzwertbegriffs für Zufallsvariablen. Anders als im Fall reeller Zahlenfolgen gibt es keine natürliche Definition für das Grenzverhalten von Zufallsvariablen bei wachsendem Stichprobenumfang, weil das asymptotische Verhalten der Experimente immer von den einzelnen Realisationen abhängt und wir es also formal mit der Konvergenz von Funktionen zu tun haben. Daher haben sich im Laufe der Zeit unterschiedlich starke Konzepte herausgebildet, die wichtigsten dieser Konvergenzarten werden im folgenden kurz vorgestellt.
Inhaltsverzeichnis
Voraussetzungen
Wir werden die klassischen Konvergenzbegriffe immer im folgenden Modell formulieren: Gegeben sei eine Folge
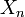 von Zufallsvariablen, die auf einem Wahrscheinlichkeitsraum (Ω,Σ,P) definiert ist. Eine Realisation dieser Folge wird üblicherweise mit
von Zufallsvariablen, die auf einem Wahrscheinlichkeitsraum (Ω,Σ,P) definiert ist. Eine Realisation dieser Folge wird üblicherweise mit 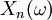 bezeichnet.
bezeichnet.Fast sichere Konvergenz
Der Begriff der fast sicheren Konvergenz ist am ehesten mit der Formulierung für Zahlenfolgen vergleichbar. Er wird vor allem bei der Formulierung von starken Gesetzen der großen Zahlen verwendet.
Man sagt, dass die Folge Xn fast sicher gegen eine Zufallsvariable X konvergiert, falls
gilt. Übersetzt bedeutet dies, dass für fast alle Realisationen der Folge der klassische Konvergenzbegriff aus der reellen Analysis gilt.
Schreibweise:
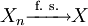 .
.Die fast sichere Konvegenz ist äquivalent zur punktweisen Konvergenz fast überall aus der Maßtheorie.
Konvergenz im p-ten Mittel
Ein integrationstheoretischer Ansatz wird mit dem Begriff der Konvergenz im p-ten Mittel verfolgt. Es werden dabei nicht einzelne Realisationen betrachtet, sondern Erwartungswerte der Zufallsvariablen.
Formal konvergiert
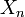 im p-ten Mittel gegen eine Zufallsvariable X, falls
im p-ten Mittel gegen eine Zufallsvariable X, fallsgilt. Dabei wird
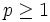 vorausgesetzt. Dies bedeutet, dass die Differenz
vorausgesetzt. Dies bedeutet, dass die Differenz 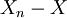 im Lp-Raum
im Lp-Raum 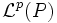 gegen 0 konvergiert. Man bezeichnet diese Konvergenz daher auch als
gegen 0 konvergiert. Man bezeichnet diese Konvergenz daher auch als 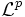 - Konvergenz.
- Konvergenz.Wegen der Ungleichung der verallgemeinerten Mittelwerte folgt für
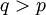 aus der Konvergenz im q-ten Mittel die Konvergenz im p-ten Mittel.
aus der Konvergenz im q-ten Mittel die Konvergenz im p-ten Mittel.Stochastische Konvergenz
Ein etwas schwächerer Konvergenzbegriff ist die stochastische Konvergenz oder Konvergenz in Wahrscheinlichkeit. Wie der Name bereits suggeriert, werden nicht spezielle Realisationen der Zufallsvariablen betrachtet, sondern Wahrscheinlichkeiten für bestimmte Ereignisse. Eine klassische Anwendung der stochastischen Konvergenz sind schwache Gesetze der großen Zahlen.
Die mathematische Formulierung lautet: Die Folge
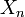 konvergiert stochastisch gegen eine Zufallsvariable X, falls
konvergiert stochastisch gegen eine Zufallsvariable X, fallsdas heißt, die Wahrscheinlichkeit, dass der Abstand zwischen der beobachteten und der theoretischen Größe größer ist als jedes positive (insbesondere: jedes beliebig nahe an null liegende positive) ε, geht gegen null, wenn die Anzahl der Realisationen gegen unendlich geht.
Kürzere Schreibweisen:
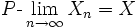 oder
oder 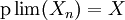 oder
oder 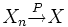 .
.Man kann zeigen, dass eine Folge
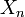 genau dann stochastisch gegen X konvergiert, falls
genau dann stochastisch gegen X konvergiert, fallsd.h. die stochastische Konvergenz entspricht der Konvergenz bezüglich einer Metrik. Der Raum aller Zufallsvariablen versehen mit dieser Metrik bildet einen topologischen Vektorraum, der im Allgemeinen nicht lokal konvex ist.
Die stochastische Konvergenz entspricht der Konvergenz dem Maße nach aus der Maßtheorie.
Schwache Konvergenz
Der vierte prominente Konvergenzbegriff ist der der schwachen Konvergenz (für Maße) oder Konvergenz in Verteilung (für Zufallsvariablen).
Definition für Maße
Sei (Ω,d) ein metrischer Raum und Σ die dazugehörige Borelsche σ-Algebra. Eine Folge μn von endlichen Maßen auf dem Messraum (Ω,Σ) konvergiert schwach gegen ein Maß μ, falls für alle beschränkten und bzgl. (Ω,d) stetigen Funktionen
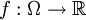
gilt.[1]
Anwendung auf Zufallsvariablen
Eine Folge von Zufallsvariablen
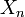 konvergiert in Verteilung gegen die Zufallsvariable X, wenn die Folge der induzierten Bildmaße
konvergiert in Verteilung gegen die Zufallsvariable X, wenn die Folge der induzierten Bildmaße 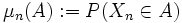 schwach gegen das Bildmaß
schwach gegen das Bildmaß 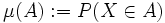 konvergiert. Äquivalent dazu ist die Charakterisierung, dass für die Verteilungsfunktionen
konvergiert. Äquivalent dazu ist die Charakterisierung, dass für die Verteilungsfunktionen 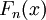 von
von 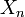 und
und 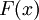 von
von 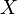
punktweise in allen Stetigkeitspunkten von
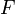 gilt [2]. Die wohl bekanntesten Anwendungen der Konvergenz in Verteilung sind zentrale Grenzwertsätze.
gilt [2]. Die wohl bekanntesten Anwendungen der Konvergenz in Verteilung sind zentrale Grenzwertsätze.Da die Konvergenz in Verteilung ausschließlich durch die Bildmaße bzw. durch die Verteilungsfunktion der Zufallsvariablen definiert sind, ist es nicht notwendig, dass die Zufallsvariablen auf demselben Wahrscheinlichkeitsraum definiert sind.
Als Notation verwendet man in der Regel
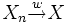 oder
oder 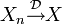 . Die Buchstaben „W“ bzw. „D“ stehen dabei für die entsprechenden Begriffe im Englischen, also weak convergence bzw. convergence in distribution.
. Die Buchstaben „W“ bzw. „D“ stehen dabei für die entsprechenden Begriffe im Englischen, also weak convergence bzw. convergence in distribution.Zusammenhang mit charakteristischen Funktionen
Zwischen der punktweisen Konvergenz der charakteristischen Funktion
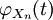 einer Folge von Zufallsvariablen Xn und der schwachen Konvergenz von Xn besteht folgender Zusammenhang:
einer Folge von Zufallsvariablen Xn und der schwachen Konvergenz von Xn besteht folgender Zusammenhang: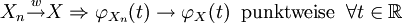
Für die Gegenrichtung ist noch die Stetigkeit der Grenzfunktion im Nullpunkt nachzuweisen:
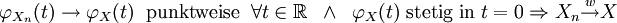
Oftmals ist der Nachweis der punktweisen Konvergenz der charakteristischen Funktion einfacher als der direkte Nachweis der Konvergenz der Verteilungsfunktionen. Mit der Eindeutigkeit der charakteristischen Funktion lässt sich so auch der Grenzwert der Zufallsvariable Xn bestimmen.
Zusammenhang zwischen den einzelnen Konvergenzarten
In der Reihe der wichtigsten Konvergenzbegriffe in der Stochastik stellen die beiden zuerst vorgestellten Begriffe die stärksten Konvergenzarten dar. Sowohl aus fast sicherer Konvergenz [3] als auch aus Konvergenz im p-ten Mittel[4] lässt sich immer die stochastische Konvergenz einer Folge von Zufallsvariablen ableiten. Ferner folgt aus stochastischer Konvergenz automatisch auch die Konvergenz in Verteilung, die die schwächste der hier vorgestellten Konvergenzarten ist.[5]
In Ausnahmefällen gelten auch noch andere Implikationen: Wenn eine Folge von Zufallsvariablen in Verteilung gegen eine Zufallsvariable X konvergiert und X fast sicher konstant ist, dann konvergiert diese Folge auch stochastisch.
Aus der Konvergenz im p-ten Mittel folgt im Allgemeinen nicht die fast sichere Konvergenz. Es gilt bei Konvergenz im p-ten Mittel aber immer, dass es eine Teilfolge gibt, die fast sicher konvergiert.
Umgekehrt lässt sich aus fast sicherer Konvergenz im Allgemeinen auch keine Konvergenz im p-ten Mittel schließen. Allerdings ist dieser Schluss erlaubt, wenn es eine gemeinsame Majorante in Lp gibt (siehe Satz von der majorisierten Konvergenz)
Beispiel
Auf dem Wahrscheinlichkeitsraum (Ω,Σ,P) mit Ω = [0,1], Σ den Borelmengen und P dem Lebesgue-Maß betrachte man die Zufallsvariable X(ω) = 0 sowie die Folge Xn(ω) der Zufallsvariablen, die für n = 2k + m mit
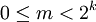 (jedes natürliche n besitzt eine eindeutige Zerlegung dieser Art) folgendermaßen definiert ist[6][7]:
(jedes natürliche n besitzt eine eindeutige Zerlegung dieser Art) folgendermaßen definiert ist[6][7]:Wegen
konvergiert Xn im p-ten Mittel gegen X. Aus dem oben beschriebenen Zusammenhang zwischen den einzelnen Konvergenzarten folgt, dass Xn ebenso stochastisch gegen X konvergiert, wie sich auch aus
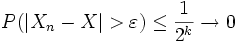 für jedes
für jedes 
erkennen lässt.
Die Funktionen Xn sind sozusagen immer dünner werdende Zacken, die über das Intervall [0,1] laufen. Für jedes fixe
![\omega\in [0,1]](/pictures/dewiki/54/60df83412e28b00fbf28ff8c96609d5f.png) gilt aber Xn(ω) = 1 für unendliche viele n, ebenso ist Xn(ω) = 0 für unendlich viele n, sodass also keine fast sichere Konvergenz von Xn vorliegt.
gilt aber Xn(ω) = 1 für unendliche viele n, ebenso ist Xn(ω) = 0 für unendlich viele n, sodass also keine fast sichere Konvergenz von Xn vorliegt.Zu jeder Teilfolge
 von Xn lässt sich allerdings eine Teilteilfolge
von Xn lässt sich allerdings eine Teilteilfolge  finden, die gegen X konvergiert. Gäbe es eine Topologie der fast sicheren Konvergenz, so würde aus dieser Eigenschaft folgen, dass Xn fast sicher gegen X konvergiert. Dieses Beispiel zeigt also auch, dass es keine Topologie der fast sicheren Konvergenz geben kann.[8]
finden, die gegen X konvergiert. Gäbe es eine Topologie der fast sicheren Konvergenz, so würde aus dieser Eigenschaft folgen, dass Xn fast sicher gegen X konvergiert. Dieses Beispiel zeigt also auch, dass es keine Topologie der fast sicheren Konvergenz geben kann.[8]Einzelnachweise
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Chapter 4.5
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 4.5.4
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 2.5.5
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Theorem 2.5.1
- ↑ Virtual Laboratories in Probability and Statistics, Excercise 3.8.3
- ↑ Robert B. Ash: Real Analysis and Probability. Academic Press, New York 1972. ISBN 0-12-065201-3. Examples 2.5.6
- ↑ Bernard R. Gelbaum, John M.H. Olmsted: Counterexamples in Analysis. Dover Publications, ISBN 0-486-42875-3. 40. Sequences of functions converging in different senses. p 109ff
- ↑ J. Cigler, H.-C. Reichel: Topologie. Eine Grundvorlesung. Bibliographisches Institut, Mannheim 1978, ISBN 3-411-00121-6, S. 88, Aufgabe 6.
Literatur
- Heinz Bauer: Wahrscheinlickeitstheorie. 4 Auflage. De Gruyter, Berlin 1991, ISBN 3110121905, S. 34 (Konvergenz von Zufallsvariablen und Verteilungen).
- Heinz Bauer: Maß- und Integrationstheorie. 2. Auflage, De Gruyter, Berlin 1992, ISBN 3-11-013625-2, ab S.91 (§15 Konvergenzsätze) und ab S.128 (§20 Stochastische Konvergenz).
- Jürgen Elstrodt: Maß- und Integrationstheorie. 4. Auflage, Springer, Berlin 2005, ISBN 3-540-21390-2, (beschreibt ausführlich die Zusammenhänge zwischen den verschiedennen Konvergenzarten).
Siehe auch
Wikimedia Foundation.

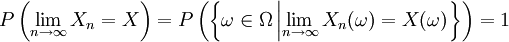
![\lim_{n \rightarrow \infty} E[|X_n - X|^p] = 0](/pictures/dewiki/48/0eefddaccfcce7f92a169d86fd796f74.png)
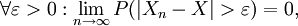
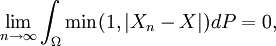
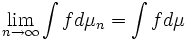
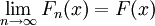
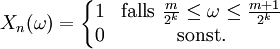
![E[|X_n - X|^p] = \int_0^1 |X_n(\omega)-0|^p d\omega = \frac{1}{2^k}\to 0](/pictures/dewiki/99/ca3c62719815f77292a7b4f52021c41a.png)