Stoßmittelpunkt

Bei einem physikalischen Pendel oder Trägheitspendel handelt es sich um ein theoretisches Modell zur Beschreibung der Schwingung eines realen Pendels. Im Gegensatz zum mathematischen Pendel werden hierbei Form und Größe des Körpers berücksichtigt, wodurch das Verhalten physikalischer Pendel eher dem realer Pendel entspricht.

Das physikalische Pendel besteht aus einem ausgedehnten, starren Körper, welcher nicht in seinem Massenmittelpunkt (siehe auch Schwerpunkt) aufgehängt im Schwerefeld nach einer Auslenkung aus seiner Gleichgewichtslage schwingt. Nicht berücksichtigt werden zugunsten der Lösbarkeit Reibungskraft sowie größere Amplituden.

Die Schwingungsdauer des physikalischen Pendels ergibt sich (Herleitung mittels des Drehmoments siehe unten) zu $T = \frac {2 \pi} {\omega} = 2 \pi \sqrt{\frac {I} {mgd}}$,

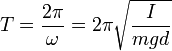wobei ω die Kreisfrequenz, I das Trägheitsmoment bzgl. des Aufhängepunktes, m die Masse des Körpers, g die Schwerebeschleunigung und d der Abstand vom Aufhängungspunkt zum Massenmittelpunkt ist.

Reduzierte Pendellänge

Unter der reduzierten Pendellänge versteht man die Länge 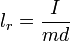$l_r = \frac {I} {md}$, äquivalent der Länge l in der Schwingungsgleichung des mathematischen Pendels gleicher Schwingungsdauer. Gleichzeitig wird über diese Größe der Schwingungs- oder Stoßmittelpunkt festgelegt. Dieser nicht mit dem Schwerpunkt des Pendels zu verwechselnde Ort hat die Eigenschaft, dass ein dort hin gerichteter Stoß keinerlei Lagerreaktion im Aufhängungspunkt des Pendels erzeugt. Des weiteren ändert sich die Schwingungsdauer eines physikalischen Pendels nicht, wenn Aufhängepunkt und Schwingungsmittelpunkt vertauscht werden (siehe auch Reversionspendel).

Mathematische Beschreibung

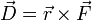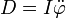Zur Berechnung der Schwingungsdauer bedient man sich zweier unterschiedlicher Ansätze für das auf das physikalische Pendel wirkende Drehmoment, $\vec D = \vec r \times \vec F$ und $D = I \ddot {\varphi}$, die sich auch beim mathematischen Pendel anwenden lassen.

Bei Annahme einer Schwingung des im Ursprung aufgehängten Pendelkörpers auf der x-y-Ebene lässt sich der Schwerpunkt des Körpers im Ruhezustand durch 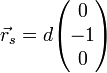$\vec r_s = d \begin{pmatrix} 0 \\ -1 \\ 0 \end{pmatrix}$, im um 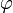${\varphi}$ ausgelenkten Zustand durch 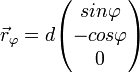$\vec r_{\varphi} = d \begin{pmatrix} sin {\varphi} \\ - cos {\varphi} \\ 0 \end{pmatrix}$ beschreiben. Nun lässt sich das auf das physikalische Pendel wirkende Drehmoment wie für eine im Schwerpunkt des Pendels liegende Punktmasse gleicher Masse berechnen: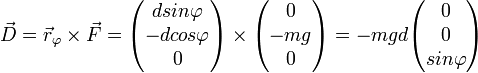 $\vec D= \vec r_{\varphi} \times \vec F = \begin{pmatrix} d sin {\varphi} \\ - d cos {\varphi} \\ 0 \end{pmatrix} \times \begin{pmatrix}0 \\ -m g\\ 0 \end{pmatrix}= -m g d \begin{pmatrix}0 \\ 0 \\ sin {\varphi} \end{pmatrix}$

Man sieht nun, dass das auf das Pendel wirkende Drehmoment nur eine Komponente 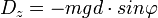$D_z= -m g d \cdot sin {\varphi}$ in z-Richtung hat, es also normal auf die Schwingungsebene steht.

Durch Gleichsetzen mit dem Ansatz 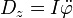$D_z= I \ddot {\varphi}$ (Drehmoment eines ausgedehnten Körpers) und anschließendes Umformen erhält man die Gleichung 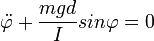$\ddot {\varphi} + \frac {m g d} {I} sin {\varphi} = 0$, wobei sich der Sinus für kleine Winkel mit 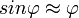$sin {\varphi} \approx {\varphi}$ approximieren lässt. Die Gleichung 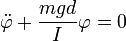$\ddot {\varphi} + \frac {m g d} {I} {\varphi} = 0$ beschreibt eine harmonische Schwingung mit 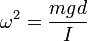${\omega}^2 = \frac {m g d} {I}$, die Schwingungsdauer des Pendels beträgt $T = \frac {2 \pi} {\omega} = 2 \pi \sqrt{\frac {I} {m g d}}$.

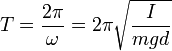Siehe auch

• Pendel
• Mathematisches Pendel
• Foucaultsches Pendel
• Fadenpendel
• Doppelpendel
• Magnetisches Pendel
• Pendeluhr
• Sekundenpendel