- Mathematisches Pendel
-
Ein mathematisches Pendel ist eine Idealisierung des realen Pendels. Es ist ein grundlegendes Modell zum Verständnis von Pendelschwingungen.
Mathematische Pendel sind durch zwei wesentliche Eigenschaften charakterisiert:
- Es herrscht keine Reibung in irgendeiner Form, also weder Strömungswiderstand noch innere Reibung in Faden oder Aufhängepunkt.
- Die gesamte Masse des Pendels ist in einem einzigen Punkt konzentriert. Der Faden wird als masselos betrachtet, die Massenverteilung des Pendelkörpers wird durch ihren Massenmittelpunkt dargestellt.
In der Praxis kann man ein mathematisches Pendel dadurch annähern, dass man einen möglichst langen und dünnen Faden und einen möglichst kleinen und schweren Pendelkörper verwendet. Da die maximale Auslenkung in dieser Konfiguration nur nach einer langen Beobachtungszeit zurückgeht, herrscht ein weitgehend reibungsfreier Zustand.
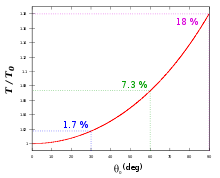
Bei kleiner Auslenkung hängt die Frequenz der Pendelschwingung ausschließlich von der Länge des Pendels und der Fallbeschleunigung ab. Größere Auslenkungswinkel beeinflussen aber zunehmend die Pendelfrequenz.
Anders als man zunächst vermuten könnte, spielt die Masse des Pendels keine Rolle.
Inhaltsverzeichnis
Mathematische Beschreibung
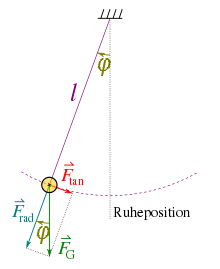
Anhand der Kräfte wird im folgenden die Bewegungsgleichung der Pendelschwingung ermittelt.
Aufgrund der Schwerkraft (g = Ortsfaktor) ergibt sich bei Auslenkung eines Fadenpendels der Masse m eine Kraft FR(t), die tangential zur kreisförmigen Pendelbahn wirkt. Diese Rückstellkraft steigt mit dem Auslenkungswinkel φ bezüglich der Ruhelage.
Beim Betrachten eines schwingenden Fadenpendels zeigt sich, dass die Geschwindigkeit mit zunehmender Auslenkung abnimmt und nach Erreichen des Scheitelpunkts die Richtung wechselt. Die Geschwindigkeitsänderung bedeutet, dass die Pendelmasse eine Beschleunigung erfährt, genauer gesagt findet eine Tangentialbeschleunigung statt, da eine kreisförmige Bewegungsbahn vorliegt. Dabei setzt das 2. Newtonsche Gesetz eine der Beschleunigung proportionale Kraft voraus.
Durch den Zusammenhang aus Tangentialbeschleunigung und Winkelbeschleunigung lässt sich die erforderliche Beschleunigungskraft auf eine Zeitgleichung des Auslenkungswinkels überführen.
Da bei der ungestörten Schwingung die Rückstellkraft des Pendels die einzige aktive Kraft darstellt, können die beiden Kraftgleichungen gleichgesetzt werden. Woraus nach Umstellen und Kürzen eine nichtlineare Differenzialgleichung zweiter Ordnung entsteht.
- Fa(t) = FR(t)


Für kleine Winkel gilt die Kleinwinkelnäherung:
 .
.
Durch Substitution ergibt sich somit eine lineare Differenzialgleichung zweiter Ordnung, deren allgemeine Lösung zur Schwingungsgleichung führt.
Hierbei bezeichnen
 die Winkelamplitude und φ0 den Nullphasenwinkel zum Zeitpunkt t = 0. Darüber hinaus sind die Eigenkreisfrequenz ω0 und die zugehörige Periodendauer T ersichtlich.
die Winkelamplitude und φ0 den Nullphasenwinkel zum Zeitpunkt t = 0. Darüber hinaus sind die Eigenkreisfrequenz ω0 und die zugehörige Periodendauer T ersichtlich.Alternativ lässt sich die Periodendauer, ohne den Proportionalitätsfaktor 2π, auch mit dem Buckinghamschen Π-Theorem herleiten.
Exakte Lösung
Da Pendel in der Realität immer mehr als infinitesimal ausgelenkt werden, verhalten sie sich nichtlinear. Die allgemeine Differentialgleichung ist elementar nicht lösbar und erfordert Kenntnisse über elliptische Integrale. Damit lässt sich die allgemeine Lösung in eine Reihe entwickeln:
Alternativ lässt sich das auftretende elliptische Integral auch über das arithmetisch-geometrische Mittel M auswerten:
Außerdem ist die Dämpfung durch Reibungsverluste bei einem echten Pendel größer als Null, so dass die Auslenkungen ungefähr exponentiell mit der Zeit abnehmen.
Literatur
- Ekbert Hering, Rolf Martin, Martin Stohrer: Physik für Ingenieure. 8. Auflage. Springer, Berlin Heidelberg New York 2002, ISBN 3540429646.
Siehe auch
- physikalisches Pendel
- Foucaultsches Pendel
- Torsionspendel
- Gekoppelte Pendel
- Doppelpendel
- Multipendel
- Sekundenpendel
Weblinks
- Das Fadenpendel, Walter Bislin
- A comprehensive analytical solution of the nonlinear pendulum, Karlheinz Ochs
Wikimedia Foundation.