- Ungleichung der Mittelwerte
-
In der Mathematik besagt die Ungleichung vom arithmetischen und geometrischen Mittel, dass das arithmetische Mittel stets mindestens so groß wie das geometrische Mittel ist. Diese Ungleichung wurde vermutlich erstmals von Augustin Louis Cauchy 1821 bewiesen[1] und zählt zu den wichtigsten mathematischen Theoremen. Auf einer 1999 veröffentlichten Liste der 100 wichtigsten mathematischen Sätze[2] ist sie auf Platz 38 gereiht.
Inhaltsverzeichnis
Exakte Formulierung
Für ein n-Tupel
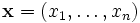 nichtnegativer Zahlen
nichtnegativer Zahlen 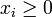 bezeichnet man in der Mathematik den Ausdruck
bezeichnet man in der Mathematik den Ausdruckals das arithmetische Mittel dieser Zahlen.
Der Ausdruck
wird als das geometrische Mittel dieser Zahlen bezeichnet.
Die Ungleichung vom arithmetischen und geometrischen Mittel besagt nun, dass das arithmetische Mittel stets mindestens so groß wie das geometrische Mittel ist:
 .
.
Gleichheit wird genau dann erreicht, wenn alle
 gleich sind.
gleich sind.Beweise
Für den Fall, dass ein
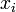 gleich Null ist, ist das geometrische Mittel Null und die Ungleichung ist offensichtlich erfüllt; in den folgenden Beweisen kann daher
gleich Null ist, ist das geometrische Mittel Null und die Ungleichung ist offensichtlich erfüllt; in den folgenden Beweisen kann daher 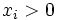 angenommen werden.
angenommen werden.Beweis aus der jensenschen Ungleichung
Die Ungleichung vom arithmetischen und geometrischen Mittel lässt sich beispielsweise aus der jensenschen Ungleichung beweisen: die Logarithmusfunktion ist konkav, daher gilt
Durch Anwendung der Exponentialfunktion auf beide Seiten folgt
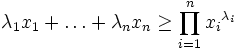 .
.
Für
 ergibt das genau die Ungleichung vom arithmetischen und geometrischen Mittel.
ergibt das genau die Ungleichung vom arithmetischen und geometrischen Mittel.Beweis von Polya
Von George Polya stammt ein Beweis, der lediglich die Beziehung
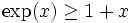 der Exponentialfunktion voraussetzt. Für
der Exponentialfunktion voraussetzt. Für  gilt dann
gilt dann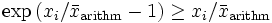 .
.
Multipliziert man diese Ungleichungen für
 , so erhält man
, so erhält man ,
,
also
und somit
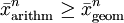 .
.
Induktive Beweise
Der Beweis aus der jensenschen Ungleichung und der Polya-Beweis sind zwar sehr leicht verständlich, hat aber den Nachteil, dass Vorwissen über die Logarithmusfunktion beziehungsweise der Exponentialfunktion benötigt wird. Für die Untersuchung der bei der Definition der Exponentialfunktion verwendeten Folge
kann aber die Ungleichung vom arithmetischen und geometrischen Mittel hilfreich sein. Methodisch sind daher oft induktive Beweise zweckmäßiger; diese sind für die Ungleichung vom arithmetischen und geometrischen Mittel aber relativ schwierig.
Beweis mit Vorwärts-Rückwärts-Induktion
Ein induktiver Beweis der Ungleichung vom arithmetischen und geometrischen Mittel ist mit „Vorwärts-Rückwärts-Induktion“ möglich. Der Vorwärtsschritt erfolgt dabei, indem man aus der Gültigkeit der Ungleichung für n die Gültigkeit für 2n beweist. Der Rückwärtsschritt erfolgt, indem man aus der Gültigkeit der Ungleichung für n die Gültigkeit für n−1 zeigt, indem man
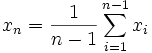 setzt. Dieser Beweis findet sich bereits bei Augustin Louis Cauchy, Cours d'analyse de l'Ecole Royale Polytechnique, premier partie, Analyse algebrique, Paris 1821, S. 457ff.
setzt. Dieser Beweis findet sich bereits bei Augustin Louis Cauchy, Cours d'analyse de l'Ecole Royale Polytechnique, premier partie, Analyse algebrique, Paris 1821, S. 457ff.Beweis mittels Hilfssatz
Ein anderer Beweis der Ungleichung vom arithmetischen und geometrischen Mittel ergibt sich aus dem Hilfssatz, dass für
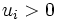 und
und  folgt, dass
folgt, dass 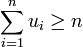 . Ein Beweis dieses Hilfssatzes findet sich im Artikel über vollständige Induktion. Betrachtet man das Produkt
. Ein Beweis dieses Hilfssatzes findet sich im Artikel über vollständige Induktion. Betrachtet man das Produkt  und setzt
und setzt ![u_i:=\frac{x_i}{\sqrt[n]{p}}](/pictures/dewiki/51/3bedfb036088d4f59bee3abfb51da5d9.png) , so erfüllen die so definierten
, so erfüllen die so definierten 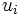 nämlich die Voraussetzung
nämlich die Voraussetzung  des Hilfssatzes. Aus dem Hilfssatz folgt
des Hilfssatzes. Aus dem Hilfssatz folgt![n\leq \sum_{i=1}^n u_i = \sum_{i=1}^n \frac{x_i}{\sqrt[n]{p}}](/pictures/dewiki/102/f27310da1f0a4595f69e027758bf6f37.png) ,
,
also
![\sqrt[n]{p} \leq \frac{1}{n}\sum_{i=1}^n x_i](/pictures/dewiki/54/660df6c4aa4c74100060013237a7070c.png) .
.
Einsetzen von
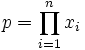 liefert dann die Ungleichung vom arithmetischen und geometrischen Mittel.
liefert dann die Ungleichung vom arithmetischen und geometrischen Mittel.Beweis aus Bernoulli-Ungleichung
Ein direkter induktiver Beweis ist mit Hilfe der bernoullischen Ungleichung möglich: Sei o.B.d.A. xn + 1 das maximale Element von
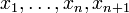 und
und 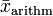 das arithmetische Mittel von
das arithmetische Mittel von 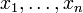 . Dann gilt
. Dann gilt 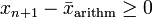 , und aus der bernoullischen Ungleichung folgt, dass
, und aus der bernoullischen Ungleichung folgt, dass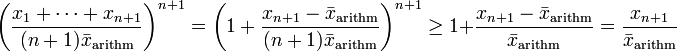 .
.
Mit der Induktionsvoraussetzung folgt dann
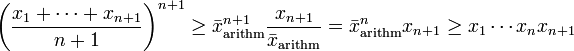 ,
,
also genau die Behauptung.
Dieser Beweis findet sich beispielsweise in H. Heuser, Lehrbuch der Analysis, Teil 1, Kapitel 12.2.
Beweis aus der Umordnungs-Ungleichung
Ein nicht-induktiver Beweis der Ungleichung vom arithmetischen und geometrischen Mittel, der ohne Logarithmusfunktion auskommt, lässt sich mit Hilfe der Umordnungs-Ungleichung durchführen. Aus der Umordnungs-Ungleichung folgt nämlich, dass für positive Zahlen
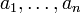 und jede beliebige Permutation
und jede beliebige Permutation  die Beziehung
die Beziehunggelten muss. Setzt man speziell
so folgt also
woraus unmittelbar die Ungleichung vom arithmetischen und geometrischen Mittel folgt.
Verallgemeinerungen
Ungleichung vom gewichteten arithmetischen und geometrischen Mittel
Für ein gegebenes positives Gewichtstupel
 mit wi > 0 und Summe
mit wi > 0 und Summe 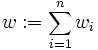 wird mit
wird mitdas gewichtete arithmetische Mittel und mit
![\bar{x}_{geom}=\sqrt[w]{\prod_{i=1}^n x_i^{w_i}}](/pictures/dewiki/51/3d7f123d8744ab3092b28a760796c6cd.png) ,
,
das gewichtete geometrische Mittel bezeichnet. Auch für diese gewichteten Mittel gilt die die Ungleichung
 .
.
Der Beweis dafür folgt direkt aus obigem Beweis mit der jensenschen Ungleichung.
Für n = 2,
 ,
,  mit
mit 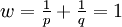 und x1 = ap, x2 = bq mit
und x1 = ap, x2 = bq mit 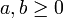 erhält man die Youngsche Ungleichung
erhält man die Youngsche UngleichungUngleichung vom harmonischen und geometrischen Mittel
Fordert man xi echt größer Null und ersetzt in der Ungleichung vom arithmetischen und geometrischen Mittel xi durch 1 / xi, so erhält man die Ungleichung vom harmonischen und geometrischen Mittel:
![\frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \leq \sqrt[n]{\prod_{i=1}^n{x_i}}](/pictures/dewiki/55/73279af778911ab838ab2bbbd4b98d18.png) .
.
Diese Ungleichung gilt ebenfalls für die gewichteten Mittel:
![\frac{w}{\sum_{i=1}^n \frac{w_i}{x_i}} \leq \sqrt[w]{\prod_{i=1}^n x_i^{w_i} }](/pictures/dewiki/98/b2b3fa5ea97d142575e55c4dfc501cf4.png) .
.
Ungleichung der verallgemeinerten Mittel
Als Hölder-Mittel mit Exponent k bezeichnet man den Ausdruck
![\bar{x}(k) = \sqrt[k]{\frac{1}{n}\sum_{i=1}^n{x_i^k}}](/pictures/dewiki/49/17f2edfaceb8c438be3fe865bd08aaa1.png) .
.
- Für
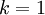 erhält man das arithmetische Mittel,
erhält man das arithmetische Mittel, - Der Grenzwert
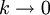 ergibt das geometrisches Mittel.
ergibt das geometrisches Mittel.
Allgemein gilt für
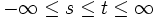 die verallgemeinerte Mittelwertungleichung:
die verallgemeinerte Mittelwertungleichung:Diese Ungleichung lässt sich z.B. beweisen, indem man
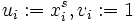 setzt und
setzt und 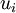 und
und 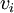 in die Hölder-Ungleichung mit
in die Hölder-Ungleichung mit 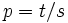 einsetzt, oder indem man die jensensche Ungleichung für die konvexe Funktion
einsetzt, oder indem man die jensensche Ungleichung für die konvexe Funktion 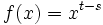 auf die Werte
auf die Werte  anwendet.
anwendet.Auch diese Ungleichung gilt ebenfalls für die gewichteten Mittel: Sei
das mit
 gewichtete Mittel mit Exponent k der Zahlen xi, so gilt für -∞ ≤ s ≤ t ≤ ∞ die Ungleichung:
gewichtete Mittel mit Exponent k der Zahlen xi, so gilt für -∞ ≤ s ≤ t ≤ ∞ die Ungleichung: .
.
Diese Ungleichung lässt sich ebenfalls aus der Hölder-Ungleichung beweisen, indem man
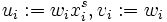 sowie
sowie 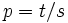 setzt, oder ebenfalls, indem man die jensensche Ungleichung für die konvexe Funktion
setzt, oder ebenfalls, indem man die jensensche Ungleichung für die konvexe Funktion 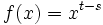 auf die Werte
auf die Werte  anwendet.
anwendet.Übertragen auf Integrale über den Maßraum
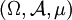 mit einem endlichen Maß
mit einem endlichen Maß 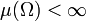 nimmt die Ungleichung der verallgemeinerten Mittel die Form
nimmt die Ungleichung der verallgemeinerten Mittel die Forman; insbesondere folgt daraus
 für die Lp-Räume
für die Lp-Räume 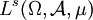 und
und 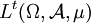 .
.Muirhead-Ungleichung
Eine andere Verallgemeinerung der Ungleichung vom arithmetischen und geometrischen Mittel ist die Muirhead-Ungleichung.
Anwendungen
Aus der Ungleichung vom arithmetischen und geometrischen Mittel lässt sich die Cauchy-Schwarz-Ungleichung ableiten.
Siehe auch
Einzelnachweise
- ↑ Cauchy, Augustin-Louis. Analyse algébrique. Der Beweis der Ungleichung vom arithmetischen und geometrischen Mittel ist auf Seite 457ff.
- ↑ The Hundred Greatest Theorems
Wikimedia Foundation.

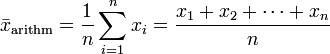
![\bar{x}_\mathrm{geom} = \sqrt[n]{\prod_{i=1}^n{x_i}}](/pictures/dewiki/48/0e3717a82a732acf4cde657e5be75afc.png)
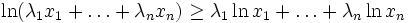
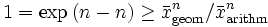
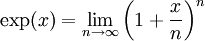
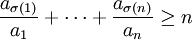
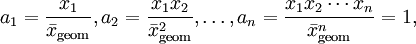
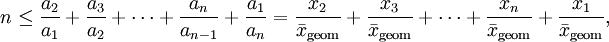

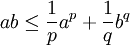
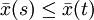
![\bar{x}(\mathbf{w},k) = \sqrt[k]{\frac{1}{w}\sum_{i=1}^n{w_i x_i^k}}](/pictures/dewiki/97/ac8ac54878f0b86bd7a831ee4a597b0b.png)
![\sqrt[s]{\frac{1}{\mu(\Omega)}\int_\Omega |f(x)|^s\,d\mu(x)}\leq \sqrt[t]{\frac{1}{\mu(\Omega)}\int_\Omega |f(x)|^t\,d\mu(x)}](/pictures/dewiki/57/91d0e94f3ebc05465af8219e1e3ad3ee.png)