- Borel-Unteralgebra
-
Lie-Algebra berührt die Spezialgebiete
ist Spezialfall von
Beispiele sind
- R3 mit Kreuzprodukt
- assoziative Algebra mit Kommutator
- glatte Vektorfelder auf einer glatten Mannigfaltigkeit
- spezielle lineare Lie-Algebra|sl(n,R)
Eine Lie-Algebra, benannt nach Sophus Lie, ist eine algebraische Struktur, die hauptsächlich zum Studium geometrischer Objekte wie Lie-Gruppen und differenzierbare Mannigfaltigkeiten eingesetzt wird.
Inhaltsverzeichnis
Definition
Eine Lie-Algebra ist ein Vektorraum
 über einem Körper K zusammen mit einer Verknüpfung
über einem Körper K zusammen mit einer Verknüpfung ![[\cdot,\cdot]:\mathfrak g\times \mathfrak g\longrightarrow \mathfrak g,\quad (x,y)\longmapsto [x,y],](/pictures/dewiki/53/5c8fd4c53fc6b20a613f9af5c5f3e939.png) welche Lie-Klammer genannt wird und den folgenden Bedingungen genügt:
welche Lie-Klammer genannt wird und den folgenden Bedingungen genügt:- Sie ist bilinear, das heißt linear in beiden Argumenten. Es gilt somit [ax + by,z] = a[x,z] + b[y,z] und [z,ax + by] = a[z,x] + b[z,y] für alle
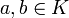 und alle
und alle 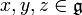 .
. - Sie genügt der Jacobi-Identität. Die Jacobi-Identität lautet: [x,[y,z]] + [y,[z,x]] + [z,[x,y]] = 0 gilt für alle
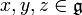 .
. - Es gilt [x,x] = 0 für alle
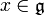 .
.
Die erste und dritte Eigenschaft implizieren zusammengenommen die Antisymmetrie [x,y] = − [y,x] für alle
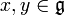 .
.Wenn der Körper K nicht Charakteristik 2 hat, so kann man aus der Antisymmetrie alleine wieder die dritte Eigenschaft herleiten (man wähle y = x).
Lie-Klammern sind im Allgemeinen nicht assoziativ: [[x,y],z] muss nicht gleich [x,[y,z]] sein.
Anstelle eines Körpers und eines Vektorraums lässt sich eine Lie-Algebra allgemeiner für einen kommutativen unitären Ring definieren.
Beispiele
Aus der Algebra
- Man kann jede assoziative Algebra A zu einer Lie-Algebra machen, indem man als Lie-Klammer den Kommutator
-
- wählt. Umgekehrt kann man zeigen, dass sich jede Lie-Algebra als eingebettet in eine assoziative Algebra mit einem Kommutator auffassen lässt, die so genannte universelle einhüllende Algebra.
- Die allgemeine lineare Lie-Algebra
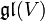 für einen K-Vektorraum V ist die Lie-Algebra der Endomorphismen von V mit dem Kommutator
für einen K-Vektorraum V ist die Lie-Algebra der Endomorphismen von V mit dem Kommutator
-
- [A,B] = AB − BA
- als Lie-Klammer. Ist speziell V = Kn, so schreibt man
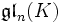 statt
statt 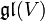 .
.
- Ein Ideal in
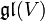 wird von den Endomorphismen mit Spur 0 gebildet. Es heißt „spezielle lineare Lie-Algebra“ und wird mit
wird von den Endomorphismen mit Spur 0 gebildet. Es heißt „spezielle lineare Lie-Algebra“ und wird mit 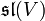 bzw.
bzw. 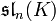 bezeichnet.
bezeichnet. - Der Vektorraum
 bildet eine Lie-Algebra, wenn man die Lie-Klammer als das Kreuzprodukt definiert.
bildet eine Lie-Algebra, wenn man die Lie-Klammer als das Kreuzprodukt definiert. - Als konkretes Beispiel betrachten wir die Lie-Gruppe
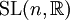 aller
aller 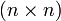 -Matrizen mit reellen Elementen und Determinante 1. Der Tangentialraum der Einheitsmatrix kann mit dem Raum aller reellen
-Matrizen mit reellen Elementen und Determinante 1. Der Tangentialraum der Einheitsmatrix kann mit dem Raum aller reellen 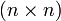 -Matrizen mit Spur 0 identifiziert werden, und die Matrizen-Multiplikation der Lie-Gruppe liefert über den Kommutator die Lie-Klammer der Lie-Algebra.
-Matrizen mit Spur 0 identifiziert werden, und die Matrizen-Multiplikation der Lie-Gruppe liefert über den Kommutator die Lie-Klammer der Lie-Algebra.
Aus der Physik
In der Physik sind die Liegruppen SO(n) bzw. SU(n) wichtig, das sind die Drehungen des reellen bzw. komplexen Raumes in n Dimensionen. Wie schon gesagt, erinnert nicht nur die Bezeichnungsweise für das Lieprodukt an das Kreuzprodukt von Vektoren im Dreidimensionalen, sondern die Gruppeneigenschaft bedeutet hier konkret, dass z. B. das Produkt zweier Drehungen um je eine Achse als Drehung um eine dritte Achse darstellbar sein muss, so dass man auf die Exponentialfunktion geführt wird. In der Tat lassen sich die Gruppen SU(n) in der Form
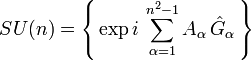 mit komplexen Zahlen Aα darstellen, wobei die selbstadjungierten Operatoren
mit komplexen Zahlen Aα darstellen, wobei die selbstadjungierten Operatoren 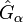 den Elementen der Lie-Algebra entsprechen. Insgesamt erhält man so unitäre Operatoren in einem sog. Hilbert-Raum. Näheres siehe Quantenmechanik, Eichtheorien und Quantenchromodynamik.
den Elementen der Lie-Algebra entsprechen. Insgesamt erhält man so unitäre Operatoren in einem sog. Hilbert-Raum. Näheres siehe Quantenmechanik, Eichtheorien und Quantenchromodynamik.Glatte Vektorfelder
Die glatten Vektorfelder auf einer differenzierbaren Mannigfaltigkeit bilden eine unendlich-dimensionale Lie-Algebra. Die Vektorfelder operieren als Lie-Ableitung auf dem Ring der glatten Funktionen. Seien X,Y zwei glatte Vektorfelder und f eine glatte Funktion. Wir definieren die Lie-Klammer durch
![\ [X, Y]f := (XY - YX)f](/pictures/dewiki/99/cc2a1e9fc21b0a98b2210875d171f3e8.png) .
.
Lie-Algebra einer Lie-Gruppe
Der Vektorraum der linksinvarianten Vektorfelder auf einer Lie-Gruppe ist unter dieser Kommutatoroperation abgeschlossen und bildet eine endlich-dimensionale Lie-Algebra.
Glatte Funktionen mit der Poisson-Klammer
Die glatten Funktionen auf einer symplektischen Mannigfaltigkeit bilden mit der Poisson-Klammer eine Lie-Algebra. Vergleiche Poisson-Mannigfaltigkeit.
Homomorphismen
Seien
 und
und 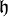 zwei Lie-Algebren. Eine lineare Abbildung
zwei Lie-Algebren. Eine lineare Abbildung  heißt Lie-Algebra-Homomorphismus, wenn
heißt Lie-Algebra-Homomorphismus, wenn ![[\varphi(x),\varphi(y)]=\varphi([x,y])](/pictures/dewiki/102/f78b08ac9e6beb0bef0f6df577b212ad.png) für alle
für alle 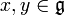 gilt.
gilt.In der Kategorie der Lie-Algebren sind die Lie-Algebren die Objekte und die Lie-Algebra-Homomorphismen die Pfeile.
Unteralgebra
Eine Unteralgebra einer Lie-Algebra
 ist ein Untervektorraum
ist ein Untervektorraum  , der abgeschlossen unter der Lie-Klammer ist. Das heißt, für alle
, der abgeschlossen unter der Lie-Klammer ist. Das heißt, für alle 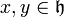 gilt
gilt ![[x,y]\in \mathfrak h](/pictures/dewiki/51/30adca6339293e7c6eec4823005f9426.png) . Eine Unteralgebra ist selbst eine Lie-Algebra.
. Eine Unteralgebra ist selbst eine Lie-Algebra.Ideal
Eine Unteralgebra
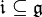 heißt Ideal, wenn
heißt Ideal, wenn ![[x,y]\in \mathfrak i](/pictures/dewiki/49/169ae87e610ca20ade6ebcf3a43bbdd9.png) für alle
für alle 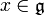 und
und 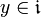 gilt.
gilt.Die Ideale sind genau die Kerne der Lie-Algebra-Homomorphismen.
Auf dem Quotientenraum
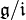 wird durch
wird durch ![[x+\mathfrak i,y+\mathfrak i]:=[x,y]+\mathfrak i](/pictures/dewiki/57/9b4923ba90de7e27414d692bc13cc3b8.png) eine Lie-Algebra definiert, die Quotienten-Algebra. Dabei waren
eine Lie-Algebra definiert, die Quotienten-Algebra. Dabei waren 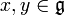 .
.Satz von Ado
Der Satz von Ado (nach dem russischen Mathematiker Igor Dmitrijewitsch Ado) besagt, dass jede endlichdimensionale komplexe Lie-Algebra isomorph zu einer Unteralgebra der
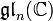 für ein genügend großes n ist. Das heißt, man kann jede endlichdimensionale komplexe Lie-Algebra als eine Lie-Algebra von Matrizen darstellen.
für ein genügend großes n ist. Das heißt, man kann jede endlichdimensionale komplexe Lie-Algebra als eine Lie-Algebra von Matrizen darstellen.Typen von Lie-Algebren
Abelsche Lie-Algebra
Eine Lie-Algebra ist abelsch, wenn die Lie-Klammer identisch Null ist.
Jeder Vektorraum bildet eine abelsche Lie-Algebra, wenn man jede Lie-Klammer als Null definiert.
Nilpotente Lie-Algebra
Sei
 eine Lie-Algebra. Wir definieren die absteigende Zentralreihe durch:
eine Lie-Algebra. Wir definieren die absteigende Zentralreihe durch:![\mathcal C^0\mathfrak g=\mathfrak g,\;\;\;
\mathcal C^1\mathfrak g=[\mathfrak g,\mathfrak g],\;\;\;
\mathcal C^2\mathfrak g=[\mathfrak g,\mathcal C^1\mathfrak g]](/pictures/dewiki/97/a78a869eabb040575822db7950e64f46.png) , allgemein
, allgemein ![\mathcal C^{n+1}\mathfrak g=[\mathfrak g,\mathcal C^n\mathfrak g]](/pictures/dewiki/102/f09137796c5ad133a10cd357c869493b.png) .
.
Die absteigende Zentralreihe wird gelegentlich auch
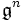 o.ä. geschrieben.
o.ä. geschrieben.Eine Lie-Algebra heißt nilpotent, wenn ihre absteigende Zentralreihe schließlich Null wird, d.h.
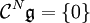 für einen Index N.
für einen Index N.Satz von Engel
Sei
 eine endlichdimensionale komplexe Lie-Algebra, dann sind die beiden folgenden Aussagen äquivalent:
eine endlichdimensionale komplexe Lie-Algebra, dann sind die beiden folgenden Aussagen äquivalent:- Die Lie-Algebra
 ist nilpotent
ist nilpotent - Für jedes
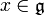 ist
ist ![{\rm ad}(x):\mathfrak g\longrightarrow \mathfrak g,\ y\longmapsto [x,y]](/pictures/dewiki/97/a869fdf64864ca682fe6f678f746ec9b.png) eine nilpotente lineare Abbildung.
eine nilpotente lineare Abbildung.
Auflösbare Lie-Algebra
Sei
 eine Lie-Algebra. Wir definieren die abgeleitete (oder derivierte) Reihe durch:
eine Lie-Algebra. Wir definieren die abgeleitete (oder derivierte) Reihe durch:![\mathcal D^0\mathfrak g=\mathfrak g,\;\;\; \mathcal D\mathfrak g=[\mathfrak g,\mathfrak g],
\;\;\; \mathcal D^2\mathfrak g=[\mathcal D\mathfrak g,\mathcal D\mathfrak g]](/pictures/dewiki/54/607cbdbec329c15402742f4fddd38e9c.png) , allgemein
, allgemein ![\mathcal D^{n+1}\mathfrak g=[\mathcal D^n\mathfrak g,\mathcal D^n\mathfrak g]](/pictures/dewiki/102/f3117b62f06fe28f1b9cc40278cba153.png) .
.
Die abgeleitete Reihe wird gelegentlich auch
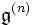 o.ä. geschrieben.
o.ä. geschrieben.Eine Lie-Algebra heißt auflösbar, wenn ihre abgeleitete Reihe schließlich Null wird, d.h.
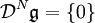 für große N.
für große N.Eine maximale auflösbare Unteralgebra heißt Borel-Unteralgebra.
Einfache Lie-Algebra
Eine Lie-Algebra heißt einfach, wenn sie kein nicht-triviales Ideal hat und nicht abelsch ist.
Bei den Lie-Algebren wird Einfachheit abweichend verwendet. Dies kann zu Verwirrungen führen. Wenn man eine Lie-Algebra als algebraische Struktur auffasst, so ist die Forderung, dass sie nicht abelsch sein darf, unnatürlich.
Halbeinfache Lie-Algebra
Eine Lie-Algebra
 heißt halbeinfach, wenn sie die direkte Summe von einfachen Lie-Algebren ist.
heißt halbeinfach, wenn sie die direkte Summe von einfachen Lie-Algebren ist.Für eine endlichdimensionale Lie-Algebra g sind die folgenden Aussagen äquivalent:
 ist halbeinfach.
ist halbeinfach.- Das Radikal von
 verschwindet.
verschwindet. - Die Killing-Form:
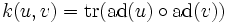 ist nicht entartet (tr bezeichnet die Spur von Endomorphismen).
ist nicht entartet (tr bezeichnet die Spur von Endomorphismen).
Satz von Weyl
Sei
 eine halbeinfache, endlichdimensionale, komplexe Lie-Algebra, dann ist jede endlichdimensionale Darstellung von
eine halbeinfache, endlichdimensionale, komplexe Lie-Algebra, dann ist jede endlichdimensionale Darstellung von  vollständig reduzibel.
vollständig reduzibel.Klassifikation
Halbeinfache komplexe Lie-Algebren können anhand ihrer Wurzelsysteme klassifiziert werden; diese Klassifikation wurde 1900 von Élie Cartan abgeschlossen.
Reelle Lie-Algebren
Eine Auswahl reeller Lie-Algebren
- 1-dimensionale:
- 2-dimensionale:
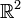
- [a,b] = a
- 3-dimensionale:
- 4-dimensionale:
- Basis {U,X,Y,Z} mit [U,X] = Y,[U,Y] = Z,[X,Y] = 0, Z im Zentrum, ist nilpotent mit Nilindex 3. Diese heißt Filiform-Lie-Algebra.
- 5-dimensionale:
- 6-dimensionale:
Literatur
- Igor Frenkel, James Lepowsky, Arne Meurman: Vertex Operator Algebras and the Monster, Academic Press, New York (1989) ISBN 0-12-267065-5
- Anthony W. Knapp: Lie Groups Beyond an Introduction, Birkhäuser (2002) ISBN 0-8176-4259-5
- Jean-Pierre Serre: Complex Semisimple Lie Algebras, Springer, Berlin, 2001. ISBN 3-5406-7827-1
Wikimedia Foundation.

![[x,y] = x\cdot y - y\cdot x](/pictures/dewiki/100/d7224ff86672b80d8882e638ee553f39.png)

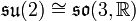
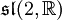
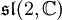
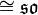 (
(