- Yang-Mills-Gleichungen
-
Die Yang-Mills-Theorie (nach Chen Ning Yang und Robert L. Mills) ist eine nichtabelsche Eichtheorie, die zur Beschreibung der starken und schwachen Wechselwirkung herangezogen wird. Hingegen ist die Elektrodynamik ein Beispiel einer abelschen Eichtheorie.
Dieser Artikel beschreibt vorwiegend die mathematischen Aspekte des Phänomens. Die physikalischen Aspekte werden bei einem der wichtigsten Beispiele für Yang-Mills-Theorien, der Quantenchromodynamik besprochen.
Yang-Mills-Feldenergie
Die Yang-Mills-Theorie geht von der Yang-Mills-Wirkung
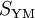 für die Eichbosonen aus:
für die Eichbosonen aus:Die Größe
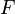 heißt Yang-Mills-Feldstärke;
heißt Yang-Mills-Feldstärke; 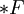 ist die zu F duale Yang-Mills-Feldstärke. Die positive Größe g bedeutet in der Physik die Wechselwirkungskonstante.
ist die zu F duale Yang-Mills-Feldstärke. Die positive Größe g bedeutet in der Physik die Wechselwirkungskonstante.Wendet man jetzt das Prinzip der kleinsten Wirkung auf die durch
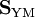 repräsentierten Eichbosonenfelder an, so erhält man als zugehörige Euler-Lagrange-Gleichungen die Yang-Mills-Gleichungen:
repräsentierten Eichbosonenfelder an, so erhält man als zugehörige Euler-Lagrange-Gleichungen die Yang-Mills-Gleichungen: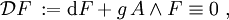 wobei der Term ~g die Yang-Mills-Ladungen enthält.
wobei der Term ~g die Yang-Mills-Ladungen enthält.
Hier wurde die mathematische Sprache der Differentialformen verwendet, die eine kompakte Notierung erlaubt. Die Yang-Mills-Feldstärke ist durch die zweite Maurer-Cartan-Strukturgleichung definiert, die einen Zusammenhang
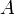 (genauer gesagt dessen lokale Darstellung) eines Hauptfaserbündels (in der Physik Eichpotential bzw. Eichbosonfeld genannt) mit der Krümmung
(genauer gesagt dessen lokale Darstellung) eines Hauptfaserbündels (in der Physik Eichpotential bzw. Eichbosonfeld genannt) mit der Krümmung 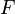 desselben (in der Physik Feldstärke bzw. Feldstärketensor genannt) in Verbindung bringt:
desselben (in der Physik Feldstärke bzw. Feldstärketensor genannt) in Verbindung bringt:Hier ist
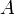 eine liealgebra-wertige 1-Form über dem Hauptfaserbündel und
eine liealgebra-wertige 1-Form über dem Hauptfaserbündel und 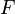 eine liealgebra-wertige 2-Form über diesem Hauptfaserbündel. Ferner stellt
eine liealgebra-wertige 2-Form über diesem Hauptfaserbündel. Ferner stellt 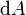 die äußere Ableitung und
die äußere Ableitung und 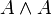 das äußere Produkt von Differentialformen dar (das hier zwischen den A nicht verschwindet, da die Liealgebra-Komponenten von A im Allgemeinen nicht vertauschen). In Komponentenschreibweise, und mit der Kopplungskonstante g, gilt wie in der Quantenchromodynamik
das äußere Produkt von Differentialformen dar (das hier zwischen den A nicht verschwindet, da die Liealgebra-Komponenten von A im Allgemeinen nicht vertauschen). In Komponentenschreibweise, und mit der Kopplungskonstante g, gilt wie in der QuantenchromodynamikDer oben erwähnte Dualitätsoperator * ist bezüglich der Indizes μ und ν mit der Signatur des Minkowskiraums
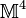 zu bilden, z. B. mit (+---). Bezüglich der Indizes a muss man entsprechend der betrachteten Gruppe vorgehen. Analoges gilt auch für die Spur (Tr ist der englische Ausdruck, eine Abkürzung für "trace"). Obere und untere Indizes, sowie die Reihenfolge von Doppelindizes, werden durch die *-Operation vertauscht. Das Yang-Mills-Funktional kann also auch in der expliziten Form
zu bilden, z. B. mit (+---). Bezüglich der Indizes a muss man entsprechend der betrachteten Gruppe vorgehen. Analoges gilt auch für die Spur (Tr ist der englische Ausdruck, eine Abkürzung für "trace"). Obere und untere Indizes, sowie die Reihenfolge von Doppelindizes, werden durch die *-Operation vertauscht. Das Yang-Mills-Funktional kann also auch in der expliziten Form 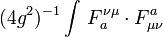 geschrieben werden.
geschrieben werden.In der Physik betrachtet man meist eine kompakte, halbeinfache Liegruppe
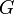 , etwa
, etwa 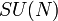 oder
oder 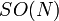 , deren hermitesche Generatoren folgende Kommutationsrelation erfüllen:
, deren hermitesche Generatoren folgende Kommutationsrelation erfüllen:Die
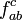 heißen (reelle) Strukturkonstanten der Liegruppe. Ein beliebiges Element U von G wird durch folgende Gleichung dargestellt:
heißen (reelle) Strukturkonstanten der Liegruppe. Ein beliebiges Element U von G wird durch folgende Gleichung dargestellt:Dirac-Teilchen in der Yang-Mills-Theorie
Die Wellenfunktion (Dirac-Feld) ψ eines (mit Yang-Mills-Ladungen) geladenen Teilchens transformiert unter
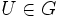 so:
so: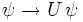 bzw.
bzw. 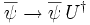
(gilt nur für Teilchen, die nach der fundamentalen Darstellung der Eichgruppe transformieren). Die Lagrange-Funktion für das Dirac-Feld, aus der über die Euler-Lagrangegleichungen die Bewegungsgleichungen des dadurch beschriebenen geladenen Fermion-Teilchens folgen, sieht wegen der Kopplung von Dirac-Feld ψ und Yang-Mills-Feld A („Eichfeld“) wie folgt aus:
wobei g die oben angegebene Kopplungskonstante ist. Diese Lagrange-Funktion beschreibt die Kopplung des Feldes A an die Materie-Felder ψ. Der Ausdruck
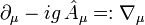 wird kovariante Ableitung oder minimale Kopplung genannt. Die Variablen
wird kovariante Ableitung oder minimale Kopplung genannt. Die Variablen 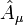 bilden die Vierervektor-Komponenten der zusätzlich noch Liealgebra-wertigen 1-Form
bilden die Vierervektor-Komponenten der zusätzlich noch Liealgebra-wertigen 1-Form 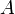 (d. h., die Indizes a sind zur Vereinfachung weggelassen; meist läßt man auch das Symbol ^ weg, was hier der Deutlichkeit halber bei der kovarianten Ableitung nicht geschieht). Natürlich kommt auch bei Berücksichtigung von Dirac-Teilchen in der Gesamtwirkung noch der oben erwähnte Feld-Anteil hinzu, der hier durch die Punkte angedeutet ist und nicht explizit von ψ abhängt.
(d. h., die Indizes a sind zur Vereinfachung weggelassen; meist läßt man auch das Symbol ^ weg, was hier der Deutlichkeit halber bei der kovarianten Ableitung nicht geschieht). Natürlich kommt auch bei Berücksichtigung von Dirac-Teilchen in der Gesamtwirkung noch der oben erwähnte Feld-Anteil hinzu, der hier durch die Punkte angedeutet ist und nicht explizit von ψ abhängt.Wenn die Yang-Mills-Theorie zur Beschreibung der starken Wechselwirkung eingesetzt wird (und zwar in Form einer
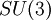 -Eichtheorie, der schon erwähnten Quantenchromodynamik), dann beschreibt
-Eichtheorie, der schon erwähnten Quantenchromodynamik), dann beschreibt 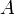 das sog. Gluonfeld, und zwar stellen die
das sog. Gluonfeld, und zwar stellen die 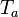 die acht Gluonenarten dar (die
die acht Gluonenarten dar (die 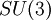 hat 8 Generatoren, üblicherweise verwendet man die sog. Gell-Mann-Matrizen). Einige wichtige Yang-Mills Theorien mit geladenen Fermionen-Materiefeldern besitzen die Eigenschaft der sog. asymptotischen Freiheit bei hohen Energien bzw. kurzen Abständen, was von der Eichgruppe und der Anzahl der Fermionentypen abhängt.
hat 8 Generatoren, üblicherweise verwendet man die sog. Gell-Mann-Matrizen). Einige wichtige Yang-Mills Theorien mit geladenen Fermionen-Materiefeldern besitzen die Eigenschaft der sog. asymptotischen Freiheit bei hohen Energien bzw. kurzen Abständen, was von der Eichgruppe und der Anzahl der Fermionentypen abhängt.Offene Probleme
Ein großer Fortschritt in der Durchsetzung der Yang-Mills-Theorien in der Physik ist der Nachweis ihrer Renormierbarkeit durch Gerardus ’t Hooft Anfang der 1970er Jahre. Die Renormierbarkeit gilt auch, wenn die Eichbosonen massiv sind wie in der elektroschwachen Wechselwirkung. Die Massen werden nach dem Standardmodell durch den sog. Higgs-Mechanismus erworben.
In der Mathematik ist die Yang-Mills-Theorie aktuelles Forschungsgebiet und diente z. B. Simon Donaldson zur Klassifikation differenzierbarer Strukturen auf 4-Mannigfaltigkeiten. Die Theorie wurde vom Clay Mathematics Institute in die Liste der Millennium-Probleme aufgenommen. Insbesondere geht es bei diesem Preis-Problem darum nachzuweisen, dass die niedrigsten Anregungen einer reinen Yang-Mills Theorie (das heißt ohne Materiefelder) eine endliche Masse bzw. Anregungsenergie haben (das heißt, es besteht ein Mass-Gap zum Vakuumzustand). Ein damit zusammenhängendes weiteres offenes Problem ist der Nachweis der vermuteten Confinement-Eigenschaft von Yang-Mills-Feldern in Wechselwirkung mit Fermionenfeldern.
In der Physik erfolgen die Untersuchung von Yang-Mills-Theorien inzwischen nicht über störungstheoretische oder analytische Methoden, sondern meist über Gitterrechnungen (Gitter-Eichtheorien).
Wikimedia Foundation.

![\mathbf S_\mathrm{YM} = \frac{1}{4g^2}\int \operatorname{Tr}\left[ *F\wedge F \right]\,.](/pictures/dewiki/51/3efca72c8635f25cd2709d12f0684251.png)
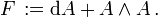
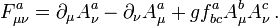
![\left[ T_a, T_b \right] = i f_{ab}^c \, T_c\,.](/pictures/dewiki/101/e31ee146d8c01bd90dc0bad532d10b76.png)
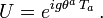
![\mathcal{L}(\psi ,A) := \overline{\psi}\, \left[ i\, \gamma^\mu \left( \partial_\mu - i g\, \hat A_\mu \right) + m \right] \psi +\dots\,,](/pictures/dewiki/52/45647fd57c7017067563688f279339a8.png)