Zerfallskonstante

Der Begriff Lebensdauer kennzeichnet in der Physik die mittlere Lebenszeit eines Mitgliedes eines Ensembles identischer Objekte. Die Lebenszeit jedes Objektes folgt dabei einer vorgegebenen Wahrscheinlichkeitsverteilung, deren Mittelwert die Lebensdauer ist. Sie ist damit eine statistisch definierte Größe.

Typischerweise spricht man von Lebensdauer im Zusammenhang mit instabilen Teilchen, z. B. radioaktiven Atomkernen, oder Systemen in einem angeregten Zustand. Die Wahrscheinlichkeitsdichte dafür, dass ein Mitglied des Ensembles zerfällt, folgt in der Regel einer Exponentialverteilung:

P(t) = αe ^{− λt},

wobei λ die Zerfallskonstante ist (siehe auch exponentielles Wachstum). Die Lebensdauer τ ist mit der Zerfallskonstante über die Relation

τ = 1 / λ

verknüpft. Sie gibt die Zeit an, nach der die Anzahl der Teilchen auf den Bruchteil 1 / e abgefallen ist.

Manchmal findet statt der Lebensdauer der Begriff der Halbwertszeit T_{1 / 2} Verwendung, d. h. die Zeit, in welcher die Hälfte des Ensembles zerfallen ist. Die Halbwertszeit errechnet sich aus der Lebensdauer mit Hilfe von

T_{1 / 2} = τln2.

Verbindung mit der Quantentheorie

Durch die heisenbergsche Unschärferelation lässt sich folgender Zusammenhang zwischen der Unschärfe einer beliebigen Observablen A und ihrer zeitlichen Entwicklung finden:

$\Delta E\ \Delta A \ge \frac{1}{2} \left| \langle [ H, A ] \rangle \right| \ge \frac{\hbar}{2}\left| \frac{\mathrm d}{\mathrm dt} \langle A \rangle \right|$

Dadurch lässt sich eine Verbindung zwischen der Energieunschärfe und der Lebensdauer finden:

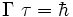$\Gamma\ \tau = \hbar$ mit $\Gamma = 2\ \Delta E$

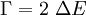
Bei der Bestimmung von Lebensdauern von angeregten Zuständen kann es einfacher sein, experimentell die Energien von z.B. emittierten Photonen in einem Szintillationszähler zu bestimmen, um daraus über die Statistik und die obige Formel die Lebensdauer des Ausgangszustandes zu bestimmen.

Siehe auch

• Lebensdauer (Technik)
• Energie-Zeit-Unschärferelation (zur quantentheoretischen Betrachtung)