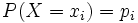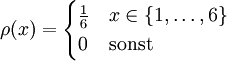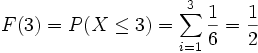Zähldichte

Ein Zufallsexperiment mit endlich oder abzählbar vielen möglichen Ausgängen lässt sich durch eine Wahrscheinlichkeitsfunktion (engl.: Probability Function) beschreiben, welche für jeden Ausgang des Experiments dessen Auftretenswahrscheinlichkeit angibt. Im mathematischen Teilgebiet Stochastik werden Zufallsexperimente durch Zufallsvariablen modelliert, deren zufälliger (numerischer) Wert als die Ausprägung eines bestimmten zufälligen Merkmals interpretiert und bezeichnet wird.

Die Wahrscheinlichkeitsfunktion gibt dann die Auftretenswahrscheinlichkeiten der einzelnen Ausprägungen des von einer diskreten Zufallsvariablen modellierten Merkmals an.

Sie ist das Gegenstück zur Dichtefunktion bei stetigen Zufallsvariablen und wird in der Statistik deswegen auch als Zähldichte bezeichnet.

Die Verteilungsfunktion kumuliert die Zähldichten durch Summenbildung.

Wahrscheinlichkeitsfunktion

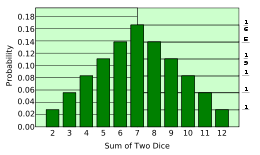Wahrscheinlichkeitsfunktion der Würfelwürfe mit zwei Würfeln (Stabdiagramm):
→ Die Augen sind das Merkmal
→ Deren Anzahl ist die Merkmalsausprägung
→ Die Funktion gibt die Wahrscheinlichkeit des Auftretens einer bestimmten Ausprägung

Eine diskrete Zufallsvariable X nimmt endlich oder abzählbar unendlich viele Werte x_i an. Jedem dieser Werte kann eine Wahrscheinlichkeit $\rho(x_i) = p_i \in [0,1]$ zugeordnet werden, mit der die Zufallsvariable diesen Wert annimmt (mit der sie „mit dieser Ausprägung des Merkmals auftritt“).

Die Wahrscheinlichkeitsverteilung ist dann durch

$P(X=x_i) = p_i\,$

gegeben.

Die Summe der Wahrscheinlichkeiten 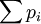$\sum p_i$ muss 1 ergeben, das entspricht der Forderung, dass alle möglichen Ausprägungen x_i berücksichtigt wurden.

Die Wahrscheinlichkeitsfunktion ρ ist mathematisch gesehen die Dichte der Verteilung von X bezüglich des Zählmaßes auf der Menge der möglichen Werte. Ihre Werte werden daher auch als Zähldichte bezeichnet.

Verteilungsfunktion

Die (kumulative) Verteilungsfunktion berechnet sich zu

$F(x) = P(X \leq x) = \sum_{i} p_i$,

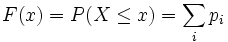wobei der Index i der Summe alle Zahlen 1,2,... durchläuft, für die 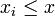$x_i \leq x$ ist.

Beispiel

Die Zufallsvariable X sei das Ergebnis beim Würfeln. Die Verteilung von X ist gegeben durch die Wahrscheinlichkeitsfunktion

$\rho(x) = \begin{cases}{1 \over 6} & x \in \{1, \ldots, 6\} \\ 0 & \mbox{sonst} \end{cases}$

• Die Wahrscheinlichkeit, eine Sechs zu würfeln, ist P(X = 6) = ρ(6) = 1 / 6
• Die Wahrscheinlichkeit, als höchste Augenzahl eine Drei zu würfeln, lässt sich aus der Verteilungsfunktion ablesen:

$F(3) = P(X \leq 3) = \sum_{i=1}^3 {1 \over 6} = {1 \over 2}$