- Liste univariater Wahrscheinlichkeitsverteilungen
-
Diese Liste univariater Wahrscheinlichkeitsverteilungen gibt einen Überblick über die bekanntesten univariaten (eindimensionalen) Wahrscheinlichkeitsverteilungen.
Wahrscheinlichkeitsverteilungen beschreiben, wie sich die Wahrscheinlichkeiten auf die möglichen Ergebnisse einer Zufallsvariable verteilen. Dabei unterscheidet man zwischen diskreten Verteilungen, die auf einer endlichen oder abzählbaren Menge definiert sind, und stetigen (kontinuierlichen) Verteilungen, die meist auf Intervallen definiert sind.
Diskrete Verteilungen lassen sich durch ihre Zähldichte beschreiben. Diese gibt für jeden der maximal abzählbar vielen Werte x einer Zufallsvariablen X die Wahrscheinlichkeit an, dass man genau diesen Wert erhält.
Bei stetigen Verteilungen lassen sich die Wahrscheinlichkeiten einzelner Werte nicht angeben, da diese stets die Wahrscheinlichkeit 0 besitzen. Es ist jedoch oft möglich, die Wahrscheinlichkeit, dass eine Zufallsvariable X einen Wert in einem Intervall [a,b] annimmt, als Integral über eine Dichtefunktion (oder Wahrscheinlichkeitsdichte) f(x) darzustellen:
Bei den in dieser Liste aufgenommenen stetigen Verteilungen ist eine solche Darstellung über eine Dichtefunktion möglich.
Diskrete Verteilungen
Die unten stehenden Tabellen fassen die Kenngrößen Träger, Wahrscheinlichkeitsfunktion, Verteilungsfunktion, Erwartungswert und Varianz der folgenden diskreten Verteilungen zusammen:
- Diskrete Gleichverteilung
- Bernoulli-Verteilung (Null-Eins-Verteilung)
- Binomialverteilung
- Negative Binomialverteilung (Pascal-Verteilung)
- Geometrische Verteilung
- Hypergeometrische Verteilung
- Poisson-Verteilung
- Logarithmische Verteilung
Es bezeichne
 die Aufrundungsfunktion,
die Aufrundungsfunktion,  die Abrundungsfunktion und X jeweils eine entsprechend verteilte Zufallsvariable.
die Abrundungsfunktion und X jeweils eine entsprechend verteilte Zufallsvariable.Diskrete Gleichverteilung
Wertebereich der Parameter:  ,
, 
Bild der Wahrscheinlichkeitsfunktion:
Auf , d.h. n = 20
, d.h. n = 20Ergebnismenge: 
Zähldichte: 
Verteilungsfunktion: 

Erwartungswert: 
Varianz: 
Bernoulli-Verteilung (Null-Eins-Verteilung)
Binomialverteilung
Negative Binomialverteilung (Pascal-Verteilung)
Wertebereich der Parameter:  ,
, ![p \in ]0,1]](7/857e75915a48bdf58371c0a20f4756b5.png)
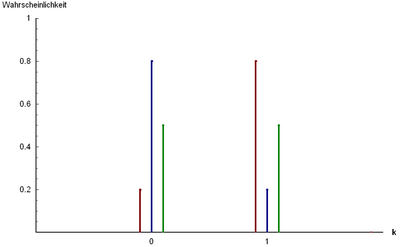
Bild der Wahrscheinlichkeitsfunktion:
r = 10; p = 0.2 (blau), p = 0.5 (grün) und p = 0.8 (rot)Ergebnismenge: 
Zähldichte: 
Verteilungsfunktion: 

Erwartungswert: 
Varianz: 
Geometrische Verteilung
Variante A
Variante B
Hypergeometrische Verteilung
Poisson-Verteilung
Wertebereich der Parameter: 
Bild der Wahrscheinlichkeitsfunktion:
λ = 1 (blau), λ = 5 (grün) und λ = 10 (rot)Ergebnismenge: 
Zähldichte: 
Verteilungsfunktion: 

Erwartungswert: λ Varianz: λ Logarithmische Verteilung
Wertebereich der Parameter: 
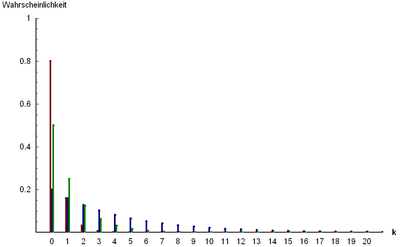
Bild der Wahrscheinlichkeitsfunktion:
p = 0.2 (blau), p = 0.5 (grün) und p = 0.8 (rot)Ergebnismenge: 
Zähldichte: 
Verteilungsfunktion: 

Erwartungswert: 
Varianz: 
Stetige Verteilungen
Die unten stehenden Tabellen fassen die Kenngrößen Träger, Dichtefunktion, Verteilungsfunktion, Erwartungswert und Varianz der folgenden stetigen Verteilungen zusammen:
- Stetige Gleichverteilung (Rechteckverteilung, Uniformverteilung)
- Normalverteilung (Gauß-Verteilung)
- Logarithmische Normalverteilung
- Exponentialverteilung
- Chi-Quadrat-Verteilung (Chi²-Verteilung)
- Studentsche t-Verteilung
- F-Verteilung (Fisher-Verteilung)
- Gammaverteilung
- Betaverteilung
- Logistische Verteilung
- Weibull-Verteilung
- Cauchy-Verteilung (Cauchy-Lorentz-Verteilung, Lorentz-Verteilung)
- Pareto-Verteilung
Dabei bezeichnen Γ(r) die Gammafunktion, B(p,q) die Betafunktion und X jeweils eine entsprechend verteilte Zufallsvariable mit Dichte f(x) und Verteilungsfunktion F(x).
Stetige Gleichverteilung (Rechteckverteilung, Uniformverteilung)
Normalverteilung (Gauß-Verteilung)
Logarithmische Normalverteilung (Log-Normalverteilung)
Exponentialverteilung
Chi-Quadrat-Verteilung (Chi²-Verteilung)
Studentsche t-Verteilung
Wertebereich der Parameter: 
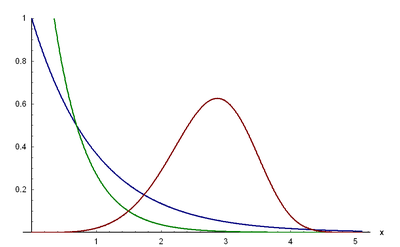
Bild der Dichtefunktion:
k = 2 (blau), k = 5 (grün) und k = 10 (rot)Ergebnismenge: 
Dichtefunktion: 
Verteilungsfunktion: 
Erwartungswert: 0 Varianz: 
F-Verteilung (Fisher-Verteilung)
Gammaverteilung
Betaverteilung
Logistische Verteilung
Wertebereich der Parameter:  und
und 
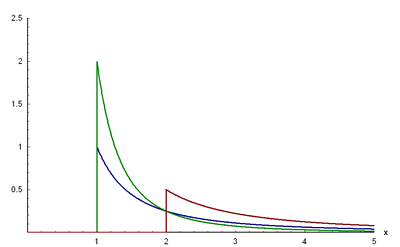
Bild der Dichtefunktion:
α = 0,β = 1 (blau), α = 0,β = 2 (grün) und α = − 1,β = 1 (rot)Ergebnismenge: 
Dichtefunktion: 
Verteilungsfunktion: 
Erwartungswert: α Varianz: 
Weibull-Verteilung
Cauchy-Verteilung (Cauchy-Lorentz-Verteilung, Lorentz-Verteilung)
Pareto-Verteilung
Siehe auch
Weblinks
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta -
Wikimedia Foundation.



![p \in [0,1]](0/550abf67410399d394e58560a62f657a.png)


 1 \
1 \ ,
, 





![p \in ]0,1[](7/2d72164062efcbdfde4e3bd92f4ac888.png)








 ,
, 
 ,
, 












 b
\
b
\










 0
\
0
\



 0
\
0
\



 0
\
0
\



 0
\
0
\ (
( (
(



 0
\
0
\




 1
\
1
\



 0\\
0\\












 1\\
\
1\\
\ 2 \\
\
2 \\
\