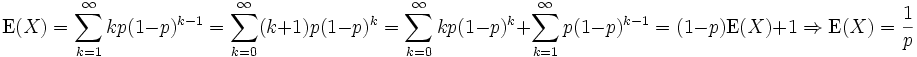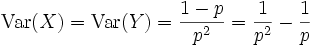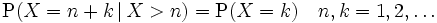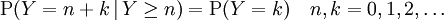- Geometrische-Verteilung
-
Die geometrische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung für unabhängige Bernoulli-Experimente. Es werden zwei Varianten definiert:
- Variante A
- die Wahrscheinlichkeitsverteilung der Anzahl X der Bernoulli-Versuche, die notwendig sind, um einen Erfolg zu haben. Diese Verteilung ist auf der Menge
 definiert.
definiert.
- Variante B
- die Wahrscheinlichkeitsverteilung der Anzahl Y der Fehlversuche vor dem ersten Erfolg. Diese Verteilung ist auf der Menge
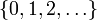 definiert.
definiert.
Die beiden Varianten stehen in der Beziehung X = Y + 1. Welche davon man „geometrische Verteilung“ nennt, wird entweder vorher festgelegt oder man wählt diejenige, die gerade zweckmäßiger ist.
Die geometrische Verteilung wird verwendet:
- bei der Analyse der Wartezeiten bis zum Eintreffen eines bestimmten Ereignisses.
-
- bei der Lebensdauerbestimmung von Geräten und Bauteilen, d.h. dem Warten bis zum ersten Ausfall
- bei der Bestimmung der Anzahl häufiger Ereignisse zwischen unmittelbar aufeinanderfolgenden seltenen Ereignissen wie z.B Fehlern:
-
- Bestimmung der Zuverlässigkeit von Geräten (MTBF)
- Bestimmung des Risikos in der Versicherungsmathematik
- Bestimmung der Fehlerrate in der Datenübertragung, z.B. Anzahl der erfolgreich übertragenen TCP Pakete zwischen zwei Paketen mit Retransmission
Inhaltsverzeichnis
Definition der geometrischen Verteilung
Eine diskrete Zufallsgröße X oder Y mit dem Parameter p (Wahrscheinlichkeit für einen Erfolg), q = 1 − p (Wahrscheinlichkeit für einen Misserfolg) genügt der geometrischen Verteilung G(p), wenn:
- Variante A
- - sie die Wahrscheinlichkeit besitzt, dass man genau n Versuche benötigt, um zum ersten Erfolg zu kommen, zu
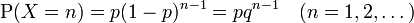
- Variante B
- - sie die Wahrscheinlichkeit besitzt, n Fehlversuche vor dem ersten Erfolg zu haben, zu
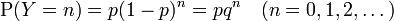
In beiden Fällen bilden die Werte für die Wahrscheinlichkeiten eine geometrische Folge.
Damit besitzt die geometrische Verteilung die folgenden Verteilungsfunktionen
- Variante A
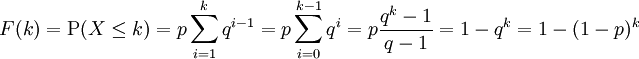
- Variante B
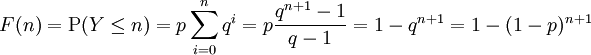
Eigenschaften
Erwartungswert
Die Erwartungswerte der beiden geometrischen Verteilungen sind
- Variante A
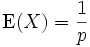
- Variante B
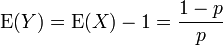 .
.
Der Erwartungswert kann auf verschiedene Weisen hergeleitet werden:
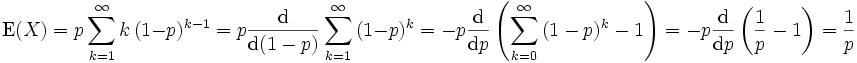 .
.
- Dabei ist
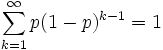 , da p(1 − p)k − 1 die Zähldichte ist.
, da p(1 − p)k − 1 die Zähldichte ist.
- Der Erwartungswert
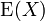 lässt sich per Fallunterscheidung zerlegen. Mit Wahrscheinlichkeit p geht das erste Experiment erfolgreich aus, das heißt, X wird mit 1 realisiert. Mit Wahrscheinlichkeit 1 − p ist das erste Experiment erfolglos, aber der Erwartungswert für die Anzahl der dann noch folgenden Experimente ist wegen der Gedächtnislosigkeit wiederum E(X). Also gilt
lässt sich per Fallunterscheidung zerlegen. Mit Wahrscheinlichkeit p geht das erste Experiment erfolgreich aus, das heißt, X wird mit 1 realisiert. Mit Wahrscheinlichkeit 1 − p ist das erste Experiment erfolglos, aber der Erwartungswert für die Anzahl der dann noch folgenden Experimente ist wegen der Gedächtnislosigkeit wiederum E(X). Also gilt
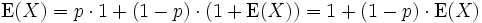 , also
, also 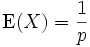
- Führt man n Experimente durch so ist der Erwartungswert für die Anzahl der erfolgreichen Experimente
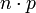 . Daher ist der zu erwartende Abstand zwischen zwei erfolgreichen Experimenten (einschließlich eines erfolgreichen Experimentes)
. Daher ist der zu erwartende Abstand zwischen zwei erfolgreichen Experimenten (einschließlich eines erfolgreichen Experimentes) 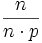 , also
, also 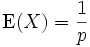 .
.
Varianz
Die Varianzen der beiden geometrischen Verteilungen sind
Die Herleitung kann erfolgen über
-
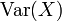
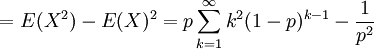
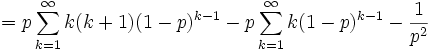
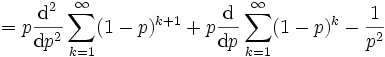
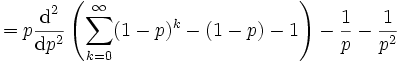
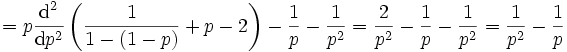 .
.
Gedächtnislosigkeit
Die geometrische Verteilung ist eine gedächtnislose Verteilung, d.h. es gilt für
Variante A
Variante B
Ist also von einer geometrisch verteilten Zufallsvariablen bekannt, dass sie größer als der Wert n ist (Variante A) bzw. mindestens den Wert n hat (Variante B), so ist die Wahrscheinlichkeit, dass sie diesen Wert um k übertrifft genau so groß wie die, dass eine identische Zufallsvariable überhaupt den Wert k annimmt.
Die Gedächtnislosigkeit ist eine definierende Eigenschaft; die geometrische Verteilung ist also die einzig mögliche gedächtnislose diskrete Verteilung. Ihr stetiges Pendant hierbei ist die Exponentialverteilung.
Bezug zur Reproduktivität
Die Summe
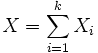 unabhängiger geometrisch verteilter Zufallsgrößen
unabhängiger geometrisch verteilter Zufallsgrößen 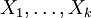 mit demselben Parameter p ist nicht geometrisch verteilt sondern negativ binomialverteilt. Somit ist die Familie der geometrischen Wahrscheinlichkeitsverteilungen nicht reproduktiv.
mit demselben Parameter p ist nicht geometrisch verteilt sondern negativ binomialverteilt. Somit ist die Familie der geometrischen Wahrscheinlichkeitsverteilungen nicht reproduktiv.Schiefe
Die Schiefe ergibt sich zu:
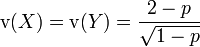 .
.
Wölbung
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
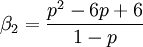 .
.
Charakteristische Funktion
Die charakteristische Funktion hat die Form
- Variante A
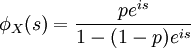 .
.- Variante B
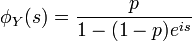 .
.
Momenterzeugende Funktion
Die momenterzeugende Funktion der Geometrischen Verteilung ist
- Variante A
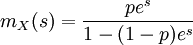
- Variante B
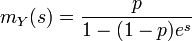 .
.
Beziehungen zu anderen Verteilungen
Beziehung zur negativen Binomialverteilung
- Verallgemeinerung auf mehrere Erfolge
Eine Verallgemeinerung der geometrischen Verteilung stellt die negative Binomialverteilung dar, die die Wahrscheinlichkeit angibt, dass für r Erfolge n Versuche notwendig sind bzw. (in einer alternativen Darstellung) dass der r-te Erfolg eintritt, nachdem bereits k = n − r Misserfolge eingetreten sind.
Umgekehrt ist die Geometrische Verteilung eine negative Binomialverteilung bei r = 1.
Beziehung zur Exponentialverteilung
- Konvergenz der geometrischen Verteilung
Für eine Folge
 geometrisch verteilter Zufallsvariablen mit Parametern
geometrisch verteilter Zufallsvariablen mit Parametern 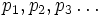 gelte
gelte 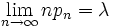 mit einer positiven Konstante λ. Dann konvergiert die Folge
mit einer positiven Konstante λ. Dann konvergiert die Folge 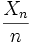 für große n gegen eine exponentialverteilte Zufallsvariable mit Parameter λ.
für große n gegen eine exponentialverteilte Zufallsvariable mit Parameter λ.In Analogie zur diskreten geometrischen Verteilung bestimmt die stetige Exponentialverteilung die Wartezeit bis zum ersten Eintreffen eines seltenen Poisson-verteilten Ereignisses. Die Exponentialverteilung ist also das kontinuierliche Analogon zur diskreten geometrischen Verteilung.
Zufallszahlen
Zufallszahlen zur geometrischen Verteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt. Diese Methode bietet sich bei der geometrischen Verteilung besonders an, da die Einzelwahrscheinlichkeiten der einfachen Rekursion
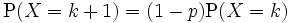 genügen. Die Inversionsmethode ist hier also nur mit rationalen Operationen (Addition, Multiplikation) und ohne die Verteilungsfunktion vorher zu berechnen und abzuspeichern durchführbar, was einen schnellen Algorithmus zur Simulation garantiert.
genügen. Die Inversionsmethode ist hier also nur mit rationalen Operationen (Addition, Multiplikation) und ohne die Verteilungsfunktion vorher zu berechnen und abzuspeichern durchführbar, was einen schnellen Algorithmus zur Simulation garantiert.Weblinks
- Universität Konstanz - Interaktive Animation
- Interaktive Arbeitsblätter zur geometrischen Verteilung auf MathePrisma
- StatWiki Detaillierte Herleitung der momenterzeugenden Funktion
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.