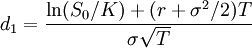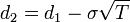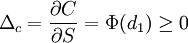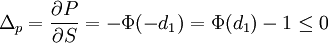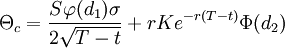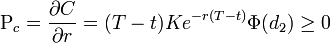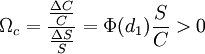Black-Scholes

Das Black-Scholes-Modell ist ein finanzmathematisches Modell zur Bewertung von Finanzoptionen, das von Fischer Black und Myron Samuel Scholes 1973 (nach zweimaliger Ablehnung durch renommierte Zeitschriften) veröffentlicht wurde und als ein Meilenstein der Finanzwirtschaft gilt. Robert C. Merton war ebenfalls an der Ausarbeitung beteiligt, veröffentlichte jedoch einen separaten Artikel. Gerechterweise müsste das Modell daher auch seinen Namen tragen, was sich aber nie durchsetzte. Jedoch wurde Merton zusammen mit Scholes für die Entwicklung dieses Modells mit dem Nobelpreis für Wirtschaftswissenschaften 1997 geehrt, Black war bereits 1995 verstorben. Die Einmaligkeit und Originalität des Modelles von Black, Scholes und Merton ist heute umstritten. Bereits 1908 hatte der Triestiner Mathematiker Vinzenz Bronzin ein weitgehend identisches Modell entwickelt.

Annahmen des Black-Scholes-Modells

Das ursprüngliche Modell trifft einige idealisierte Annahmen:

• Es existiert ein vollkommener und vollständiger Kapitalmarkt. Das bedeutet unter anderem Transaktionskostenfreiheit, keine Beschränkung von Leerverkäufen sowie Arbitragefreiheit.
• Der Kurs der zugrundeliegenden Aktie ist lognormalverteilt. Im Grundmodell werden Aktien betrachtet, die keine Dividenden zahlen.
• Es existiert ein konstanter Zinssatz, zu dem jederzeit beliebig Geld geliehen und angelegt werden kann.

In Modellerweiterungen können auch Dividendenzahlungen, stochastische Zinssätze oder stochastische Volatilitäten betrachtet werden.

Modellrahmen

Das Modell basiert auf der Annahme, dass der natürliche Logarithmus des Basiswertes (also z.B. ein Aktienkurs) S einer Option einem sogenannten Wiener-Prozess folgt, so dass sich die Aktienpreise analog einer geometrischen Brownschen Bewegung verhalten:

dS_t = μS_tdt + σS_tdW_t.

Entwicklung der Dichte des Aktienpreises mit der Zeit

μ ist dabei die erwartete Rendite des Aktienkurses. Über das Argument der risikoneutralen Bewertung beziehungsweise der Arbitragefreiheit geht μ selbst nicht in die Bewertung ein, sondern der risikofreie Zinssatz r. σ bezeichnet die Volatilität, t die Zeit und dW eine zu 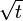$\sqrt{t}$ proportionale, normalverteilte Zufallsgröße. Das Modell nimmt an, dass der Markt Geldanlagen und -aufnahmen zum kontinuierlichen Zinssatz r ohne zusätzliche Kosten (Transaktionskosten) erlaubt.

Ziel ist die Bewertung (Preisbestimmung) eines europäischen Calls C und Puts P auf den Basiswert S mit einem Ausübungspreis K und einer Restlaufzeit von T.

Die Optionen erbringen am Ende der Laufzeit (in T) die Kapitalflüsse:

CF(T,C) = max(S − K;0)

beziehungsweise

CF(T,P) = max(K − S;0)

Black und Scholes zeigen in ihrem Artikel, dass unter der Annahme einer konstanten Zins- und Volatilitätsentwicklung die Option durch ein geeignetes Portfolio bestehend aus dem Basiswert S und einer Anlage oder einem Kredit mit dem Zinssatz r dynamisch dupliziert werden kann. Der Wert der Option muss dann zu jedem Zeitpunkt mit dem Wert des Duplikationsportfolios übereinstimmen.

Der faire Preis der Option kann über verschiedene Argumentationen hergeleitet werden. Er kann als diskontierter Erwartungswert der Auszahlungen in T dargestellt werden, wobei der Erwartungswert bezüglich der Lognormalverteilung zu bilden ist:

C = S₀Φ(d₁) − Ke ^{− rT}Φ(d₂)

P = Ke ^{− rT}Φ( − d₂) − S₀Φ( − d₁)

wobei

$d_1 = \frac{\ln(S_0/K) + (r + \sigma^2/2)T}{\sigma\sqrt{T}}$

$d_2 = d_1 - \sigma\sqrt{T}$

$\Phi(x) = \int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}\exp{\frac{-z^2}{2}}dz$

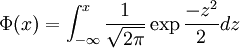
die Verteilungsfunktion der Standardnormalverteilung bezeichnet.

Ein anderer Weg besteht in der Anwendung des Lemmas von Itō und der Annahme der Arbitragefreiheit. Sie führen zu der Black-Scholes Differentialgleichung:

$\frac{\partial V}{\partial t} + rS\frac{\partial V}{\partial S} + \frac{1}{2}\sigma^2S^2\frac{\partial^2V}{\partial S^2}=rV$.

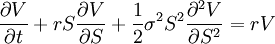V bezeichnet hierbei den Wert einer Option. Diese Differentialgleichung ist unter den gegebenen Annahmen für europäische Aktienoptionen gültig. Nimmt man die Geldflüsse zur Fälligkeit der Option als Anfangswert für die Differentialgleichung, ist die Bewertungsfunktion die Lösung des Anfangswertproblems

Die »Griechen« nach Black-Scholes

Einflussfaktoren

Auf einer ersten Ebene wird der Wert einer Option durch 5 Parameter beeinflusst:

• S₀: Aktueller Aktienkurs, wobei fraglich ist zu welchem Zeitpunkt dieser beobachtet wird
• K: Basispreis ist festgelegt und eindeutig
• r: Zinssatz, neben zeitlichen Unterschieden auch hinsichtlich der Wahl des Zinssatzes gleicher Laufzeit nicht eindeutig
• σ: Die Volatilität ist schwierig zu bestimmen
• T: Zeitkonvention, Gegenstand von Festlegungen

Auf der Zweiten Ebene werden partielle Ableitungen des Optionswertes nach den Faktoren S₀,K,r,σ und T vorgenommen. Auf einer dritten Ebene erfolgt die zweite partielle Ableitung nach dem Aktienkurs S₀. Die zweite und dritte Ebene dieser Betrachtung bezeichnet man auch als „Optionsgriechen“.

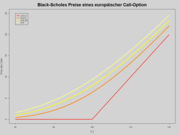
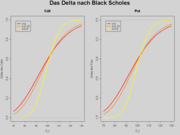
Demonstration der Optionsgriechen anhand der Entwicklung des Callwertes

Als »Griechen« (engl. »Greeks«) werden die partiellen Ableitungen des Optionspreises nach den jeweiligen Modellparametern bezeichnet. Sie helfen Händlern ihr Portfolio auszutarieren, Risiken einzuschätzen und zu kontrollieren.

Preise eines Calls nach Black Scholes

1. Auf der nebenstehenden Grafik sind die Kurven mit europäischen Callwerten unterschiedlicher Restlaufzeit abgetragen. Diese sind überschneidungsfrei und umso höher, je länger die Restlaufzeit ist. Die unterste, geknickte Kurve ist der innere Wert der Option in Abhängigkeit vom aktuellen Basiskurs heute.
2. Die Optionswerte sind monoton wachsend (dies muss nicht allgemein zutreffen, wie etwa bei Zinsoptionen).
3. Der Preis des europäischen Calls liegt immer über seinem inneren Wert. Dies bedeutet ökonomisch, dass es immer besser ist, den Call am Markt zu verkaufen als vorher auszuüben, da der innere Wert (heute) kleiner ist als der Verkaufspreis am Markt. Dies wird im Falle von amerikanischen Calls relevant, da diese ein vorzeitiges Ausübungsrecht besitzen. Generell gilt, dass bei amerikanischen Optionen die vorzeitige Ausübung wertlos ist, solange es sich um ein ertragloses Gut handelt (keine Dividende innerhalb der Optionsfrist).
4. Sensitivität bezüglich Optionspreis: Delta: Steigung der Tangente an Optionswertkurve entspricht dem Delta aus dem Binomialmodell.
   1. at the money (S = E): Das Delta liegt ungefähr bei 1/2. Je größer der Aktienkurs S₀ desto größer die Steigung, das Delta.
   2. deep in the money: Der Optionswert reagiert wie der Aktienkurs selbst.
5. Sensititvität des Deltas bezüglich Optionspreis: Gamma: Das Gamma ist die Krümmung der Kurve, die Konvexität (mathematisch: zweite Ableitung des Callwerts nach dem Aktienkurs)
   1. deep out of the money: Gamma ist nahe Null, d.h. das Delta bleibt konstant.
   2. deep in the money: Gamma ist nahe Null.
6. Sensitivität bezüglich der Laufzeit: Theta: Veränderung des Optionswertes, wenn Kalenderzeit verstreicht. Kurz vor der Fälligkeit ist der Callwert außerordentlich zeitsensititv und besitzt eine hohe Konvexität.
   1. deep out of the money: großer Verlust der Position
   2. at the money: mittlerer Verlust
   3. deep in the money: großer Gewinn

Analog lassen sich entsprechende Beziehungen auch für Putwerte ableiten.

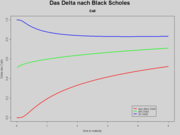
Delta

Delta einer europäischen Option nach Black und Scholes

Delta eines Calls mit der Zeit; jeweils aus, am und im Geld. Für den Put ist der Verlauf genau gleich, nur nach unten verschoben

Das Delta ist die Ableitung des Optionspreises nach dem Preis des Basiswertes. Im Black-Scholes-Modell errechnet man das Delta direkt als:

$\Delta_c = \frac{\partial C}{\partial S}=\Phi(d_1)\ge0$

für den europäischen Call, bzw.

$\Delta_p = \frac{\partial P}{\partial S} = -\Phi(-d_1) = \Phi(d_1)-1\le0$

für den Put. Ein Delta-neutrales Portfolio besitzt ein Delta von Null, es ist daher (lokal; also für kurze Zeiträume) gegen Bewegungen des Basiswertes immun.

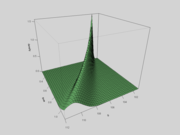
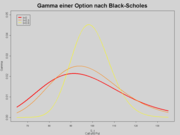
Gamma

Das Gamma ist die zweite Ableitung des Optionspreises nach dem Preis des Basiswertes. Es ist für Call und Put im Black Scholes Modell gleich und zwar

$\Gamma = \frac{\partial^2 C}{\partial S^2} = \frac{\varphi(d_1)}{S\sigma\sqrt{T}} = \frac{\Phi'(d_1)}{S\sigma\sqrt{T}}\ge0$.

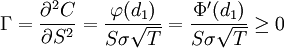Das Gamma ist also immer positiv, das heißt der Optionspreis ändert sich immer in die gleiche Richtung (steigen/fallen) wie die Volatilität. Ist die Option »at the money« (»am Geld«), kann das Gamma bei abnehmender Restlaufzeit über alle Schranken wachsen. Der Buchstabe 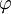$\mathrm{\varphi}$ steht hier für die Dichtefunktion der Normalverteilung, vergl. Φ Verteilungsfunktion.

Gamma einer europäischen Option nach Black Scholes

Vega (Lambda)

Das Vega bezeichnet die Ableitung des Optionspreises nach der Volatilität und gibt somit an, wie stark eine Option auf Änderungen der (im Black-Scholes-Modell konstanten) Volatilität reagiert. Das Vega ist für einen europäischen Call und Put gleich, und zwar

$\Lambda = \frac{\partial C}{\partial \sigma} = \frac{\partial P}{\partial \sigma} = S\varphi(d_1)\sqrt{T-t} = S\Phi'(d_1)\sqrt{T-t}\ge0$.

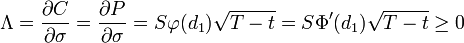Vega ist kein griechischer Buchstabe. Sigma ist als Zeichen schon für die Standardabweichung vergeben, die ja unter anderem als Volatilität interpretiert wird.

Theta

Das Theta bezeichnet die Ableitung nach der Zeit, gibt also die Sensitivität der Option auf Änderungen der Restlaufzeit an. Da sich ceteris paribus mit der Zeit der Wert einer Option an den Payoff zum Fälligkeitsdatum annähert, ist das Theta immer negativ, man verliert mit der Zeit Geld. Es wird auch als Zeitwert der Option bezeichnet. Im Black-Scholes Modell ist es

$\Theta_c = \frac{S\varphi(d_1)\sigma}{2\sqrt{T-t}} + rKe^{-r(T-t)}\Phi(d_2)$

bzw.

$\Theta_p=\frac{S\varphi(d_1)\sigma}{2\sqrt{T-t}} - rKe^{-r(T-t)}\Phi(-d_2)$.

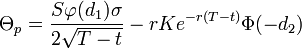Rho

Mit Rho wird die Sensitivität der Option bei kleinen Änderungen des Zinssatzes bezeichnet.

$\Rho_c = \frac{\partial C}{\partial r} = (T - t)Ke^{-r(T - t)}\Phi(d_2)\ge0$

$\Rho_p = \frac{\partial P}{\partial r} = -(T - t)Ke^{-r(T - t)}\Phi(-d_2)\le0$.

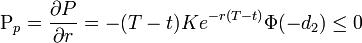Omega

Die Optionselastizität ist eine prozentuale Sensitivität:

$\Omega_c = \frac{\frac{\Delta C}{C}}{\frac{\Delta S}{S}} = \Phi(d_1)\frac{S}{C} >0$

$\Omega_p = \frac{\frac{\Delta P}{P}}{\frac{\Delta S}{S}} = (\Phi(d_1)-1)\frac{S}{P} <0$.

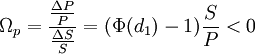Anwendung

Das Delta ist die bedeutendste Optionssensitivität. Wenn man eine Aktie besitzt, so muss das Delta mal die Calloption gleich dem N(x ⁻ ) sein. D.h. bei einem Delta von 1/2, dass zwei Calloptionen so riskant wie eine Aktie sind. Das Delta kann maximal 1 betragen, was bedeutet, dass der Callpreis so wie die Aktie reagiert.

Es ist jedes beliebige Delta über Kauf und Verkauf erzeugbar. Damit kann eine Position bezüglich des Delta (der Aktienkursänderung) abgesichert werden.

Ein Optionshändler, der beispielsweise ein bezüglich des Delta gesichertes Portfolio über das Wochenende hält, hält aber dennoch keine vollkommen risikolose Position, denn über das Wochenende verliert die Position an Zeitwert (Theta). Um diesen Zusammenhang auszunutzen, müssten alle Marktteilnehmer den Titel short (Verkaufen des Titels ohne diesen zu besitzen) gehen. Dies trifft aber nicht zu, da sich die Konvexität (Gamma) in eine andere Richtung bewegt. Der Vorteil der Konvexität (Gamma positiv) ist, dass, wenn der Aktienkurs steigt, dies immer positiv ist. Dies bedeutet aber für denjenigen der den Titel short geht, dass er bei einem steigenden Aktienkurs verliert.

Probleme des Modells

Trotz der berechtigten Kritikpunkte ist die Black-Scholes-Formel aus der Finanzwelt nicht mehr wegzudenken:

1. Die Black-Scholes-Formel steht und fällt mit der Schätzung der Volatilität. Wird zur Berechnung die Implizite Volatilität herangezogen, dann ist das Ergebnis nicht besonders befriedigend. Die Abschätzungsformel nach dem Cox-Ross-Rubinstein-Modell liefert da bessere Ergebnisse.
2. Im Black-Scholes-Modell ist die Volatilität σ konstant. Erweiterte Modelle, in denen die Volatilität als fallende Funktion vom Aktienkurs angenommen werden, wie z.B. das CEV-Modell, liefern bessere Resultate. Marktpreise von Optionen zeigen, dass die (implizite) Volatilität nicht konstant ist, es ist ein Volatilitäts-Smile (volatility smile) zu beobachten. Das liegt daran, dass die sogenannten "Marktpreise" ja auch unter Zuhilfenahme des Black-Scholes-Modells "errechnet" werden. Das Modell geht (mit Ln[Kurs/Basis]) wenig realistisch davon aus, dass der künftige, unterstellte Kurs um den Basiswert streuen würde. Die empirische Erfahrung, die auch von vielen Autoren beobachtet und geteilt wird, zeigt jedoch, dass Kurse eher um den letzten Wert („bester Schätzer“) streuen.

Herleitung des Black-Scholes-Modells

Ausgangspunkt des Black-Scholes-Modells ist das Binomialmodell zur Optionspreisbewertung. Kernidee ist, dass die Handelsintervalle immer kürzer werden

$\Delta t \to 0$.

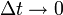u(Δt) und d(Δt) nehmen kontrolliert ab. Die Aktienkursrenditen im diskreten Modell seien binomialverteilt. Sie konvergieren gegen Normalverteilung. Die Aktienkurse sind hingegen in jedem Zeitpunkt logarithmisch normalverteilt. In der Regel ist eine Schrittzahl von 100 ausreichend mit der Einschränkung exotischer Optionen oder Optionssensitivitäten.

Literatur

Originalarbeiten:

• Black, Fischer & Scholes, Myron: The Pricing of Options and Corporate Liabilities Journal of Political Economy 81, 1973, S. 637-654
• Merton, Robert C.: Theory of Rational Option Pricing Bell Journal of Economics and Management Science 4, 1973, S. 141-183

Empirische Kritik:

• Pape, Ulrich/ Merk, Andreas: Zur Angemessenheit von Optionspreisen. Ergebnisse einer empirischen Überprüfung des Black/Scholes-Modells, Working Paper Nr. 4, ESCP-EAP Europäische Wirtschaftshochschule Berlin Dezember 2003

Theoretische Kritik:

• Saber, Nasser: Speculative Capital Financial Times, Prentice Hall 1999
  • Vol. 1. The invisible hand of global finance ISBN 0273641557
  • Vol. 2. The nature of risk in capital markets ISBN 027364422X

Allgemeinverständlich-philosophisch:

• Gerhard Pretting: Traurige Märkte. Die Auflösung der Realität in den Zeichen des Geldes. Warum die Banker den Eindruck erwecken, sie seien jahrelang bei französischen Philosophen in die Schule gegangen in : DIE ZEIT 23. 4. 2009, Nr. 18 (erläutert die Bedeutung des Modells für die Allgemeinheit)

Weblinks

• Nobel-Vorlesungen 1997 von Scholes und Merton
• American Mathematical Society zum 97er Wirtschaftsnobelpreis, mit weiteren Links
• Theorie und Online-Rechner (inkl. VAR und der Greeks) des Black-Scholes Optionsmodels von Jan-Hendrik Dörner, Goethe-Universität, Frankfurt am Main.
• Bradley University mehrseitige, informelle Darstellung mit umfangreicher Bibliographie
• Excel-Makros zur Berechnung des Optionspreises
• Hedge Simulator Zeigt das Ergebnis eines Delta und Delta-Gamma Hedge (Replikation) in diskreter Zeit unter einem Black-Scholes-Modell.
• Online-Rechner Achtung: Web-Oberfläche gut gemacht, sehr instruktiv, aber mangelhafte Numerik
• [1] Basis Black-Scholes Implementierung in diversen Programmiersprachen