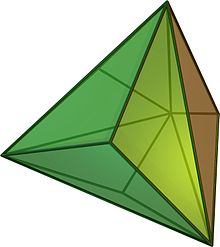
Triakistetraeder

3D-Ansicht eines Triakistetraeders (Animation)

Das Triakistetraeder ist ein konvexes Polyeder, das sich aus zwölf gleichschenkligen Dreiecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum Tetraederstumpf und hat acht Ecken sowie 18 Kanten.

Entstehung

Werden auf alle vier Begrenzungsflächen eines Tetraeders Pyramiden mit der Flankenlänge b aufgesetzt, entsteht ein Triakistetraeder, sofern die Bedingung $\tfrac{a}{3}\sqrt{3}<b<\tfrac{a}{2}\sqrt{2}$ erfüllt ist.

• Für den zuvor genannten minimalen Wert von b haben die aufgesetzten Pyramiden die Höhe 0, sodass lediglich das Tetraeder mit der Kantenlänge a übrig bleibt.

• Das spezielle Triakistetraeder mit gleichen Flächenwinkeln entsteht, wenn $b = \tfrac{3}{5}a$ ist.

• Nimmt b den o. g. maximalen Wert an, entarted das Triakistetraeder zu einem Würfel mit der Kantenlänge b.

• Überschreitet b den maximalen Wert, so ist das Polyeder nicht mehr konvex.

Formeln

Allgemein Größen eines Triakistetraeders mit Kantenlängen a, b Volumen $V = \frac{a^2}{12} \left(a\sqrt{2}+4\sqrt{3b^2-a^2}\right)$ Oberflächeninhalt $O = 3a \sqrt{4b^2-a^2}$ Pyramidenhöhe $k = \frac{1}{3}\sqrt{9b^2-3a^2}$ Inkugelradius $\rho = \frac{a}{12} \sqrt{\frac{48b^2-14a^2+8a\sqrt{6b^2-2a^2}}{4b^2-a^2}}$ Flächenwinkel  (über Kante a) $\cos \, \alpha_1 = \frac{5a^2-12b^2-8a \sqrt{6b^2-2a^2}}{9(4b^2-a^2)}$ Flächenwinkel  (über Kante b) $\cos \, \alpha_2 = \frac{2b^2-a^2}{4b^2-a^2}$

Speziell Größen eines Triakistetraeders mit Kantenlänge a Volumen $V = \frac{3}{20}\,a^3 \sqrt{2}$ Oberflächeninhalt $O = \frac{3}{5}\,a^2 \sqrt{11}$ 2. Seitenlänge $b = \frac{3}{5}\,a$ Pyramidenhöhe $k = \frac{a}{15} \sqrt{6}$ Inkugelradius $\rho = \frac{3}{4}\,a\,\sqrt{\frac{2}{11}}$ Kantenkugelradius $r = \frac{a}{4} \sqrt{2}$ Flächenwinkel  ≈ 129,52° $\cos \, \alpha = -\frac{7}{11}$

Weblinks

• Eric W. Weisstein: Triakistetraeder. In: MathWorld. (englisch)
• Interaktive Darstellung des Triakistetraeders im Mineralienatlas

Platonische Körper

Tetraeder · Würfel · Oktaeder · Dodekaeder · Ikosaeder